42. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента. Что такое “толстые хвосты”?

Инженеры считают, что размеры деталей подчиняются закону нормального распределения (ЗНР), выведенного К.Гауссом

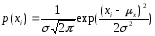
Как видите, в функции Гаусса всего два параметра: математическое ожидание µ_х и стандартное отклонение , которые сравнительно легко оценить по выборке, используя формулы (2.4) и (2.5 ). Эти формулы реализованы в Excel в функциях соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН, категория «Статисти­ческие». Зная параметры гауссианы, можно вычислить процент деталей в различных диапазонах х (квантили), используя таблицы или функцию НОРМРАСП Excel. Поэтому закон нормального распределения широко применяется при проектировании машин и механизмов. Например, можно вычислить количество событий (деталей) в диапазоне {Е(х) -2, Е(х) +2}. Это примерно 95%, то есть в “хвостах” останется по 2,5%. В данном случае р = 0,95 – доверительная вероятность, а {Е(х) -2, Е(х) +2} - соответствующий доверительный интервал.

На Рисунке 2.2 показано применение функции НОРМРАСП. Площадь левого хвоста гауссианы (Рисунок 2.1) от - до -1,96 (почти 2) равна 0,024997895, то есть 2,5%.

В общем виде это утверждение выглядит следующим образом:

для уровня значимости  = 1– р доверительный интервал равен

{Е(х) – t_крит, Е(х) + t_крит}, где t_крит – критические значения статистики Стьюдента t = Е(х)/. В нашем примере  – доля деталей в одном или двух “хвостах”. При уменьшении числа замеров надёжность оценки Е(х) и дисперсии падают, и доверительный интервал надо расширять. Поэтому критические значения статистики Стьюдента зависят от уровня значимости (доверительной вероятности) и количества замеров (степеней свободы). Распределение Стьюдента t_крит(, n) приведено во всех учебниках и практикумах по математической статистике и эконометрике. В Excel имеется функция СТЬЮДРАСП(t_крит, n, число хвостов (1 или 2)), которая возвращает долю событий в одном или двух “хвостах”. Для практических целей достаточно запомнить, что при числе замеров больше 30 и р=95% t_крит примерно равно 2 (при “бесконечном” числе замеров – 1,96).

Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t-статистики Стьюдента. Для b t=b/S_b . Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии  и  лежат в интервалах {a-2S_a , b+2 S_b } и {b-2S_b , b+2 S_a } с доверительной вероятностью 95%.

43.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности

Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр ), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). Множественная линейная регрессионная модель имеет вид: y=a+b1x1+b2x2+…+bpxp+ε Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. быть количественно измеримы. При включении качественного фактора нужно придать ему количественную определенность

2. не должны быть коррелированы между собой и тем более и годиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, когда ryx1 < rx1x2 может повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами

Признаки мультиколлинеарности.

1.В модели с двумя переменными одним из признаков мультиколлинеарности является близкое к единице значение коэффициента парной корреляции. Если значение хотя бы одного из коэффициентов парной корреляции больше, чем 0,8, то мультиколлинеарность представляет собой серьезную проблему. Однако в модели с числом независимых переменных больше двух, парный коэффициент корреляции может принимать небольшое значение даже в случае наличия мультиколлинеарности. В этом случае лучше рассматривать частные коэффициенты корреляции. 2. Для проверки мультиколлинеарности можно рассмотреть детерминант матрицы коэффициентов парной корреляции |r|. Этот детерминант называется детерминантом корреляции |r| ∈(0; 1). Если |r| = 0, то существует полная мультиколлинеарность. Если |r|=1, то мультиколлинеарность отсутствует. Чем ближе |r| к нулю, тем более вероятно наличие мультиколлинеарности. 3. Если оценки имеют большие стандартные ошибки, невысокую значимость, но модель в целом значима (имеет высокий коэффициент детерминации), то это свидетельствует о наличие мультиколлинеарности. 4. Если введение в модель новой независимой переменной приводит к существенному изменению.