lection_part1-2

ласти определяются действующими в ней (гравитационными) полями: силы (геометрия, а именно, отношение между параллельными прямыми, углы между прямыми, углы в треугольнике и т.п.) изменяются при переходе от одной области к другой, в зависимости от концентраций масс в данных областях и их движения.

6.4. Основной закон релятивистской динамики материальной точки

В релятивистской динамике масса тел есть функция их скорости:

где m0 – масса покоя тела (частицы) в ИСО, относительно которой оно покоится (minimum);

m – масса в ИСО, относительно которой оно движется со скоростью v, т.е. масса различна в разных ИСО и с ростом скорости движения u – увеличивается.

В релятивистской динамике основной закон имеет вид ( р– реля-

тивистский импульс):

Уравнение (6.11) внешне совпадает с уравнением классической механики, т.е. инвариантно к преобразованиям Лоренца, тем самым удовлетворяя принципу относительности Эйнштейна. Важно отметить, что ни сила Fr , ни релятивистский импульс p не являются инвариантами. В общем случае вектор силы F не коллинеарен ускорению a . r

Уравнение (6.11) справедливо и для проекций F на координатные

оси Fx, Fy, Fz с учетом формул (6.7), (6.10) для проекций px, py, pz релятиви- r

стского импульса p .

71

В силу однородности и изотропности пространства в релятивистской механике также справедливы законы сохранения релятивистских им-

пульса и момента импульса (в замкнутой системе). Разумеется, вблизи крупных гравитирующих (притягивающих) объектов (см. лекция 7) эти свойства и законы могут нарушаться.

6.5. Закон взаимосвязи массы и энергии. Энергия связи

Найдем выражение для кинетической энергии (КЭ) Т релятивистской

72

При v<<c выражение, стоящее в скобках можно разложить в ряд

Можно показать, что тело обладает не только кинетической, но и энергией покоя.

Полная энергия тела E, согласно А. Эйнштейну, пропорциональ-

В формулу (6.16) не входит потенциальная энергия тела во внешнем силовом поле.

Получим выражение полной энергии как функцию релятивистского импульса (6.11):

энергией покоя.

Для характеристики устойчивости материи (например, устойчи-

вости ядра как системы нуклонов), вводят понятие энергии связи. Энергия связи равна работе, которую надо совершить, чтобы разделить систему на составные части:

где m0i – масса покоя свободной частицы;

М0 – масса покоя системы, состоящей из n частиц;

∆m – называется дефектом массы (масса составляющих больше массы целого).

73

Энергию покоя и дефект масс обычно не учитывают при решении задач в механике, но исторически используют при расчете тепловых эффектов ядерных реакций. Теплота – одна из форм энергии, и закон взаимосвязи массы и энергии (6.16) был полностью подтвержден в экспериментах по определению теплоты, выделяющейся в ядерных реакциях.

6.6. Вывод преобразований Х. Лоренца

Примем как опытный факт, что скорость света в вакууме c не зависит от движения источника света или наблюдателя и одинакова во всех ИСО.

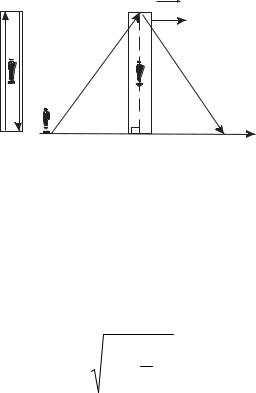
Дана линейка, на одном конце которой находится источник света, дающий очень короткие вспышки, а на другом – зеркало. Пусть линейка расположена перпендикулярно оси Ох и движется со скоростью ur вдоль оси Ох относительно неподвижного наблюдателя (т.е. относительно СО S). СО S1 движется вместе с линейкой и другим наблюдателем (линейка и наблюдатель относительно нее покоится).

Для наблюдателя в СО S1 свет пройдет расстояние 2A1O1=2c∆t1, а для наблюдателя в СО S – 2AO=2c∆t. Так как A1O1=AC<OA, то из условия постоянства скорости света следует, что будет различно время ∆t1 и ∆t. Из ∆OAC по теореме Пифагора:

(т.е. получили случай 1, б) следствий из преобразований Х.Лоренца):

а) если линейка движется, как показано на рис. 6.3 (перпендикулярно оси Ох), то обозначив его длину в СО S l , получают из уравнения (6.20):

74

б) если же стержень движется вдоль в СО S оси Ох с постоянной скоростью ur, то для наблюдателя в СО S при движении света в направлении оси Ох (рис. 6.4): l||+u∆tI=c∆tI, а при движении света обратно (после отражения от зеркала): c∆tII=l||–u∆tII, т.к. ∆t=∆tI +∆tII, то ∆t = c22cl−ΙΙu2 . Для

наблюдателя в СО S1 ∆t1 = 2lcΙΙ1 . То есть, с учетом выражения (6.21) полу-

чают:

(т.е. получили случай 2) следствий из преобразований Х. Лоренца).

Рис. 6.4

Рассмотрим для простоты двумерные системы координат (рис. 6.5), оси которых вначале совпадали. Повернем систему Y1OX1 на угол ϕ относительно YOX как показано на рис. 6.5, тогда:

x1 = OC1 = OD + DC1 =OC cosϕ + BK1 sinϕ = x cosϕ + y sinϕ y1 = OB1 = OK1 − K1B1 = y cosϕ − xsinϕ = −xsinϕ + y cosϕ ,

что удовлетворяет уравнению (6.24).

75

Y1 Y

Рис. 6.5

Если обозначить cosϕ=a, sinϕ=b, то x1=ax+by, y1= – bx+ay, причем a2+b2=1. (6.25)

Если рассматривать сферу радиусом R, то ее уравнение x2+y2+z2=R2. Представим, что в центре сферы расположен источник, а на ее поверхно-

сти – наблюдатель, тогда в СО S x2+y2+z2–c2∆t2=0, а в СО S1:

x12+y12+z12–c2∆t12=0. (6.26)

Если свет распространяется вдоль оси ОХ (параллельной ей оси ОХ1), то с учетом уравнений (6.23) и (6.24) формула имеет вид

y=y1, z=z1. (6.27)

Обобщая двумерный случай (6.24) на четырехмерный случай (6.26) с учетом равенства (6.27):

где Т и Т1 – четвертая координата в этом случае;

i – мнимая единица (i = −1).

Равенство (6.25) справедливо для любой пары координат, поэтому, рассматривая его в терминах x, T и x1, T1, можно записать: x1=ax+bT, T1= – bx+aT, причем a2+b2=1. Так как координаты х, х1 – действительные, то следует положить, что b=id. Тогда, ведя отсчет времени с нуля и обозначая ∆t=t, получают равенство

76

ЛЕКЦИЯ 7. ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

1.Общая теория относительности (ОТО) – релятивистская теория тяготения.

2.Космология и ОТО. Стационарные и нестационарные модели Вселенной.

3.Некоторые следствия из ОТО.

Передизучениемданнойлекцииследует ознакомитьсяслекциями5 и6.

7.1. Общая теория относительности – релятивистская теория тяготения

Строение и развитие Метагалактики (наблюдаемой современными методами радиоастрономии части Вселенной) управляются, в основном, тяготением. ОТО представляет собой теорию тяготения, находящуюся в

согласии с требованием о конечности скорости распространения любых «сигналов», в том числе сил тяготения. Согласно ОТО тяготение проявляется в неэвклидовости (см. ниже) пространства и времени.

Ньютоновская теория всемирного тяготения (НТТ), в которой силы действуют на расстоянии без всякого запаздывания, совершенно очевидным образом не удовлетворяет требованиям частной, специальной теории относительности (СТО). Успех НТТ связан с достаточной точностью для описания движения планет, звезд и даже целых галактик, когда их относительные скорости много меньше скорости света в вакууме c, а разность гравитационных потенциалов много меньше c2. Часто в небесной механике малы поправки, обусловленные запаздыванием и вообще конечностью скорости света. Такое утверждение ясно из следующего сопоставления: свет от Земли до Солнца идет 8 минут, что в 60 000 раз меньше года – времени обращении Земли вокруг Солнца.

Ясно, что ньютоновская теория гравитации – это гравитостати-

ка, аналогом которой является электростатика с ее законом Кулона. Необходимость создания релятивистской теории гравитации (тяготения) была осознана сразу же после возникновения специальной теории относительности (1905г.). Но задача оказалась очень сложной, и построение релятивистской теории тяготения – ОТО (1916г.) – заняло у А. Эйнштейна почти 10 лет (многие ученые считают датой рождения ОТО выход в свет статьи А. Эйнштейна «О принципе относительности и его следствиях» – 1907г.). Дело здесь в том, что можно предложить несколько теорий тяготения, удовлетворяющих требованиям СТО. Действительности же отвечает лишь одна. Конечно, как и всегда в естествознании верная теория может быть отобрана из сравнения выводов теорий с опытом и наблюдениями. Но да-

78

же наблюдений (не говоря уже об опытах) тогда еще не было сделано в силу несовершенства техники (средств измерений). Некоторые следствия из ОТО невозможно проверить и сейчас – после выхода человека в космос, например, существование «черных дыр».

Размышления о свойствах движения в инерциальных системах отсчета (ИСО) и неИСО привели А. Эйнштейна к мысли о независимости движении тел в поле сил инерции от их массы, что наблюдается и в гравитационном поле, и формулированию одного из важнейших принципов фи-

зики – принципа эквивалентности, лежащего в основе ОТО: свойства движения в неИСО такие же, как и в ИСО при наличии гравитационного поля, (т.е. поля сил инерционных и гравитационных эквивалентны – равноускоренная СО эквивалентна однородному гравитационному полю. Естественно предположить (это и было сделано А. Эйнштейном), что подобная эквивалентность имеет место для всех физических явлений и процессов, а не только для механических движений.

Если однородное и постоянное поле тяготения влияет на все физические процессы совершенно так же, как равномерное ускорение систем отсчета, то и произвольное поле тяготения можно связать с геометрией и кинематикой. В пределах достаточно малой области пространства и в течение достаточно небольшого интервала времени любое поле тяготения можно считать однородным и постоянным. Поэтому в любой малой про- странственно-временной области поле тяготения можно «исключить» (т. е. устранить его действие) выбором ускоренной СО – неИСО.

Представив себе как бы «жидкую» СО, ускорение которой в разных точках различно, можно исключить и более сложные поля тяготения. Это не значит, однако, что любое поле тяготения можно «навсегда» ликвидировать выбором СО. Например, поле тяжести Земли направлено к ее центру и может быть на некоторое время исключено, если выбрать свободно падающую на центр Земли СО. Но совершенно очевидно, что использование такой свободно падающей СО ограничено во времени. Следовательно, речь идет не о том, чтобы полностью «свести» поле тяжести к выбору СО. Можно лишь видеть, что поле тяготения полностью характеризуется величинами, определяющими свойства пространства и времени. Таких величин 10, и они в совокупности называются метрическим тензором и обозначаются символом gik. Смысл записи gik таков: индексы i и k соответствуют координатам x, у и z и времени t, причем обычно устанавливают такое соответствие: t – индекс 0, х – индекс 1, у – индекс 2, z – индекс 3. Величины g10 и g01 и аналогичные равны между собой, и, таким образом, всего из 16 возможных имеется именно 10 независимых величин: g00, g11, g22, g33, g10, g20, g30, g12, g13, g23, которые и можно записать в символической форме gik. При переходе от одной СО пространственных координат и времени к другой изменяются как сами координаты х, у, z и t, так и величины gik.

79

Существуют, однако, другие величины, которые не зависят от СО или, как говорят, являются инвариантными, например, пространственновременной интервал. В ОТО (ds)2=∑gikdxidxk при i, k = 0 относится к времени так, что cdt=dx0.

Поясним сказанное выше на примере плоскости (двумерное пространство), на которой находятся две близкие точки. Расстояние между этими точками ∆r не зависит от выбора системы координат на плоскости. В наиболее привычных нам прямоугольных (декартовых) координатах х и у имеем (∆r)2=(∆x)2+(∆y)2, где ∆x и ∆y – разности координат х и у для рассматриваемых точек. В произвольной же системе координат х' и у' на той

же плоскости (∆r)2=g11(∆x')2+2g12∆x' ∆y'+g22(∆y')2. Для трехмерного пространства – (координаты х, у, z) – и четырехмерного пространства-времени –

координаты х, у, z и t (термин пространство-время ввел нем. физик и математик Г. Минковский (1864–1909) в статье «Пространство и время» в 1908г.) ситуация аналогична. С помощью величин gik можно выразить все свойства пространства-времени, в частности, определить расстояния (про- странственно-временной интервал) между любыми событиями.

Итак, в ОТО поле тяготения описывается величинами gik, которые в известном смысле приходят на смену одной величине – ньютоновскому

потенциалу ϕ (см. лекцию 5, вопрос 1). Поле тяготения называется слабым, если потенциал ϕ мал по сравнению с величиной с2 (или, что одно и то же,

скорость тел, движущихся в поле с потенциалом ϕ, мала по сравнению со скоростью света с). Если нет никаких тел (практически на большом расстоянии от всех массивных тел), то можно ввести ИСО, в которой g11=g22=g33 =–1, g00=1, а все остальные gik=0. Помещая в эту СО некоторое невращающееся тело (например, звезду), создающее слабое поле тяготе-

ния, будем иметь g11=g22=g33=–1, g12=g23=g10=g20=g30=0 и g00=1+2ϕ/c2.

В гравитационных полях отдельных небесных тел, например звезд и планет, обычно можно выбрать систему координат так, чтобы наиболее существенной оказалась величина g00, т. е. коэффициент перед (dt)2:

где М – масса гравитирующего тела; R – расстояние до его центра.

Таким образом, мы фактически возвращаемся к НТТ. Даже на поверх-

радиус Солнца r0=6,96 108 м), т.е. величина g00→1 и ньютоновское приближение (НТТ) оказывается хорошим. Но все же отклонения от НТТ можно наблюдать уже в пределах солнечной системы. А. Эйнштейн указал на три

80