
lection_part1-2
.pdf
лярные, проходящие через центр инерции (масс) тела, оси, которые мо-
гут служить свободными осями – они называются главными осями инерции тела (пример: вращение детского волчка или юлы произвольной формы). Моменты инерции относительно главных осей называются главными моментами инерции.
Аналогично вышесказанному можно определить момент импульса относительноточки(вектор L ) иотносительнооси(проекциявектораLz):
→ |
→ → |
→ → |
, |
(4.19) |
||
L |
= r p |
= m r v |
||||
|
|
|
|
|
|
|
где pr = mνr – импульс (материальной) точки А, р. Важно отметить, что моментом импульса относительно точки может обладать и тело, движущееся поступательно (достаточно наличие импульса и плеча). Тело, обладающее импульсом, может не обладать моментом импульса относительно одних точек (в отсутствие плеча) и обладать относительно других.
Единицы измерения [М]=Н м (не путать с [А]=Дж=Н м), а
[L]= кг см2 .
→ |
→ |
p = mνr |
→ |
→ |
В общем случае F b/ b/ |
v (неколлинеарна) и |
, т.е. и M b/ b/ |
L , |
но если полюс (точка) О неподвижен, то импульс р точки А сонаправлен с ее скоростью νr = (rr)t' , тогда:
|
|
|
|
|
|
|
|
|
→ |
|
→ → |
|
|
|
→ → |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
M |
= |
r F |
= r |
dp |
, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
→ / |
|
→ → |
/ |
d → → |
|
|
|
|
|
|
→ |
|
|
|
|
|
→ |
|
→ |
|
||||
|
|
|
|
|
|
dr |
→ |
|
|
→ dp |
→ dp |
|
|||||||||||||
т.к. L |
|
= |
r p |
= |
|
r p |
= |
|
|
|
|
|
|
p |
|
|
+ r |
|
= r |
|
, |
||||
|
|
|
|
|
|
|
dt |
|
|
dt |
dt |
||||||||||||||
|
|
t |
|
|
|
t |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
→→ |
{ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→→ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
v p |
|
|
|
|
|
|
=0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
=m v v |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тоестьполучаютосновноеуравнениединамикивращательногодвижения:
→ |
|
|
|
dL |
→ |
|
|
= M . |
(4.20) |
||
dt |
|||
|
|
Этот закон остается справедливым и для системы материальных точек, в этом случае
41
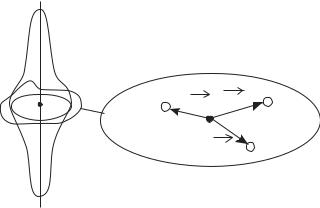
→→
=∑LiL
i
→ |
→ |
|
и M = ∑M i . |
(4.21) |
|
i
Особенность вращения ТТ, по сравнению с системой несвязанных друг с другом материальных точек, заключается в том, что при вращении ТТ вокруг неподвижной оси все его элементы движутся по окружностям, причем угловая скорость вращения ω для них одинакова (а линейная раз-
личная). Поэтому естественным будет выразить вектор L через скорость ω.
O/
C |
∆m1 r ri |
∆mi |
|
C r2 |
∆m2 |
O
Рис. 4.11.
Разобьем ТТ (рис. 4.11), вращающееся относительно оси ОО/, на элементы (материальные точки). Момент импульса каждого элемента
|
→ |
→ |
→ |
|
|
∆Li = ri |
∆mi vi . |
||
|
|
|
|
|
→ |
→ → |
(см. лекция 1, п.1) |
||
С учетом равенства v |
= r ω |
|||
|
|
|
|
|
|
→ |
|
|
|
→ |
→ |
→ → |
→ |
→ → |
∆Li = ri |
∆mi ω ri |
= ∆mi ri ω ri . |
||
|
|
|
|
|
Вматематикеизвестно, чтодвойноевекторноепроизведениеимеет вид
→ →→ = → →→ −→ → →a b c b a c c a b ,
→ → → |
|
→ |
→→ |
→ |
→ → |
= |
||
т.е. ri ωri |
|
=ω ri ri |
− ri |
ωri |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
14243 |
|
|||
→ →
=0, ω ri
→
ri2 ω.
Таким образом,
42
→ |
= (∆m r |
→ |
→ |
∆L |
2 )ω = ∆I |
ω , |
|
i |
i i |
i |
|
где ∆Ii – момент инерции i–го элемента.
Суммируя (интегрируя) по всем элементам, получают:
→ |
→ |
L |
= I ω . |
(4.22)
(4.23)
С учетом формул (4.20) и (4.23) получаем еще одну форму записи основного уравнения динамики вращательного движения:
→ |
→ |
|
|
|
→ (*) |
= I ε , |
|
dL |
= M = I dω |
(4.24) |
|
dt |
dt |
|
|
где ε – угловое ускорение.
Переход (*) в формуле (4.24) справедлив, если конфигурация системы (форма и размеры ТТ, положение оси) остается постоянной, тогда момент инерции I≠ƒ(t)=const.
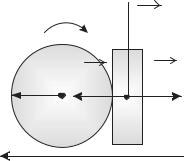
Пример. Вал массой m и радиусом R вращался с частотой n. К цилиндрической поверхности вала прижали тормозную колодку с силой F, под действием которой вал остановился, спустя время t. Определить коэффициент трения f.
Решение. Вал (сплошной цилиндр, см. рис. 4.12), участвуя во вращательном движении, останавливается под действием момента силы трения.
Ox: F–N=0 N=F, тогда Mтр=FтрR=ƒNR=ƒFR=Iε, согласно формуле
(4.24).
|
mR2 |
|
ω −ω0 |
|
|
|
mR2 |
|
|
|
0 |
− 2 π n |
|
|
|
|||
|
|
|
|
|
|
|
||||||||||||
Ответ: |
f = |
|
|
|
|
|
|
/(FR)= |
|
|
|
|
|
|
|
|
|
/(FR). |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
t |
|
|
2 |
|
|
|
|
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
 Fтр
Fтр
R |
F |
N |
|
O |
|
x
Рис. 4.12
При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы, так как внутренние силы взаимодей-
43

ствия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю). Согласно уравнению (4.21) для замкнутой системы имеем:
|
• |
|
→ |
→ |
|
|
→ |
|
dL |
= ∑Miвнешн = 0, |
|
|
L |
= |
(4.25) |
||
|
dt |
||||
|
|
|
i |
|
|
→ |
= const . |
|
|
|
|
т.е. L |
|
|
|
|
Значит, для замкнутых систем выполняется закон сохранения момента импульса.
Пример. В крайнюю от неподвижной оси вращения ОО/ точку А покоящейся системы жестко соединенных между собой тонких однородных одинаковых стержней, массой М и длиной l каждый (см. рис. 4.13), ударяется летящий со скоростью v мячик массой m и прилипает в точке А. Определить угловую скорость системы в начальный момент после удара. Трением при вращении системы пренебречь. Вектор скорости мяча считать направленным по нормали к плоскости конструкции из стержней.
Рис. 4.13
Решение. Так как рассматривается неупругий удар, то ударные или мгновенные силы в момент столкновения настолько велики, что действием внешних сил можно пренебречь и считать систему замкнутойr r . В такой системе выполняется закон сохране-
ния момента импульса (4.25): L1 = L2 . Хотя мяч сначала и движется поступательно, до
прилипания в точке А, он обладает моментом импульса относительно оси ОО/ L1=mνl. После столкновения для системы стержни – мяч:
L1 = L2 = Iω = (I1 + I2 + I3 + I мяча )ω .
Ответ: ω = mvlI , где I = 0 + Ml3 2 + Ml2 + ml2 .
Если работа силы идет только на вращение тела, т.е. на увеличение кинетической энергии (КЭ) вращения, то
44

dA = dT = Fds = Frdϕ = Mdϕ = Iεdϕ = I ddtω dϕ = Iωdω .
При увеличении скорости вращения от 0 до ω КЭ вращения равна
ω |
Iω2 |
|
|
|
Tвр = A = ∫Iωdω = |
|
. |
(4.26) |
|
2 |
||||
0 |
|
|
Пример. Сплошной цилиндр массой m и радиусом R скатывается без проскальзывания с наклонной плоскости высотой h. Определить скорость цилиндра у основания наклонной плоскости. Трением пренебречь.
Решение. Трением пренебрегают, т.е. в системе не будет неконсервативных сил. Для нее выполняется закон сохранения механической энергии. Так как цилиндр движется без проскальзывания, то угловая скорость его вращения вокруг своей оси симметрии и линейная скорость точек на ободе, равная по модулю скорости поступательного движения его центра масс, связаны соотношением ω=ν/R и, следовательно,
|
|
|
|
|
|
|
|
mR2 |
|
|
v |
|
|
|
|
|||
|
|
mv2 |
|
Iω2 |
|
mv2 |
|
|
|
|
|
|
3 |
|
|
|
||
mgh = |
|
|
|
2 |
|
R |
mv |
2 |
|
|||||||||
|
+ |
|
= |
|
+ |
|
|
|
|
|
= |
|
|
. |
||||
2 |
2 |
2 |
|
2 |
|
|
4 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: v = |
2 3gh . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3. Гироскоп
Гироскоп (Г) – с греческого языка можно перевести словами: круг, кружусь, вращаюсь и смотрю, наблюдаю. В широком смысле под гироскопом понимают обладающее большим моментом инерции быстро вращающееся ТТ, ось вращения которого может изменять свое положение в пространстве. Простейший пример гироскопа – детский волчок или юла, у которых нижний конец оси не закреплен, поэтому она может изменять свое положение в пространстве. Если гироскоп обладает симметрией и ось вращения проходит через центр инерции (масс) С тела, то он называется астатическим (уравновешенным), в противном случае – тяжелым.
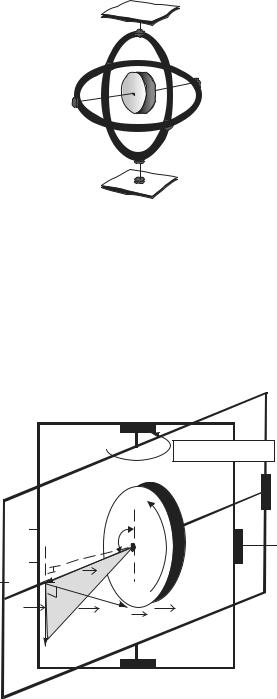
В технике, в основном, применяют уравновешенные Г, у которых
свободный поворот оси Г обеспечивают, закрепляя его, например, в рам-
ках (кольцах) карданова подвеса (рис. 4.14, 4.15), позволяющего оси за-
нять любое положение в пространстве.
Гироскоп характеризуется двумя свойствами:
1) ось Г стремится сохранить в пространстве приданное ей направление;
45
2) если на ось начинает действовать сила (пара сил), то Г будет отклоняться в направлении, перпендикулярном плоскости действия силы
(сил).
Это происходит потому, что момент сил всегда направлен перпендикулярно плоскости, в которой лежат сила и ее плечо. В результате Г начинает вращаться с постоянной угловой скоростью в направлении действия моментов сил.
Рис. 4.14
Это движение называют прецессией, а проявление второго свойства Г в целом – гироскопическим эффектом. На указанных особенно-
стях Г основано его применение в технике для навигации, проведения маркшейдерских, топографических, геодезических и др. работ.
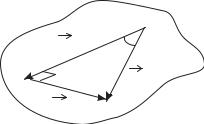
При приложении силы F (рис. 4.15), вследствие возникновения ее момента, Г будет поворачиваться относительно оси АА/, а не DD/.
A
D
 O
O 
 F
F
Прецессия |
|
|
O/ |
l α C |
D/ |
r |
|
M=[ r F ] |
|
A/
Рис. 4.15
46
Так как момент импульса Г будет меняться, то из прямоугольного треугольника (рис.4.16)
dL = Ltg(dβ)≈ Ldβ , dβ = |
dL (4.25) |
Mdt |
|
|
L |
= |
L |
. |
|
|
|
|
||
C |
|
|
|
|
L dβ |
|
|
|
|
L/ |
|
|
|
|
dL |
|
|
|
|
Рис. 4.16
Тогда угловая скорость прецессии
случае
ωp = |
dβ |
= |
M |
|
|
|
или в общем |
||
dt |
L |
|||
|
|
|
|
→ |
|
→ |
→ |
, |
(4.27) |
||
|
|
|
|
M = ω |
p |
L |
|||||
|
|
|
M |
|
|
|
|
|
|
||
т.е. ω |
p |
= |
, где ω – угловая скорость собственного вращения Г, |
||||||||
Iωsinα |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
вокруг оси ОО/.
4.4. Законы сохранения и симметрия пространства-времени
Как уже говорилось при любом (поступательном и/или вращательном)
движенииТТ(системыматериальныхточек) необходимоучитыватьтолько внешниесилы, таккаквнутренниесилывзаимодействиядвухлюбыхэлементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой – их векторная (геометрическая) сумма равна нулю и векторная суммаихмоментовтакжеравнанулюпоIII законуНьютона. Однакоэтивыводы можносделатьисходяизII законаНьютона(основнойзакондинамики) исвойств симметриипространства– однородностииизотропности.
Ранее (лекции 2, 3, 4) говорилось о том, что законы сохранения импульса (момента импульса) и энергии являются следствием однородности пространства и времени соответственно. Однородность пространства за-
ключается в том, что при параллельном переносе физической системы
на любое расстояние ее физические свойства и законы движения не
47
меняются, а изотропность пространства в том, что эти свойства и законы не меняются при повороте системы как целое на любой угол.
Иначе говоря, физические законы не изменятся, если систему как целое без изменения внутреннего строения передвинуть в пространстве путем параллельного переноса на величину dr (повернуть как целое на угол dϕ ). В частности, при этом должна быть равна нулю работа всех (внутренних) сил в системе, тогда получают:
- для поступательного движения (вспомним III закон Ньютона)
|
|
→ → |
→ |
→ |
→ |
→ |
|
δ A = ∑ ∑Fnk dr |
= ∑∑Fnk dr |
= 0 т..к.dr |
≠ 0, то∑∑Fnk |
= 0; |
|||
n k |
|
n k |
|
|
n k |
|
|
- для вращательного движения |
|
|
|
||||
|
→ |
→ |
→ |
→ |
→ |
→ |
|
δ A = ∑ |
∑M nk dϕ |
= ∑∑M nk dϕ = 0 т..к.dϕ ≠ 0, то∑∑M nk = 0 . |
|||||
n k |
|
n k |
|
|
n k |
|
|
Однородность времени заключается в том, что физические законы инвариантны относительно выбора начала отсчета времени, т.е. в
одинаковых условиях все процессы в замкнутой системе будут протекать одинаково в разные моменты времени. В частности, при неизменности внутреннего строения потенциальная энергия (ПЭ) U≠ƒ(t), то есть ∂U/dt=0. Тогда при отсутствии в системе непотенциальных сил или отсутствии совершения ими работы из уравнения (3.10) лекции 3 в любой момент времени вытекает закон сохранения механической энергии.
Следует заметить, что уравнения классической механики инвариантны по отношению к направлению хода времени – его возраста-
нию или убыванию. Из сохранения вида уравнений механики при замене переменной t на –t следует принципиальная возможность обратимости механических процессов: если механическая система совершает под действием сил какое-либо движение, то она под действием этих же сил может совершать и прямо противоположное движение, при котором система будет проходить через те же самые состояния в обратном порядке. В общем
случае обратимости для процессов иной (немеханической) природы может и не существовать.
48
ЛЕКЦИЯ 5. ТЯГОТЕНИЕ. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
1.Законы И.Кеплера и закон всемирного тяготения И.Ньютона. Поле тяготения как пример центрального поля, его напряженность и потенциал.
2.Космические скорости (первая – четвертая).
3.Неинерциальные системы отсчета. Силы инерции. Вес тела и невесомость.
5.1. Законы И.Кеплера и закон всемирного тяготения И.Ньютона. Поле тяготения как пример центрального поля, его напряженность и потенциал
Издревле человек пытался ответить на вопросы: кто он, для чего он, как устроен он и окружающий его мир? Эти вопросы остаются актуальными и по сегодняшний день, хотя человек приобрел довольно много знаний об устройстве Вселенной. Процесс познания не всегда протекал спокой-
но и эволюционно. Например, смена господствовавшей более 1350 лет гео-
центрической или птолемеевой (К. Птолемей (II в. н.э.)) системы мира
(Земля – центр Вселенной, всё вращается вокруг нее) на гелиоцентрическую (современную: Солнце – одна из звезд, а планеты, в т.ч. и Земля, вра-
щаются вокруг него) систему мира Н. Коперника (1473–1543) противоре-
чила интересам католической церкви (ее догматам). Н.Коперник под страхом пыток и смертной казни публично отрекся от своей системы. Труд Н.Коперника «Об обращении небесных сфер» был под запретом Папы Римского вплоть до 1835г. Тем не менее истина нашла себе дорогу, и уже к XVII веку гелиоцентрическая система мира была признана большинством ученых.
В начале XVII века И. Кеплер (1571–1630) на основе собственных наблюдений и 35-летних наблюдений Т.Браге (1546–1601) сформулиро-
вал три закона движения планет:
I. Современная формулировка: при невозмущенном движении (задача двух тел) орбита движущейся материальной точки (небесного тела, в т.ч. и планеты) есть кривая второго порядка, в одном из фокусов которой находится Солнце, т.е. орбита материальной точки при невозмущенном движении – одно из конических сечений (окружность, эллипс (для планет), парабола, гипербола). Формулировка И. Кеплера (1609г., труд «Новая астрономия»): каждая планета движется по эллипсу в одном из фокусов которого находится Солнце.
II. Современная формулировка: при невозмущенном движении площадь, описываемая радиусом-вектором движущейся точки, изменяется пропорционально времени (закон площадей). Формулировка И. Кеплера
49
(II и III законы опубликованы в 1619г., труд «Гармония мира»): радиусвектор планеты за равные промежутки времени описывает равные площади.
III. Современная формулировка: при невозмущенном эллиптическом движении двух материальных точек (планет) вокруг центрального тела (Солнца (m0)) произведения квадратов времен обращения на суммы масс центральной и движущейся точек относятся как кубы больших полу-
осей их орбит (III закон относится уже не к одной планете, а к Солнечной системе, рис.5.1):
Т2 |
|
m + m |
|
a3 |
|
|||
|
1 |
|
0 |
1 |
= |
1 |
, |
|
Т2 |
m + m |
a3 |
||||||
|
|
|
||||||
2 |
|
0 |
2 |
|
2 |
|
||
при m0>>mi:
Т12 = a13 Т22 a23 .
Формулировка И. Кеплера: квадраты времен обращения планет относятся как кубы больших полуосей их эллиптических орбит:
|
Т2 |
= |
r3 |
|
|
1 |
1 . |
(5.1) |
|
|
Т2 |
|
r3 |
|
|
2 |
|
2 |
|
|
r |
b |
a |
|
A |
|
|
П |
|
O |
|
F2 |
||
|
|
|
||
|
r F1 |
b |
|
|
|
|
|
|
Рис. 5.1
Из формулы (5.1) следует, что отношение |
r3 |
= const = K – кон- |
|
T 2 |
|||
|
|
станта Кеплера.
В первом приближении орбиты планет принимают за круговые с
учетом:
|
|
|
v2 |
|
2 |
|
2π |
2 |
r3 |
|
4π 2 K |
, |
|
a |
n |
= |
|
=ω |
|
r = |
|
|
|
|
= |
|
|
r |
|
|
r 2 |
r 2 |
|||||||||
|
|
|
|
|
T |
|
|
|
|||||
тогда сила, действующая на планету, равна:
50
