lection_part1-2

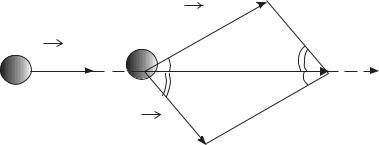
ν1/

Рис. 3.8

Абсолютно неупругий удар (АНУ). В этом случае тела объединяют-

ся и двигаются как одно целое. Потеря механической энергии при неупругом ударе происходит потому, что в этом случае помимо сил, пропорциональных деформациям, действуют силы, пропорциональные скорости – подобные силам сопротивления. При АНУ выполняется закон сохранения импульса и рассеивается часть КЭ ∆T:

Рассмотрим частный случай АНУ: молот(ок) m1 забивает сваю (гвоздь) m2, т.е. ν2=0, тогда

Чем больше величина m1 по сравнению с m2, тем больше КЭ ∆T и, следовательно, КПД – η.

31

жень, кольцо, диск), параллелепипед, шар и т.д.), для тел неправильной формы интегралы находятся численно.

Вычисление моментов инерции во многих случаях можно упростить, используя соображения подобия и симметрии, а также теорему Гюйгенса-Штейнера (Х.Гюйгенс (1629–1699), Я. Штейнер (1796–1863)) и ряд некоторых соотношений.

dm

r

r/

O a A

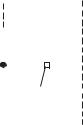
Рис. 4.1

Найдем связь между моментами инерции тела относительно двух неподвижных параллельных осей. Пусть оси перпендикулярны плоскости рисунка и проходят соответственно через точки О и А (все точки находятся в плоскости рис. 4.1). Используя теорему косинусов для данного треугольника, получают:

Последнее слагаемое можно представить в виде ∫r dm = m RC , где

RC – составляющая радиуса-вектора центра масс С тела относительно оси О, параллельная плоскости рисунка. Здесь следует вспомнить, что

альных точек (см. лекцию 2, п. 2.3), а в случае непрерывного распределе-

ли же ось О проходит через центр масс тела, то третье слагаемое в правой части равно нулю и получают уравнение, которое выражает теорему Гюйгенса-Штейнера: момент инерции тела относительно какой-либо

33

оси равен моменту инерции его относительно параллельной оси, проходящей через его центр масс С, сложенному с величиной ma2, где а – расстояние между осями, m – масса тела.:

Далее вычисляют моменты инерции некоторых тел правильной фор-

мы.

1. Тонкий однородный стержень (длина l, масса m, линейная плотность τ=m/l=const):

а) ось вращения ОО/ проходит перпендикулярно стержню через его центр масс С (рис. 4.2).

O/ A/

Рис. 4.2

В силу симметрии получают:

б) ось вращения АА/ проходит перпендикулярно стержню через его конец. По теореме Гюйгенса-Штейнера (4.4) получают:

2. Однородные прямоугольная пластина и параллелепипед (ли-

нейные размеры a, b, c, масса m). Согласно теореме Пифагора и формулы (4.1) для точки m (рис. 4.3) имеют:

I x = m( y2 + z2 ) , I y = m(x2 + z2 ) , I z = m(x2 + y2 ) ,

тогда их сумма равна:

I x + I y + I z = 2m(x2 + y2 + z2 ) = 2mR2 .

34

X

Рис. 4.3

Можно увидеть, что если рассматривать любые три взаимно перпендикулярные оси, пересекающиеся в точке О, то моменты инерции Ix, Iy, Iz будут меняться, а их сумма останется постоянной. Обозначив в случае дискретного

распределения масс (система материальных точек) Φ = ∑mi Ri2 или для не-

i

прерывного распределения масс (в твердом теле) Φ = ∫R2dm , можно записать, что

На основании вышеизложенного имеем:

а) если дана тонкая прямоугольная пластина, то можно считать, что вещество распределено тонким слоем по плоскости XOY, т.е. z-координаты всех точек ≈0. Тогда формула (4.7) примет вид

следовательно

I x + I y = I z .

Y

Рис. 4.4

35

Так как дана тонкая однородная прямоугольная пластина, то представляют, что все вещество смещено (направление смещения обозначено стрелками на рис. 4.4) параллельно оси ОХ и сконцентрировано на оси ОY. При этом расстояния всех материальных точек до оси ОХ не изменятся. В результате получают тонкий однородный стержень массы m и длины b (случай 1, а), а с учетом формул (4.5) и (4.8):

На рис. 4.4 ось OZ проходит через точку С и плоскости XOY – плоскости рисунка;

б) формула (4.9) справедлива и для однородного прямоугольного па-

раллелепипеда. В этом можно убедиться, если мысленно сжать параллелепипед вдоль одной из его геометрических осей в тонкую пластинку. При

этом масса его и расстояния всех точек до этой оси не изменятся.

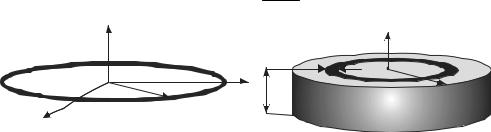
3. Однородное тонкое круглое кольцо (масса m, радиус R,). В силу

4. Однородный диск или сплошной цилиндр (масса m, радиус R,

объемом V). Начало координат (пересечение) трех взаимно перпендикулярных осей располагают в центре масс цилиндра (можно аналогично случаю 2, а) сместить все вещество вдоль оси ОZ, т.е. получить тонкий диск малой толщины h/, плотности ρ=m/V′, V′=π R2 h′ – объем после смещения, см. рис. 4.6), для которого

36

Z

R

C Y

X

Рис. 4.7

5. Полый шар с бесконечно тонкими однородными стенками

(сфера массы m, радиуса R). Расположим начало координат (пересечение) трех взаимно перпендикулярных осей в центре сферы, в ее центре масс С (рис. 4.7), тогда в силу симметрии и формулы (4.7):

6. Сплошной однородный шар (масса m, радиус R, объем V). Рас-

положим начало координат (пересечение) трех взаимно перпендикулярных осей в центре шара и рассмотрим шар как совокупность тонких сфер. Момент инерции такого тонкого сферического слоя по формуле (4.14) будет

тогда момент инерции шара:

37

В некоторых задачах используется понятие момента инерции относительно точки. Поскольку ориентация различных элементов тела (ТТ) относительно его произвольной точки должна задаваться тремя координатами, то его инертность должна характеризоваться набором 9 чисел – тензором инерции (в математике используются скаляры – одно число, векторы – тройки чисел и тензоры – запись их представляет собой матрицу III порядка).

4.2. Момент силы и момент импульса относительно неподвижного начала.

Основной закон динамики вращательного движения. Закон изменения момента импульса. Кинетическая энергия

вращения (см. также лекцию 1, п.1)

Вращение является составляющей большинства рассматривае-

мых в механике движений. Каждый день мы являемся свидетелями великого космического вращения. Данные последних теоретических исследований говорят, что всё вокруг и мы сами по свойствам напоминаем вращающиеся с большой частотой поля.

Динамические характеристики – момент силы и момент импуль-

са, используемые при описании вращательного движения, играют в тео-

рии вращательного движения такую же большую роль, какую сила и импульс играют в динамике поступательного движения.

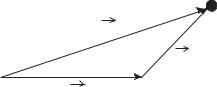
Рис. 4.8

Известно, что передвинуть массивный предмет (например, ящик) вручную тяжело, гораздо легче передвинуть его с помощью длинной палки, трубы (лома), т.е. перекантовать с помощью рычага, причем, чем длинней этот рычаг, тем легче это сделать (прикладывается меньшая сила при большей длине рычага (см. рис. 4.8)). Вспомним знаменитое изречение

Архимеда (ок. 286–212 гг. до н.э.): «Дайте мне точку опоры (и рычаг) и я переверну Землю».

38

Другой пример – взвешивание предметов на весах (см. рис. 4.9): при равных плечах (силы) весов li перевесит тот груз, масса которого mi больше, а если массы грузов равны, то перевесит груз, для которого плечо силы

li больше.

l1 l2

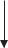m1g m2g

Рис. 4.9

Следует различать момент силы и момент импульса относительно точки и относительно оси, в первом случае – это вектора, а во втором – проекции векторов (скаляры).

Рис. 4.10

Пусть дана точка О (полюс), относительно которой находится мо-

мент силы. Моментом силы F относительно точки О называется векторное произведение (вектор) радиуса-вектора r , проведенного из точки О в точку А приложения силы на векторF :

При этом вектор M не изменится, если точку приложения силы F перенести в любую другую точку, расположенную на линии действия силы,

39

например в точку А/. При этом параллелограмм ОАВС перейдет в параллелограмм ОА/В/С. Оба параллелограмма имеют одинаковые основание и высоту,

аследовательно, и площадь.

Вотличие от полярных векторов νr, аr, рr, F (именно их изучают в

школе), вектора, характеризующие вращательное движение

→ → → → →

d ϕ,ω, ε , M , L , не имеют конкретной точки приложения (см. также лекция 1, п.1), их называют скользящими. Так, вектор M можно откладывать от любой точки параллельно одному из направлений, полученному в резуль-

тате векторного произведения (по свойствам векторного произведения r

M перпендикулярно плоскости, в которой лежат два перемножаемых век-

→ → → →

тора – M r , M F ), направление вектора M совпадает с направлением

поступательного движения правого винта при его вращении от вектора r к

Fr (в математике термин – «левая тройка»). r

Главным моментом M нескольких внешних сил, действующих на систему, относительно точки О называется сумма моментов их относи-

тельно этой точки (принцип независимости действия сил):

где силы Fri считают приложенными к одной точке О, что можно получить путем параллельного переноса векторов Fi (часто в механике для удобства при решении задач силы рассматривают как приложенные к центру масс тела, хотя это не для всех сил так, пример – сила трения Fтр приложена к

поверхности тела).

При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы, так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю).

Моментом силы относительно некоторой оси OZ (рис. 4.10) называется скаляр – проекция вектора M на эту ось (Mz).

Ось, положение которой в пространстве остается неизменным при вращении вокруг нее тела в отсутствии внешних сил, называется свобод-

ной осью тела. Можно показать, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендику-

40