1. Комплексные числа. Комплексным числом называется упорядоченная пара вещественных чисел X и Y , первое из которых X называется действительной частью, а второе Y – мнимой частью этого ,пользоваться декартовой прямоугольной системой координат. При этом комплексное число Z=(X,Y) изображается или точкой М с координатами (X,Y), или вектором ОМ, идущим из начала координат в точку М. Если ввести полярную систему координат так, чтобы полюс находился в начале О декартовой системы координат, а полярная ось была направлена вдоль положительного направления оси Ох то декартовы координаты (Х,Y) и полярные координаты (ρ,θ) любой точки М, как известно, связаны формулами:
ρ = (x2+y2)½
x=ρ
,
y=ρ
θ=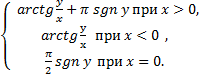
Эти формулы приводят нас к тригонометрической форме записи комплексного числа z=(x,y):
Z=(x,y)=x+iy=(ρ
=ρ(cosθ+isinθ)
В тригонометрической форме представления
число ρ называют модулем, а угол θ
аргументом комплексного числа.
Алгебраическая запись комплексного числа:
Z=a + ib ( i2=(-1)) где а это действительная часть комплексного числа , а ib это мнимая часть комплексного числа.
Показательная запись комплексного числа имеет вид:
Z=|Z|eiθ , где |Z|= ρ = (x2+y2)½
____________________________________________________________________________________________
2.Арифметические операции над комплексными числами:
Суммой двух комплексных чисел Z1=(X1,Y1) и Z2=(X2,Y2) называется комплексное число Z вида: Z=(X1+X2, Y1+Y2).
Произведением двух комплексных чисел Z1=(X1,Y1) и Z2=(X2,Y2) называется комплексное число Z вида: Z=(X1 X2-Y1 Y2, X1 Y2+X2 Y1).
Свойства суммы и произведения двух комплексных чисел:
Z1+Z2=Z2+Z1 (переместительно свойство суммы)
(Z1+Z2)+Z3=Z1+(Z2+Z3) (сочетательное свойство суммы)
Z+(0,0)=Z (особая роль числа (0,0)
Для каждого числа Z=(x,y) существует противоположное ему число Z’=(-x,-y) такое что Z+Z’=(0,0)
Z1 Z2= Z2 Z1 (переместительное свойство произведения)
(Z1 Z2) Z3=Z1( Z2 Z3) (сочетательное свойство произведения)
Z∙(1,0)=Z (особая роль числа (1,0))
Для любого комплексного числа Z=(x,y),не равного нулю , существует обратное ему число 1/Z=(x/x2+y2, -y/x2+y2) такое ,что Z∙1/Z=(1,0) (Z1+Z2)∙Z3=Z1∙Z3+Z2∙Z3 (распределительное свойство произведения относительно суммы)
Исходя из свойств можно определить разность и частное двух комплексных чисел:
Разностью двух комплексных чисел Z1=(X1,Y1) и Z2=(X2,Y2) называется такое комплексное число Z, которое в сумме с Z2 дает Z1. Z=(X1-X2, Y1-Y2)
Частным двух комплексных чисел Z1=(X1,Y1) и Z2=(X2,Y2) называется такое комплексное число Z, которое при умножении на Z2 дает Z1. Z=(x1x2+y1y2/x22+y22, x2y1-x1y2/x22+y22).
Возведение в степень
Z=a=ib=|z|
где θ=arg(z)
=
=
(cos(nθ)+sin(nθ))
– формула Муавра.
Корень n-ной степени из комплексного числа z называется такое комплексное число W, что
=Z
; |Z|=
;
Z=a+ib;
Z=|Z|
;
=
=
;
Корни n степени из Z
расположены в вершинах правильного
n-угольника вписанного в
окружность радиуса
c центром в точке О(0,0).
3. Бином Ньютона. Метод математической индукции
Бином Ньютона – это формула, выражающая выражение (a + b)n в виде многочлена. формула имеет вид:
n
(a+b)n =a n+C1n a n -1 b+C 2na n -2 b 2+…+b n = ∑C ina n -i b i
i=0
Пример. В разложении (x k +y p ) n найти члены, содержащие хa, eсли k=3, p=2, n=8, a=9
По формуле Бинома Ньютона имеем: (x k +y y ) n = ∑C in(x k ) n -i (yp) i
С учетом числовых значений: (x 3 +y 2 ) 8 = ∑C i8* x 3(8 –i) *y2 i
Найдем число i, соответствующее данному члену: 3(8-i)=9, i=5
Находим: C 58*x 9 * y10 =8!/( 5!*3!)*x 9 *y10=56x 9 *y10
Метод математической индукции: чтобы доказать что некоторая теорема верна для всякого натурального числа n достаточно доказать: 1) что эта теорема справедлива для n=1 2) что елси эта теорема справедлива для числа n то она справедлива также и для следующего натурального числа n+1
Пример: Доказать, что для любого натурального числа n справедливо неравенство; 1+2+…+n = n (n+1)/2
Решение: 1) для n=1: 1=1(1+1) 2=2 2) Если неравенство выполняется для числа n то должно выполняться для n+1:
n=n+1; 1+2+…+n+(n+1)=(n+1)(n+2)/2; (n(n+1)/2)+(n+1)=(n+1)(n+1)/2; (n/2)+1=(n/2)+1; равенство доказано.
____________________________________________________________________________________________