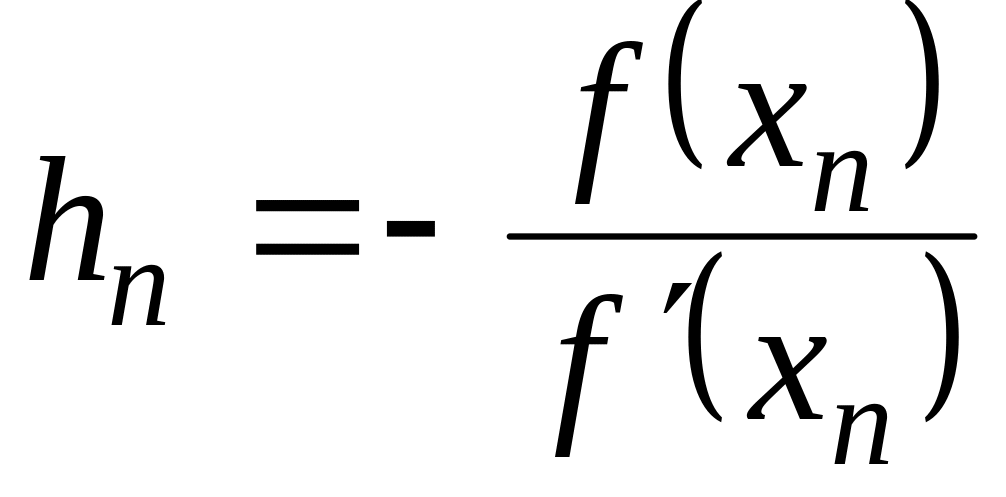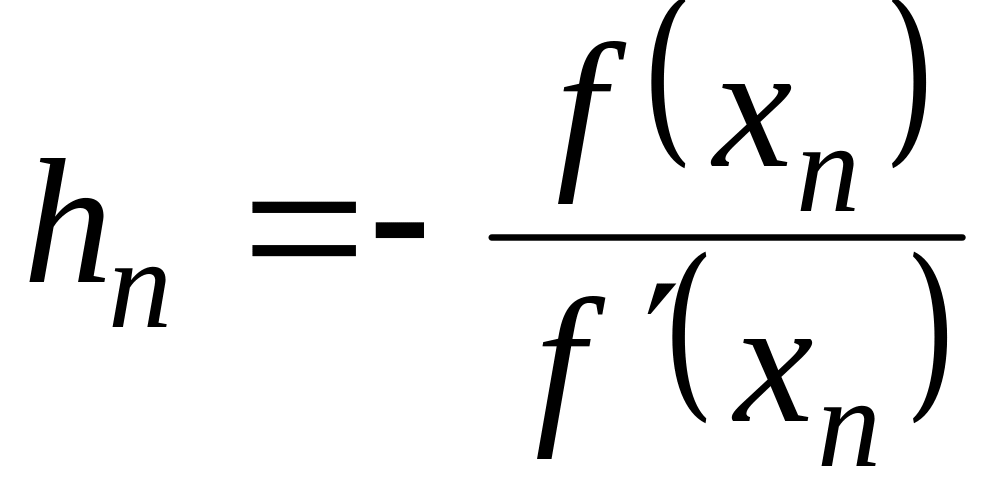- •1 Основні поняття теорії похибок
- •1.1 Поняття похибки
- •1.2 Дії над наближеними числами
- •1.3 Пряма та обернена задачі теорії похибок
- •1.3 Джерела похибок обчислень
- •2 Обчислення значень функцій
- •2.1 Обчислення значень полінома. Схема Горнера
- •2.2 Наближене знаходження сум числових рядів
- •2.3 Обчислення значень аналітичної функції
- •2.4 Обчислення значень показової функції
- •2.5 Обчислення значень логарифмічної функції
- •2.6 Обчислення значень тригонометричних функцій
- •3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •3.1 Концепція методів
- •3.2 Метод простої ітерації
- •3.3 Метод Гаусса-Зейделя
- •4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь
- •1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.
- •2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .
- •4.1 Відділення коренів
- •4.2 Метод половинного поділу (метод дихотомії)
- •4.3 Метод хорд (спосіб пропорційних частин)
- •4.4 Метод Ньютона (метод дотичних)
- •4.5 Комбінований метод
- •4.6 Метод ітерації
- •4.7 Метод ітерації для системи двох рівнянь
- •5 Обробка емпіричних даних
- •5.1 Інтерполяція та екстраполяція
- •5.2 Концепція інтерполяції та екстраполяції
- •5.3 Лінійна і квадратична локальні інтерполяції
- •5.4 Глобальна інтерполяція. Многочлен Лагранжа
- •5.5 Глобальна інтерполяція. Многочлен Ньютона
- •5.6 Апроксимація
- •При цьому вимагається, щоб
- •Побудуємо емпіричний точковий графік.
- •Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
- •6 Наближене обчислення визначених інтегралів
- •6.1 Концепція чисельного інтегрування
- •6.2 Методи прямокутників та трапецій
- •6.3 Метод Симпсона
- •6.4 Метод Монте-Карло
4.4 Метод Ньютона (метод дотичних)
Нехай корінь рівняння
(4.12)
Відділений
на відрізку
,
причому
та
неперервні та зберігають сталі знаки
при
.
Знайшовши яке-небудь
-е
наближене значення кореня
![]() ,
ми можемо уточнити його методом Ньютона
по формулі:
,
ми можемо уточнити його методом Ньютона
по формулі:
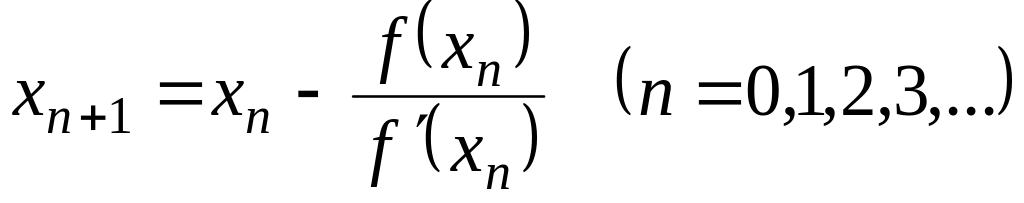 .
(4.13)
.
(4.13)
Геометрично метод Ньютона еквівалентний заміні невеликої дуги кривої дотичною, проведеною в деякій точці кривої. Справді, покладемо для визначеності, що при та (рис. 4.5).
Виберемо,
наприклад,
![]() ,
для якого
,
для якого
![]() .
Проведемо дотичну до кривої
в точці
.
Проведемо дотичну до кривої
в точці
![]() .
.
Для
першого наближення кореня
візьмемо абсцису точки перетину цієї
дотичної з віссю
![]() .
Через точку
.
Через точку
![]() знову проведемо дотичну, абсциса точки
перетину якої з віссю
дасть нам друге наближення
кореня і т. д. (рис. 4.5).
знову проведемо дотичну, абсциса точки
перетину якої з віссю
дасть нам друге наближення
кореня і т. д. (рис. 4.5).
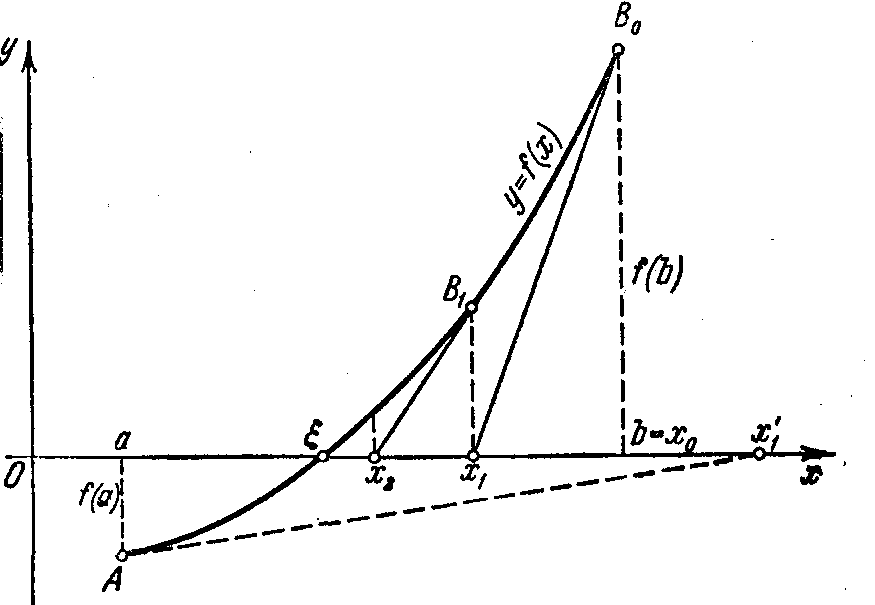
Рис. 4.5
Очевидно,
що рівняння дотичної в точці
![]() є
є
![]() .
.
Поклавши
![]() ,
отримаємо формулу (4.13):
,
отримаємо формулу (4.13):
.
Зауважимо,
що, якщо у нашому випадку покласти
![]() і, отже,
і, отже,
![]() ,
то, провівши дотичну до кривої
в точці
,
ми отримали б точку
,
то, провівши дотичну до кривої
в точці
,
ми отримали б точку
![]() (рис. 4.5), що лежить поза відрізком
,
тобто при такому виборі початкового
значення метод Ньютона не приведе
до мети. Таким чином, у даному випадку
«хорошим» початковим наближенням
(рис. 4.5), що лежить поза відрізком
,
тобто при такому виборі початкового
значення метод Ньютона не приведе
до мети. Таким чином, у даному випадку
«хорошим» початковим наближенням
![]() є таке, для якого виконується нерівність
є таке, для якого виконується нерівність
![]() (4.14).
(4.14).
Це правило є загальним для методу Ньютона.
Зауваження
1. Якщо: 1) функція
визначена і неперервна при
;
2)
![]() ;
3)
;
3)
![]() при
;
4)
існує всюди і зберігає сталий знак, то
при застосуванні методу Ньютона для
знаходження кореня рівняння
,
який лежить у інтервалі
при
;
4)
існує всюди і зберігає сталий знак, то
при застосуванні методу Ньютона для
знаходження кореня рівняння
,
який лежить у інтервалі
![]() ,
за початкове наближення
,
за початкове наближення
![]() можна прийняти будь-яке значення
можна прийняти будь-яке значення
![]() .
Зокрема, можна покласти
.
Зокрема, можна покласти
![]() або
або
![]() .
.
Зауваження
2. З формули (4.13) видно, що чим більше
числове значення похідної
у околі даного кореня, тим менша поправка,
яку треба додати до
-го
наближення, щоб отримати
![]() -е
наближення. Тому метод Ньютона особливо
зручно застосовувати тоді, коли у околі
даного кореня графік функції має велику
крутизну. Якщо ж чисельне значення
похідної
біля кореня мале, то поправки будуть
великими, і обчислення кореня за методом
Ньютона може виявитися дуже довгим, або
і взагалі неможливим. Отже, якщо крива
біля точки перетину з віссю
майже горизонтальна, то застосовувати
метод Ньютона для розв’язування рівняння
не рекомендується.
-е
наближення. Тому метод Ньютона особливо
зручно застосовувати тоді, коли у околі
даного кореня графік функції має велику
крутизну. Якщо ж чисельне значення
похідної
біля кореня мале, то поправки будуть
великими, і обчислення кореня за методом
Ньютона може виявитися дуже довгим, або
і взагалі неможливим. Отже, якщо крива
біля точки перетину з віссю
майже горизонтальна, то застосовувати
метод Ньютона для розв’язування рівняння
не рекомендується.
Для оцінки похибки -гo наближення знову можна скористатися формулою
![]() (4.15),
(4.15),
де
![]() — найменше значення
— найменше значення
![]() на відрізку
.
на відрізку
.
Має місце ще одна формула для оцінки точності наближення :
![]() (4.16).
(4.16).
Отже, якщо задатися якоюсь точністю , то обчислення за методом Ньютона можна виконувати до тих пір, коли різниця між двома сусідніми наближеннями за абсолютною величиною стане меншою від . А потім прийняти значення кореня рівняння рівним останньому наближенню.
Приклад
1. Обчислити методом Ньютона від’ємний
корінь рівняння
![]() з п’ятьма вірними знаками.
з п’ятьма вірними знаками.
Розв’язок.
Послідовно
приймаючи у лівій частині рівняння
![]() ,
отримаємо
,
отримаємо
![]() .
.
Отже,
шуканий корінь
знаходиться в інтервалі
![]() .
Звузимо знайдений інтервал. Так як
.
Звузимо знайдений інтервал. Так як
![]() ,
то
,
то
![]() .
.
Перша та друга похідні:
![]()
У
останньому знайденому інтервалі похідні
зберігають сталі знаки:
та
.
Так як
![]() і
і
![]() ,
то можемо прийняти за початкове
наближення
,
то можемо прийняти за початкове
наближення
![]() .
Послідовні наближення
.
Послідовні наближення
![]() обчислюємо за такою схемою:
обчислюємо за такою схемою:
|
|
|
|
|
0 |
-11 |
3453 |
-5183 |
0,7 |
1 |
-10,3 |
134,3 |
-4234 |
0,03 |
2 |
-10,27 |
37,8 |
-4196 |
0,009 |
3 |
-10,261 |
0,15 |
-4185 |
0,00004 |
Так
як поправка
![]() є фактично різницею між двома сусідніми
наближеннями кореня, то можна покласти
є фактично різницею між двома сусідніми
наближеннями кореня, то можна покласти
![]() .
.
Приклад
2. Знайти за методом Ньютона найменший
додатний корінь рівняння
![]() з точністю
з точністю
![]() .
.
Розв’язок.
Побудувавши графіки функцій
![]() та
та
![]() (рис. 4.6), робимо висновок, що шуканий
корінь
знаходиться в інтервалі
(рис. 4.6), робимо висновок, що шуканий
корінь
знаходиться в інтервалі
![]() .
Перепишемо рівняння у вигляді
.
Перепишемо рівняння у вигляді![]() ,
матимемо:
,
матимемо:
![]()
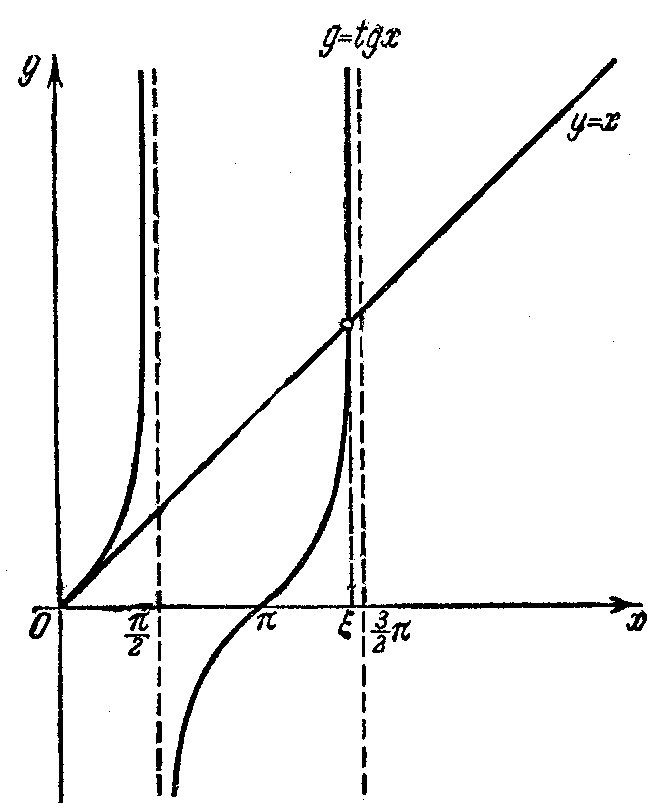
Рис. 4.6
Звідси
та
при
.
Так як
![]() ,
то за початкове наближення можна
прийняти
,
то за початкове наближення можна
прийняти
![]() .
Обчислення виконуємо за наступною
схемою:
.
Обчислення виконуємо за наступною
схемою:
|
|
|
|
|
0 |
|
-1 |
-4,712 |
|
1 |
|
-0,0291 |
-4,399 |
|
2 |
|
-0,00003 |
----- |
|
Надаємо можливість читачу самостійно здійснити оцінку похибки наближеного значення .