1.3 Пряма та обернена задачі теорії похибок

Пряма задача теорії похибок полягає в наступному: відомі похибки деякої системи величин, вимагається визначити похибку даної функції від цих величин.

Нехай задана диференційовна функція

і нехай – абсолютні похибки аргументів функції. Тоді абсолютна похибка функції

Звичайно на практиці — малі величини, добутками, квадратами і вищими степенями яких можна нехтувати. Тому можна покласти:

Отже

(1.2)

Звідси, позначаючи через граничні абсолютні похибки аргументів , і через – граничну похибку функції , для малих отримаємо:

(1.3)

Розділивши обидві частини нерівності (1.2) на , матимемо оцінку для відносної похибки функції .

(1.4)

Отже, за граничну відносну похибку функції можна прийняти:

(1.5)

Приклад 1. Знайти граничні абсолютну і відносну похибку об'єму кулі , якщо діаметр d = 3,7см ±0,05см, а .

Розв’язок. Розглядаючи і d як змінні величини, обчислюємо частинні похідні

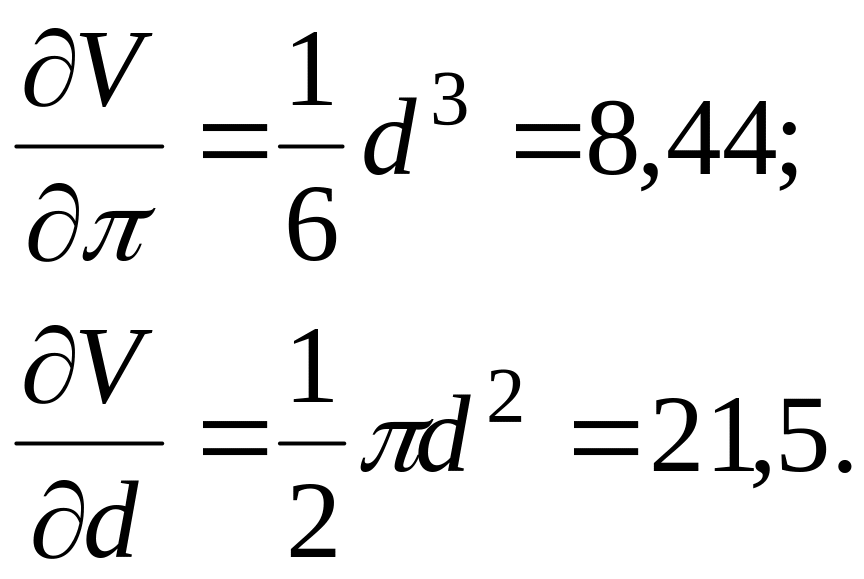
Через формулу (1.3) гранична абсолютна похибка об'єму

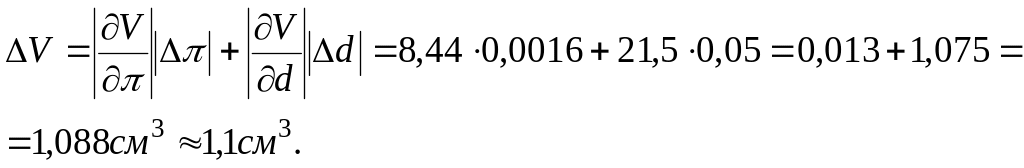
Тому

Звідси гранична відносна похибка об'єму

На практиці важлива також обернена задача теорії похибок: які повинні бути абсолютні похибки аргументів функції, щоб абсолютна похибка функції не перевищувала заданої величини.

Ця задача математично невизначена, оскільки задану граничну похибку функції можна забезпечити, встановлюючи по-різному граничні абсолютні похибки її аргументів.

Найпростіше рішення оберненої задачі дається так званим принципом рівних впливів. Згідно цьому принципу передбачається, що всі частинні диференціали

однаково впливають на утворення загальної абсолютної похибки функції .

Нехай величина граничної абсолютної похибки задана. Тоді на підставі формули (1.3)

Припускаючи, що всі доданки рівні між собою, матимемо

.

Звідси

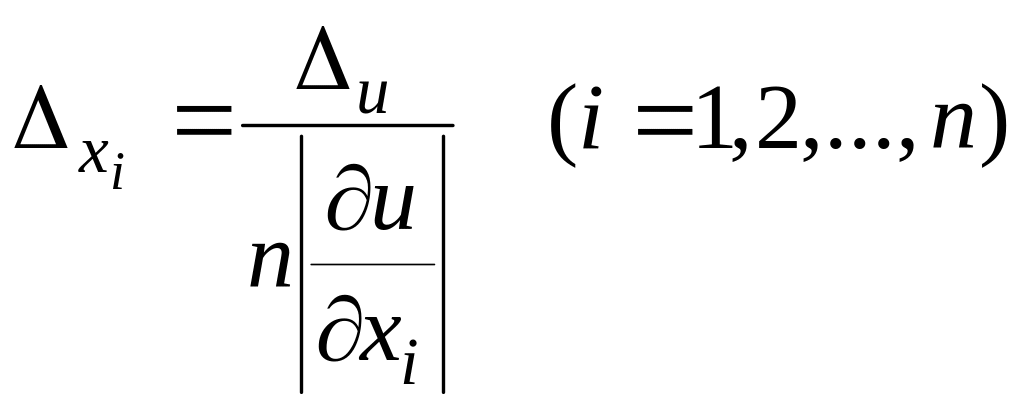(1.6)

Приклад 1. Радіус основи циліндра м; висота циліндра м. З якими абсолютними похибками потрібно визначити R і H, щоб об'єм циліндра V можна було обчислити з точністю до .

Розв’язок. Маємо і .

Вважаючи R = 2м; H = 3м; приблизно отримаємо:

Звідси, оскільки n = 3, то на підставі формули (1.6) матимемо:

1.3 Джерела похибок обчислень

На деяких етапах розв’язування задачі на ЕОМ можуть виникати похибки, які спотворюють результати обчислень. Оцінка ступеня достовірності отриманих результатів є найважливішим питанням при організації обчислювальних робіт. Це особливо важливо за відсутності дослідних або інших даних для порівняння, які могли б в деякій мірі показати надійність чисельного методу, що використовується, і достовірність отриманих результатів.

Розглянемо джерела похибок на окремих етапах розв’язування задачі.

1. Математична модель, прийнята для опису даного процесу або явища, може внести істотні похибки, якщо в ній не враховані які-небудь важливі риси даної задачі. Зокрема, математична модель може чудово працювати в одних умовах і бути абсолютно неприйнятною в інших; тому важливо правильно враховувати область її застосування.

2. Початкові дані задачі часто є основним джерелом похибок. Це так звані неусувні похибки, оскільки вони не можуть бути зменшені обчислювачем ні до початку розв’язування задачі, ні в процесі її розв’язування. Проведений раніше аналіз оцінки похибок при виконанні арифметичних операцій показує, що слід прагнути того, щоб всі початкові дані були приблизно однакової точності. Істотне уточнення одних початкових даних за наявності великих похибок в інших, як правило, не приводить до підвищення точності результатів.

3. Чисельний метод також є джерелом похибок. Це пов'язано, наприклад, із заміною інтеграла сумою, усіканням рядів при обчисленнях значень функцій, інтерполяцією табличних даних тощо. Як правило, похибка чисельного методу регульована, тобто вона може бути зменшена до будь-якого розумного значення шляхом зміни деякого параметра (наприклад, кроку інтеграції, числа членів усіченого ряду тощо). Похибку методу звичайно прагнуть довести до величини, у декілька разів меншої похибки початкових даних. Подальше зниження похибки не приведе до підвищення точності результатів, а лише збільшить вартість розрахунків через необґрунтоване збільшення об'єму обчислень. Докладніше похибки методів розглядатимемо при аналізі конкретних чисельних методів.

4. При обчисленнях за допомогою ЕОМ неминучі похибки округлень, пов'язані з обмеженістю розрядної сітки машини. Звичайно після виконання операції проводиться не округлення результату, а просте відкидання зайвих розрядів з метою економії машинного часу. Правда, в сучасних машинах передбачена свобода вибору програмістом способу округлення; відповідні засоби має в своєму розпорядженні більшість алгоритмічних мов.

Максимальна відносна похибка при округленні є , де  — основа системи числення, k – кількість розрядів мантиси числа. При простому відкиданні зайвих розрядів ця похибка збільшується удвічі.

Не дивлячись на те, що при рішенні великих задач виконуються мільярди операцій, це зовсім не означає механічного множення похибки при одному округленні на число операцій, оскільки при окремих діях похибки можуть компенсувати одна одну (наприклад, при складанні чисел різних знаків). Разом з тим, іноді похибки округлень в поєднанні з погано організованим алгоритмом можуть сильно спотворити результати.

5. Переведення чисел з однієї системи числення в іншу також може бути джерелом похибки через те, що основа однієї системи числення не є ступенем основи іншої (наприклад, 10 і 2), Це може привести до того, що в новій системі числення число стає ірраціональним.

Наприклад, число 0,1 при перекладі в двійкову систему числення приймає вигляд 0,1 = 0,00011001100... Може виявитися, що якщо з кроком 0,1 потрібно при обчисленнях пройти відрізок [0; 1] від х = 1 до х = 0, то десять кроків не дадуть точного значення х = 0.