2.2 Наближене знаходження сум числових рядів

Означення. Числовий ряд

(2.5)

називається збіжним, якщо існує границя послідовності його часткових сум

, (2.6)

де

.

Число називається сумою ряду.

Таким чином, збіжність ряду (2.5) еквівалентна збіжності послідовності його часткових сум. Відповідно до критерію Коші ця послідовність сходиться тоді й тільки тоді, коли для кожного існує таке, що

при та довільному . З формули (2.6) одержуємо:

(2.7)

де – залишок ряду, причому при .

Для знаходження суми збіжного ряду (2.5) із заданою точністю потрібно вибрати число доданків настільки великим, щоб мала місце нерівність

. (2.8)

Тоді часткова сума приблизно може бути прийнята за точну суму ряду (2.5).

Для оцінки залишку ряду (2.5)

корисні наступні теореми, які ми приводимо без доведення.

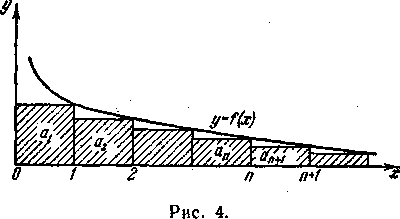
Рис. 2.2

Теорема 1. Якщо члени ряду (2.5) являють собою відповідні значення додатної монотонно спадної функції , тобто

(2.9)

то (рис. 2.2)

.

Теорема 2. Якщо ряд (2.5) – знакозмінний:

і модулі його членів монотонно спадають, то

та

.

Приклад. Знайти суму ряду

(2.10)

з точністю до 0,01.

Розв’язок

Члени ряду (2.10) являють собою відповідні значення монотонно спадної функції

.

Тому для -го залишку ряду

маємо оцінку

.

Розв’язуючи нерівність

,

одержимо:

.

Приймемо .

Матимемо:

.

2.3 Обчислення значень аналітичної функції

Дійсна функція називається аналітичною в точці , якщо в деякому околі цієї точки функція розкладається в степеневий ряд (ряд Тейлора):

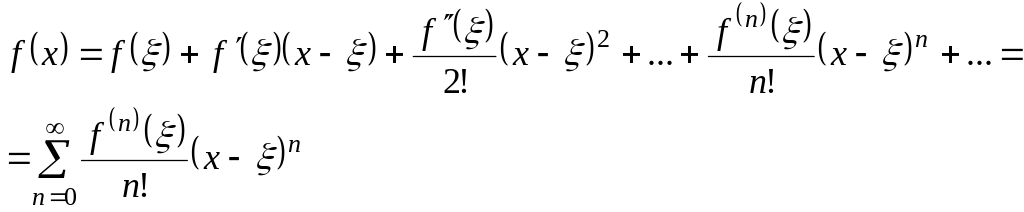(2.11).

При = 0 одержуємо ряд Маклорена

(2.12)

Різниця

називається залишковим членом й являє собою похибку при заміні функції поліномом Тейлора

.

Як відомо,

, (2.13)

де (грецька буква «тета»).

Зокрема, для ряду Маклорена (2.12) маємо:

. (2.14)

Є також інші форми запису залишкових членів.

Розклад функції в ряд Тейлора в багатьох випадках є зручним способом обчислення значень цієї функції.

Якщо відомо й потрібно знайти значення , де — «мале відхилення», то формулу (2.11) вигідно записувати у вигляді

, (2.15)

де

.

Приклад. Приблизно обчислити .

Розв’язок. Маємо:

(2.16)

Поклавши

,

послідовно одержимо:

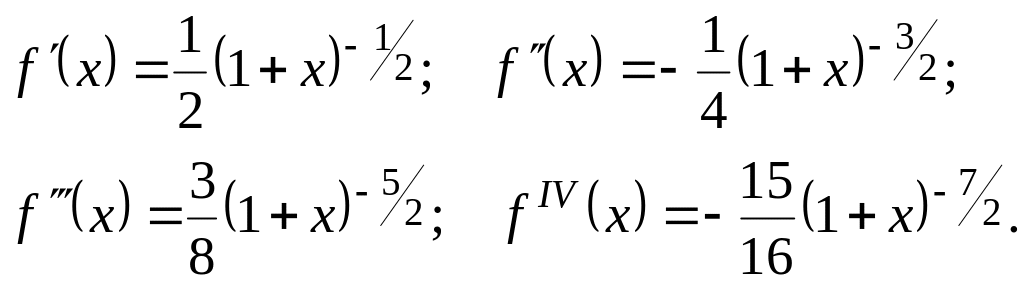
Звідси, прийнявши , і з огляду на те, що

у силу формули (5) знаходимо:

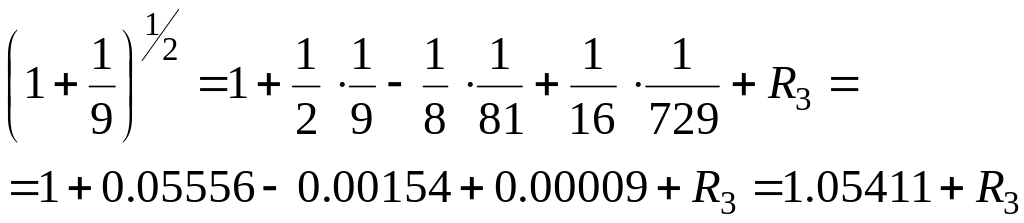, (2.17)

де

.

Очевидно

.

Округляючи до чотирьох знаків, запишемо:

.

Для порівняння приводимо табличне значення:

2.4 Обчислення значень показової функції

Для експонентної функції справедливий розклад

, (2.18)

інтервал збіжності якого .

Залишковий член ряду (2.18) має вигляд

. (2.19)

При більших від одиниці по модулю значеннях ряд (2.18) мало придатний для обчислень. Тому звичайно діють у такий спосіб: нехай

,

де — ціла частина числа та — дробова частина його.

Маємо:

(2.20)

Перший множник добутку (2.20) може бути знайдений за допомогою множення:

якщо ,

або

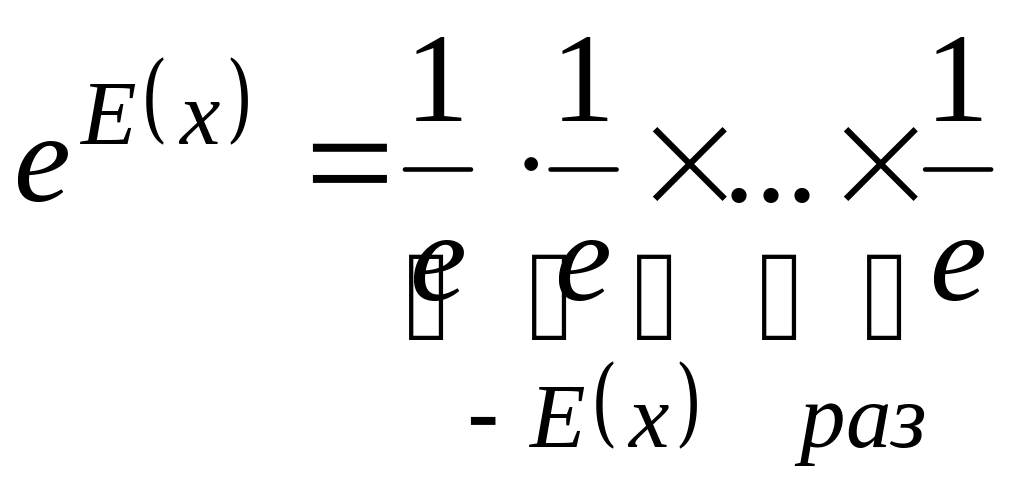якщо .

Тут

причому або , для забезпечення заданої точності, варто взяти з досить великим числом десяткових знаків (у наш час число визначене з понад 300 десятковими знаками).

Що стосується другого множника добутку (2.20), то для обчислення його користуються наведеним вище розкладом

, (2.21)

який при утворює швидко збіжний ряд, тому що на підставі формули (2.19) для залишкового члена маємо оцінку

. (2.22)

Можна вивести (спробуйте це зробити самостійно) більш точну формулу для оцінки залишку при :

. (2.23)

Якщо похибка задана, то необхідне число членів можна знайти підбором, розв’язуючи нерівність

.

Можна довести, що якщо — задана припустима залишкова похибка й , то процес підсумовування варто припинити, як тільки буде виконана нерівність

,

де .

Іншими словами, процес підсумовування припиняється, якщо останній обчислений член по модулю не перевищує , при цьому

.

Приклад 1. Знайти з точністю до .

Розв’язок.

Послідовно маємо:

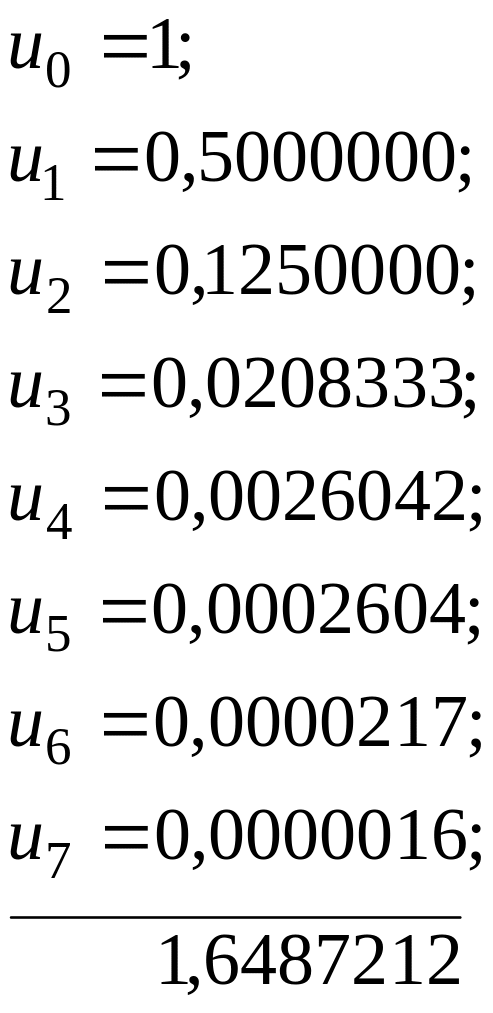
Округляючи суму до п'яти десяткових знаків після коми, одержимо:

, (2.24)

з похибкою .

Для обчислення значень загальної показової функції ( ) можна використати формулу

.