
- •1 Основні поняття теорії похибок
- •1.1 Поняття похибки
- •1.2 Дії над наближеними числами
- •1.3 Пряма та обернена задачі теорії похибок
- •1.3 Джерела похибок обчислень
- •2 Обчислення значень функцій
- •2.1 Обчислення значень полінома. Схема Горнера
- •2.2 Наближене знаходження сум числових рядів
- •2.3 Обчислення значень аналітичної функції
- •2.4 Обчислення значень показової функції
- •2.5 Обчислення значень логарифмічної функції
- •2.6 Обчислення значень тригонометричних функцій
- •3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •3.1 Концепція методів
- •3.2 Метод простої ітерації
- •3.3 Метод Гаусса-Зейделя
- •4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь
- •1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.
- •2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .
- •4.1 Відділення коренів
- •4.2 Метод половинного поділу (метод дихотомії)
- •4.3 Метод хорд (спосіб пропорційних частин)
- •4.4 Метод Ньютона (метод дотичних)
- •4.5 Комбінований метод
- •4.6 Метод ітерації
- •4.7 Метод ітерації для системи двох рівнянь
- •5 Обробка емпіричних даних
- •5.1 Інтерполяція та екстраполяція
- •5.2 Концепція інтерполяції та екстраполяції
- •5.3 Лінійна і квадратична локальні інтерполяції
- •5.4 Глобальна інтерполяція. Многочлен Лагранжа
- •5.5 Глобальна інтерполяція. Многочлен Ньютона
- •5.6 Апроксимація
- •При цьому вимагається, щоб
- •Побудуємо емпіричний точковий графік.
- •Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
- •6 Наближене обчислення визначених інтегралів
- •6.1 Концепція чисельного інтегрування
- •6.2 Методи прямокутників та трапецій
- •6.3 Метод Симпсона
- •6.4 Метод Монте-Карло
2.5 Обчислення значень логарифмічної функції
Для натуральних логарифмів чисел, близьких до одиниці, справедливий розклад:
![]() .
(2.25)
.
(2.25)
Формула
(2.25) малопридатна для обчислень, тому
що діапазон чисел
![]() невеликий та, крім того, при
невеликий та, крім того, при
![]() ,
близькому до одиниці, ряд (2.25) сходиться
повільно.
,
близькому до одиниці, ряд (2.25) сходиться
повільно.
Уведемо
більше зручну формулу для обчислень
натуральних логарифмів чисел. Для
цього скористаємося аналогом формули
(2.25) для
![]() ,
а також зробимо заміну
,
а також зробимо заміну
![]() .
(2.26)
.
(2.26)
Одержимо (спробуйте це зробити самостійно) формулу:
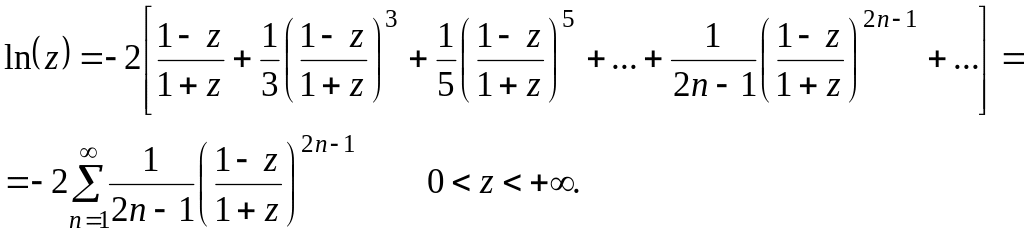 (2.27)
(2.27)
Нехай - додатне число. Представимо його у вигляді
![]() ,
,
де
![]() - ціле
число та
- ціле
число та
![]() .
Тоді, поклавши
.
Тоді, поклавши
![]() ,
,
де
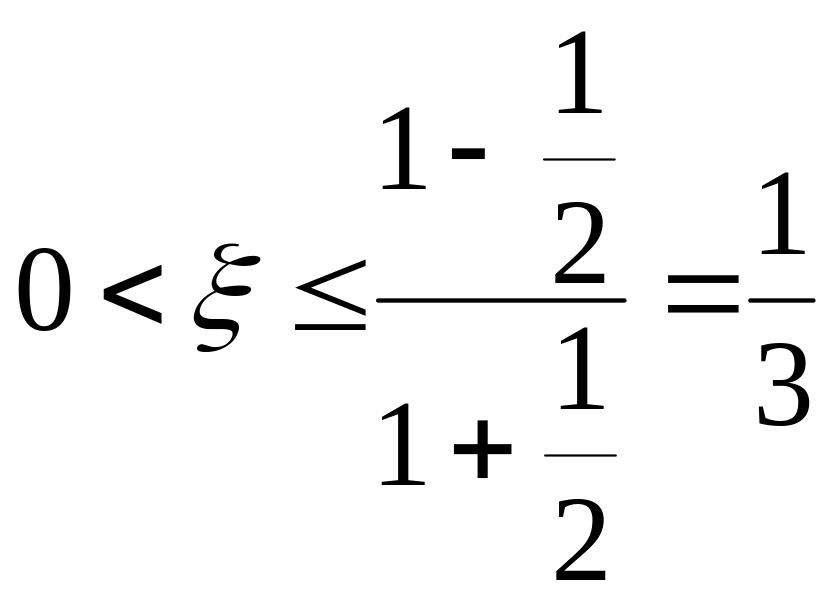 ,
,
і застосовуючи формулу (2.27), будемо мати:
![]() .
.
![]()
Застосувавши позначення
![]() ,
,
одержимо:
![]() .
(2.28)
.
(2.28)
Можна показати, що при заданій точності процес підсумовування припиняється (досягається необхідна точність), як тільки
![]() ,
,
де
![]() .
.
Приклад.
Знайти
![]() з точністю до
.
з точністю до
.
Розв’язок. Обчислення будемо виконувати із двома запасними знаками. Покладемо
![]() .
.
Звідси
![]() ,
,
![]() і
і
![]()
Маємо:
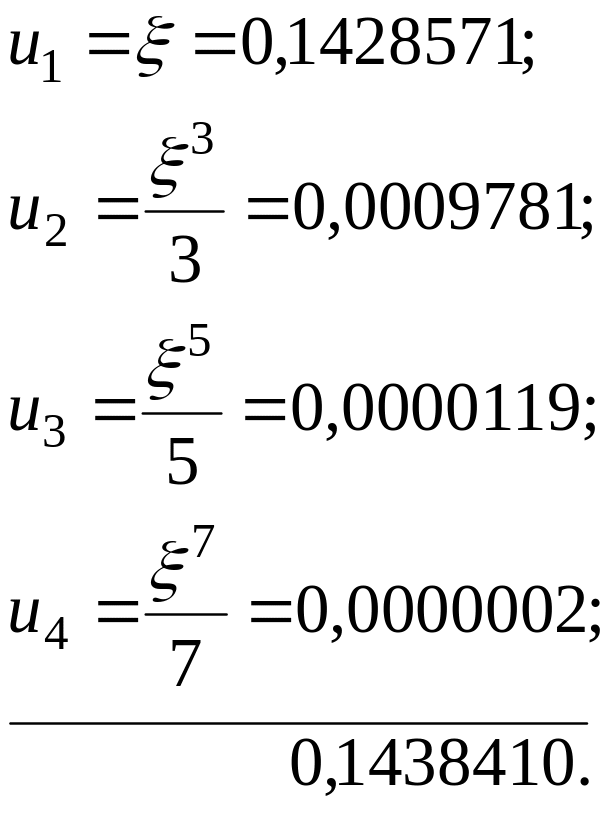
Використовуючи формулу (2.28), одержуємо:
![]() .
.
Зауваження. Можна також обчислювати натуральні логарифми чисел, виходячи з представлення числа :
![]() ,
,
де
![]() - ціле число та
- ціле число та
![]() .
.
Для обчислення десяткових логарифмів використовується формула
![]() ,
,
де
![]() .
.
2.6 Обчислення значень тригонометричних функцій
Обчислення значень синуса й косинуса.
За
допомогою формул приведення аргумент
можна укласти у відрізок
![]() .
Якщо
.
Якщо
![]() ,
то маємо:
,
то маємо:
![]() ,
(2.29)
,
(2.29)
якщо
ж
![]() ,
то покладемо
,
то покладемо
![]() ,
(2.30)
,
(2.30)
де
![]() та
та
![]() .
.
Тому що ряд (2.29) знакозмінний з монотонно спадними, по модулю, членами, то для залишкового члена справедлива оцінка
![]() та
та
![]()
Тому процес підсумовування можна припинити, як тільки буде виявлено, що
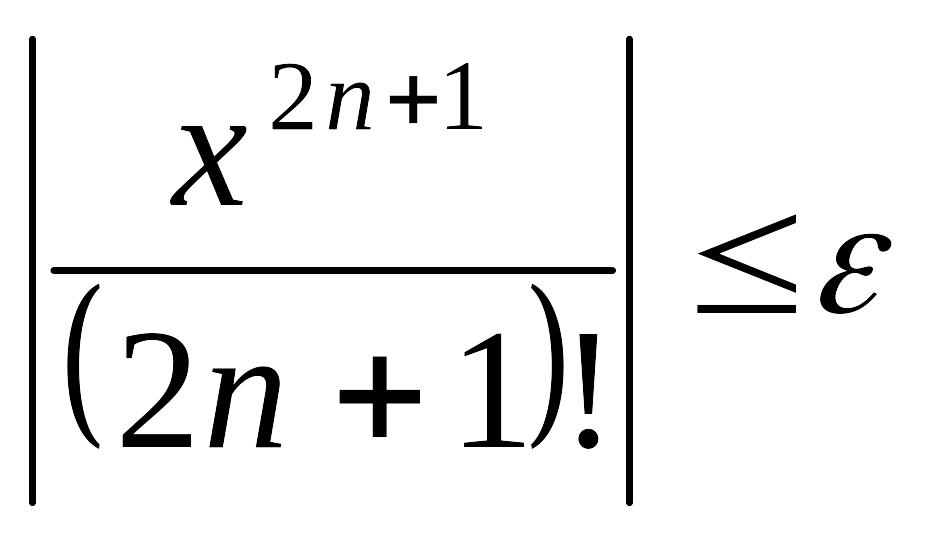 ,
,
де - задана залишкова похибка.
Аналогічно здійснюється обчислення інших тригонометричних функцій.
Приклад.
Знайти
![]() з точністю до
.
з точністю до
.
Розв’язок.
Переведемо величину
![]() в радіани. Маємо:
в радіани. Маємо:
![]() .
.
Застосовуючи формулу (2.29), одержимо:
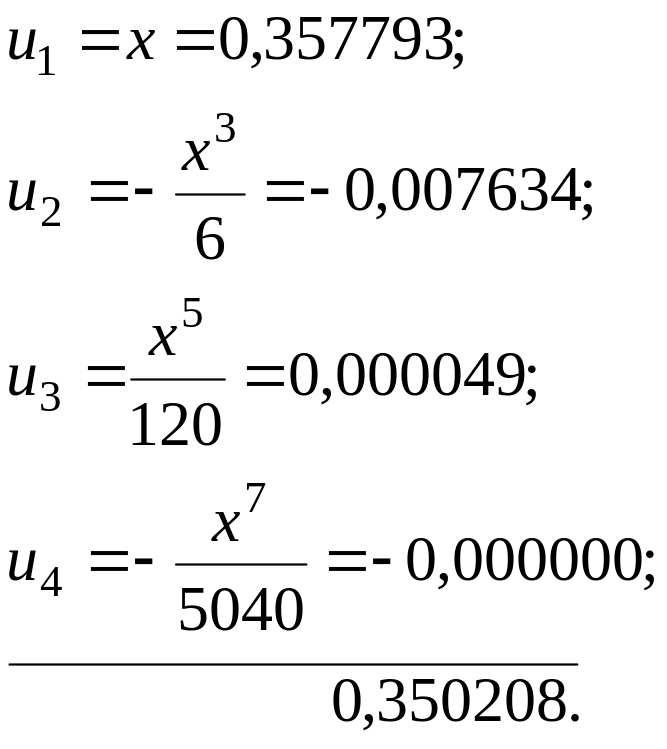
Звідси
![]()
3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
Системи лінійних алгебраїчних рівнянь в обчисленнях мають дуже велике значення, оскільки до них зводиться наближене розв’язування широкого кола обчислювальних задач, у тому числі систем нелінійних алгебраїчних рівнянь і диференціальних рівнянь. Теорія розв’язування лінійних систем достатньо розроблена, є велика кількість різноманітних програмних засобів для розв’язування самих різних систем рівнянь: обумовлених, блочних, стрічкових, з розрідженими матрицями тощо. Тому тут детально не розглядатимемо всі методи, а згадаємо лише основні ідеї і їх особливості.
3.1 Концепція методів
Методи розв’язування СЛАР звичайно розділені на дві великі групи: точні (або прямі) і наближені (ітераційні).
Точні (прямі) методи дозволяють для будь-яких систем у принципі знайти точні значення невідомих після скінченого числа арифметичних операцій, кожна з яких виконується точно.
Наближені ітераційні методи дають розв’язок в результаті, у принципі, нескінченного процесу наближень.
З прямих методів найбільш поширені методи Гауса, Крамера і LU-перетворення, набагато рідше використовується метод оберненої матриці. Метод Крамера (з використанням визначників) вимагає дуже великих обчислень вже при розв’язуванні системи 5 рівнянь, тому використовується тільки в учбовій літературі.
З ітераційних методів використовуються в основному методи простої ітерації і метод Гаусса-Зейделя.
Прямі методи вивчалися у курсі «Вища математика». Тому одразу переходимо до вивчення ітераційних методів.
