
- •1 Основні поняття теорії похибок
- •1.1 Поняття похибки
- •1.2 Дії над наближеними числами
- •1.3 Пряма та обернена задачі теорії похибок
- •1.3 Джерела похибок обчислень
- •2 Обчислення значень функцій
- •2.1 Обчислення значень полінома. Схема Горнера
- •2.2 Наближене знаходження сум числових рядів
- •2.3 Обчислення значень аналітичної функції
- •2.4 Обчислення значень показової функції
- •2.5 Обчислення значень логарифмічної функції
- •2.6 Обчислення значень тригонометричних функцій
- •3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •3.1 Концепція методів
- •3.2 Метод простої ітерації
- •3.3 Метод Гаусса-Зейделя
- •4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь
- •1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.
- •2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .
- •4.1 Відділення коренів
- •4.2 Метод половинного поділу (метод дихотомії)
- •4.3 Метод хорд (спосіб пропорційних частин)
- •4.4 Метод Ньютона (метод дотичних)
- •4.5 Комбінований метод
- •4.6 Метод ітерації
- •4.7 Метод ітерації для системи двох рівнянь
- •5 Обробка емпіричних даних
- •5.1 Інтерполяція та екстраполяція
- •5.2 Концепція інтерполяції та екстраполяції
- •5.3 Лінійна і квадратична локальні інтерполяції
- •5.4 Глобальна інтерполяція. Многочлен Лагранжа
- •5.5 Глобальна інтерполяція. Многочлен Ньютона
- •5.6 Апроксимація
- •При цьому вимагається, щоб
- •Побудуємо емпіричний точковий графік.
- •Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
- •6 Наближене обчислення визначених інтегралів
- •6.1 Концепція чисельного інтегрування
- •6.2 Методи прямокутників та трапецій
- •6.3 Метод Симпсона
- •6.4 Метод Монте-Карло
5.3 Лінійна і квадратична локальні інтерполяції
Найпростішим
видом локальної інтерполяції є лінійна
інтерполяція. Вона полягає в тому, що
задані точки
![]() з'єднуються
прямолінійними
відрізками, а функція
апроксимується
ламаною
з вершинами в даних точках.
з'єднуються
прямолінійними
відрізками, а функція
апроксимується
ламаною
з вершинами в даних точках.
Для
і-го
інтервалу
можна написати рівняння прямої, що
проходить через точки
![]() та
та
![]() у вигляді:
у вигляді:
![]() .
.
Звідси
![]() (5.2)
(5.2)
Для
визначення наближеного значення ![]() в середині будь-якого інтервалу, спочатку
по значенню x
визначають
інтервал, а потім підставляють x
в
рівняння цього інтервалу.
в середині будь-якого інтервалу, спочатку
по значенню x
визначають
інтервал, а потім підставляють x
в
рівняння цього інтервалу.
Для
випадку квадратичної інтерполяції як
інтерполяційний многочлен на відрізку
![]() приймається квадратний многочлен
приймається квадратний многочлен
![]() .
.
Тут
невідомими є
![]() вони
знаходяться з умови проходження
многочлена через три точки
вони
знаходяться з умови проходження
многочлена через три точки
![]()
![]() .
(5.3)
.
(5.3)
Інтерполяція
для будь-якої точки х
з
інтервалу ![]() проводиться
по
трьох найближчих
до
неї вузлах.
проводиться
по
трьох найближчих
до
неї вузлах.
На рис. 5.2 показано графіки локальних (лінійної та квадратичної) інтерполяційних функцій.
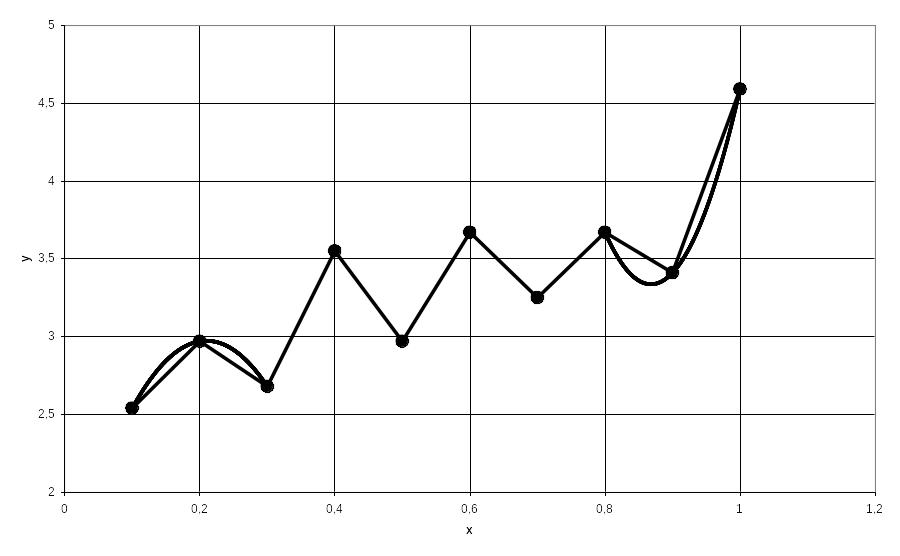
Рис. 5.2 – Лінійна та квадратична інтерполяція
Приклад:
Знайти наближене значення функції ![]() при
х=0,32,
якщо відома таблиця її значень:
при
х=0,32,
якщо відома таблиця її значень:
х |
0,15 |
0,30 |
0,4 |
0,55 |
у |
2,17 |
3,63 |
5,07 |
7,78 |
а) При лінійній інтерполяції х=0,32 знаходиться між вузлами 0,3 і 0,4. В цьому випадку
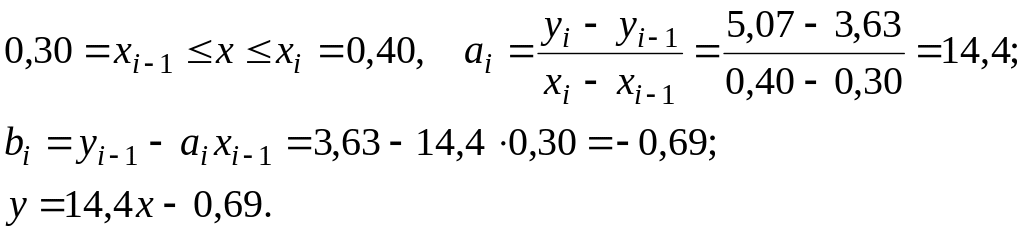
При
![]() маємо (рис. 5.3):
маємо (рис. 5.3):
![]() .
.
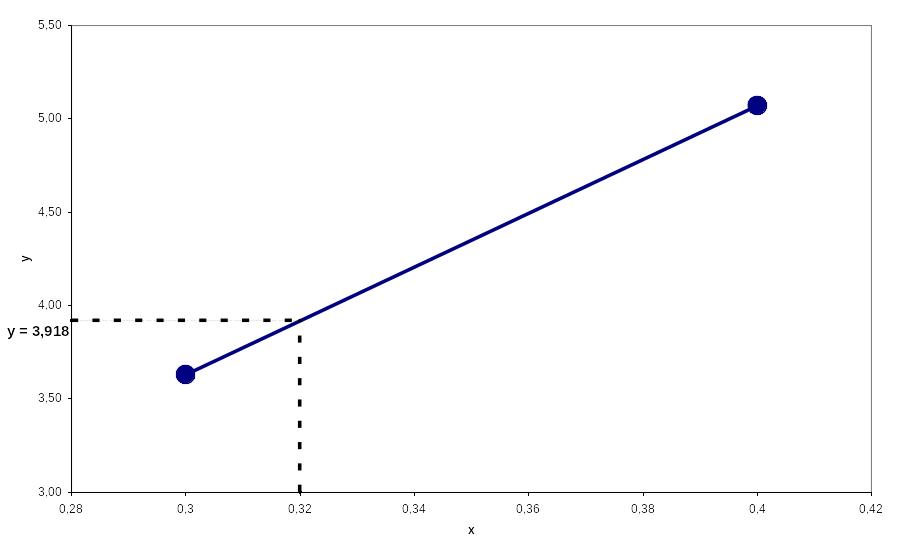
Рис. 5.3 – Лінійна локальна інтерполяція
б) При квадратичній інтерполяції складемо систему рівнянь для найближчих до точки х=0.32 вузлів:
![]()
відповідно
![]()
Маємо систему рівнянь:
![]()
Розв’язуючи цю систему, знаходимо:
![]()
Отже, інтерполяційна квадратична функція:
![]()
Тоді
шукане значення
![]() в
точці х=0,32
буде
(рис. 5.4):
в
точці х=0,32
буде
(рис. 5.4):
![]() .
.
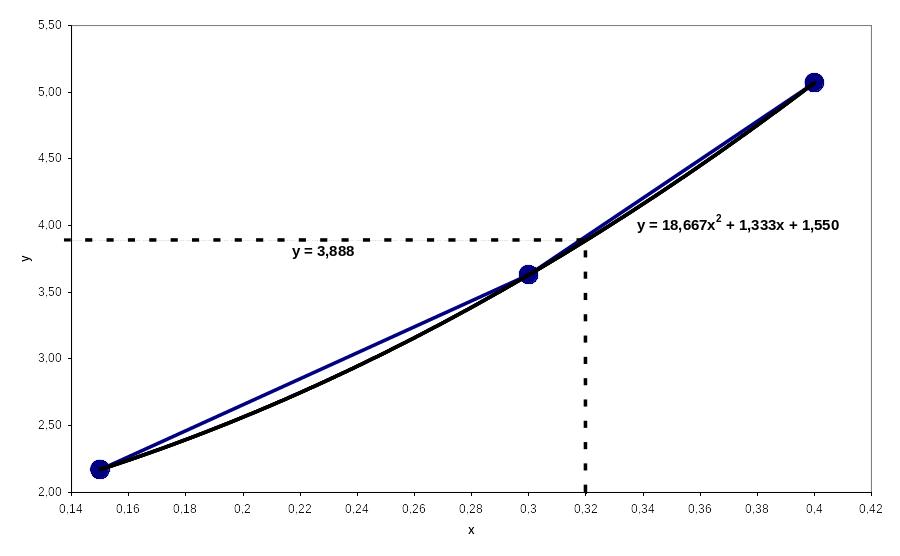
Рис. 5.4 – Квадратична локальна інтерполяція
5.4 Глобальна інтерполяція. Многочлен Лагранжа
Нехай
відомі значення функції
в
![]() точках
точках
![]() .
Для
інтерполяції функції в довільній точці
,
що належить
відрізку
.
Для
інтерполяції функції в довільній точці
,
що належить
відрізку
![]() ,
необхідно
побудувати
інтерполяційний поліном n-го порядку,
який в методі Лагранжа має вигляд:
,
необхідно
побудувати
інтерполяційний поліном n-го порядку,
який в методі Лагранжа має вигляд:
![]() (5.4)
(5.4)
де
![]()
Якщо розкрити добутки всіх дужок в чисельнику (в знаменнику всі дужки є числами), то отримаємо поліном n-го порядку від х, тобто в чисельнику n співмножників першого порядку. Наступний поліном Лагранжа не що інше, як звичайний поліном n-го порядку, але записаний в іншій формі. Підставляючи l(x) у вираз для L(x), отримаємо
![]() (5.5)
(5.5)
Неважко помітити, що у вузлах інтерполяції:
![]()
Оцінити
похибку інтерполяції в точці
![]() (друга
проблема інтерполяції) можна по формулі:
(друга
проблема інтерполяції) можна по формулі:
![]() (5.6)
(5.6)
де ![]() - максимальне
значення
- максимальне
значення
![]() -ої
похідної початкової функції f(x)
на
відрізку
.
-ої
похідної початкової функції f(x)
на
відрізку
.
Отже,
щоб оцінити похибку, треба знати
![]() ,
що не завжди можливо.
,
що не завжди можливо.
З
формули (5.5) можна отримати вираз для
лінійної
![]() і
квадратичної
і
квадратичної
![]() інтерполяції
без обчислення відповідних
коефіцієнтів.
інтерполяції
без обчислення відповідних
коефіцієнтів.
5.5 Глобальна інтерполяція. Многочлен Ньютона
У загальному випадку інтерполяція по формулах Ньютона може здійснюватися для довільно розташованих вузлів інтерполяції, але частіше – для рівномірно розташованих вузлів.
Тоді
![]() ,
де
,
де
![]() .
.
Метод використовує поняття скінчених різниць:
![]() - різниці
1-го порядку
- різниці
1-го порядку
![]() -
різниці
2-го порядку
-
різниці
2-го порядку
![]() - різниці
3-го порядку
- різниці
3-го порядку
Для
визначення різниці k
–
го
порядку потрібне знання всіх
точок
від
![]() до
до
![]() :
:
![]() (5.7)
(5.7)
Можна помітити, що за наявності n+1 точок (0,1,2,.., n), скінчену різницю 1-го порядку можна обчислити тільки для перших n точок (0,1,2,....,n –1), скінчену різницю n – го порядку – тільки для нульової точки, а k – го порядку - тільки для перших n - k+1 точок, тобто треба знати k точок попереду. Інтерполяційний многочлен Ньютона записується таким чином:
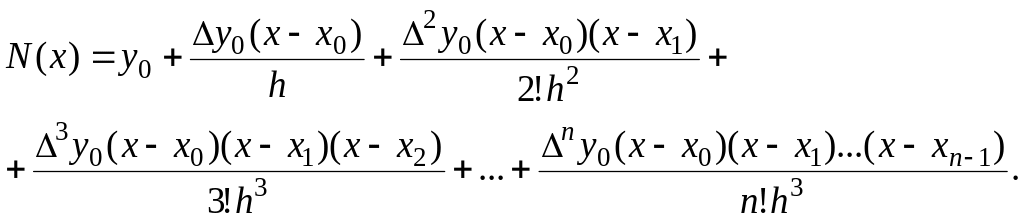 (5.8)
(5.8)
Це теж поліном n – го порядку, якщо виконати відповідні множення, то скінчені різниці у виразі – це числові коефіцієнти, обчислені по заданих точках.
Часто
замість х
вводять
безрозмірну величину q,
що показує, скільки міститься кроків
від
![]() до заданої точки
.
Ця
величина визначається таким чином:
до заданої точки
.
Ця
величина визначається таким чином:
![]() .
.
Тоді
![]() (5.9)
(5.9)
Обидві приведені формули називаються першим інтерполяційним многочленом Ньютона для інтерполяції вперед.
Д![]() ля
інтерполяції в правому кінці відрізка
,
коли для k
останніх
точок не можна обчислити потрібні
скінчені різниці, використовують
многочлен
Ньютона,
в якому скінчені різниці обчислюються
справа наліво, тобто здійснюється
інтерполяція назад. Такий многочлен
називається другим
інтерполяційним
многочленом
Ньютона
для інтерполяції назад.
ля
інтерполяції в правому кінці відрізка
,
коли для k
останніх
точок не можна обчислити потрібні
скінчені різниці, використовують
многочлен
Ньютона,
в якому скінчені різниці обчислюються
справа наліво, тобто здійснюється
інтерполяція назад. Такий многочлен
називається другим
інтерполяційним
многочленом
Ньютона
для інтерполяції назад.
В
цьому випадку ![]()
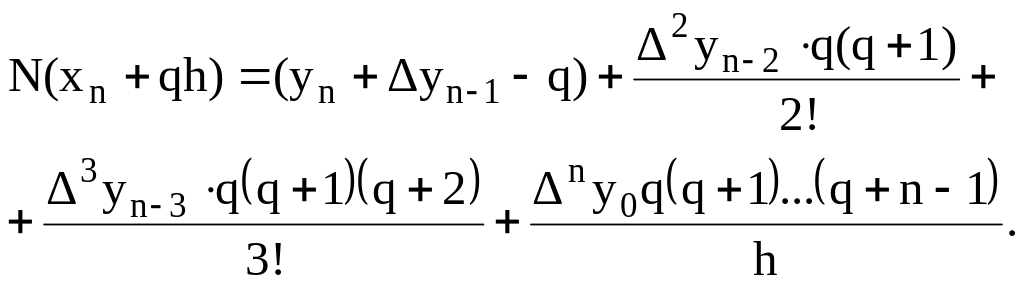 (5.10)
(5.10)
Похибку інтерполяції, як і для многочлена Лагранжа, можна оцінити так:
![]() .
(5.11)
.
(5.11)
Використовування скінчених різниць, що є своєрідними аналогами похідних неперервних функцій, допомагає знаходити похибку інтерполяції, використовуючи співвідношення:
![]() ,
,
![]() ,
,
![]() ,…,
,…,
![]() .
.
Тоді
для отримання наближеного значення
![]() достатньо
мати декілька (або навіть одну) додаткових
точок
достатньо
мати декілька (або навіть одну) додаткових
точок
![]() ,
з використанням яких легко знайти
максимальне значення скінченої різниці
(n+1) –
го
порядку:
,
з використанням яких легко знайти
максимальне значення скінченої різниці
(n+1) –
го
порядку:
![]()
![]() (5.12)
(5.12)
Аналогічно можна знайти похибку і в методі Лагранжа при рівномірному кроці.
Приклад. Задана таблиця значень функцыъ , необхідно знайти у(2,05). Використовуємо для інтерполяції тільки три перші точки, а решту – для оцінок похибки.
Отже, n+1=3, n=2
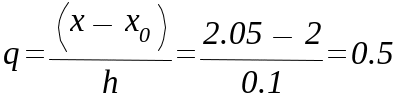
х |
у |
Δy |
Δ²y |
Δ³y |
2,0 |
0,0540 |
-0,0100 |
0,0015 |
-0,0002 |
2,1 |
0.0440 |
-0,0085 |
0,0013 |
0 |
2,2 |
0.0355 |
-0,0072 |
0,0013 |
-0,0003 |
2,3 |
0.0283 |
-0,0057 |
0,0010 |
-0,0001 |
2,4 |
0.0224 |
-0,0049 |
0 |
|
2,5 |
0.0175 |
-0,0049 |
|
|
2,6 |
0.0136 |
|
|
|
Скористаємося першою інтерполяційною формулою Ньютона:
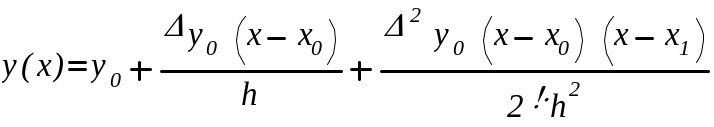
![]()
Оцінимо похибку знайденого значення у. З таблиці знаходимо, що М3=0,001,
тоді
![]()
Формули Лагранжа, Ньютона і інші породжують один і той же многочлен. Різниця лише в алгоритмі їх побудови. Вибір способу інтерполяції визначається різними міркуваннями: точністю, часом обчислень, похибками округлення тощо.
Підвищення
точності інтерполяції доцільно проводити
за рахунок зменшення кроку і спеціального
розташування
вузлових точок
.
Підвищення степеня інтерполяційного
многочлена також підвищує точність,
проте не завжди (залежить від поведінки
похідної
![]() .
Тому на практиці прагнуть використовувати
многочлени малого степеня (лінійний,
квадратичний).
.
Тому на практиці прагнуть використовувати
многочлени малого степеня (лінійний,
квадратичний).
