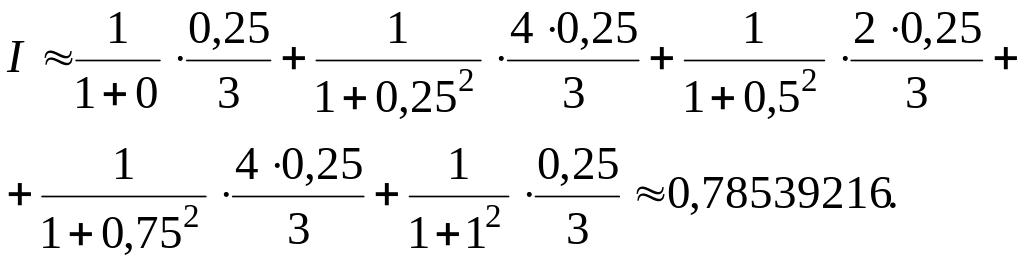6.2 Методи прямокутників та трапецій

Методи прямокутників (лівих і правих) і трапецій можна віднести до найпростіших методів чисельного інтегрування. В першому випадку підінтегральна функція замінюється горизонтальною прямою із значенням ординати (тобто значенням функції) відповідно зліва або справа ділянки, в другому випадку — похилої прямої _.

Формули інтегрування при розбитті відрізка [а,b] на n частин з рівномірним кроком h відповідно набувають вигляд:

- метод лівих прямокутників

,

- метод правих прямокутників

,

- метод трапецій

.

Неважко помітити, що в методі прямокутників інтеграл обчислюється абсолютно точно тільки при , а в методі трапецій – при лінійній або шматково-лінійній.

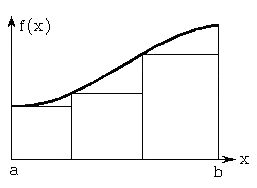
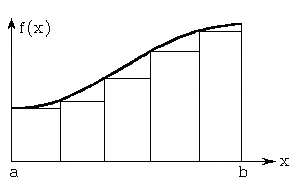
а) б)

а) – з 3 ділянками розбиття відрізка інтегрування [а, b];

б) – з 5 ділянками розбиття відрізка інтегрування [а, b]

Рис. 6.1 – Ілюстрація методу лівих прямокутників

На рис. 6.1 для порівняння наведені приклади прямокутників при різному числі ділянок. Наочно видно, що площа всіх прямокутників на правому малюнку менше відрізняється від площі під кривою , ніж на лівому.

Метод прямокутників не знаходить практичного застосування через значні похибки, що теж видно з рис. 6.1.

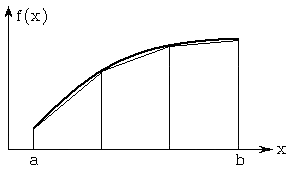
Рис. 6.2 – Ілюстрація методу трапецій

На рис. 6.2 наведений приклад обчислення інтеграла методом трапецій. В порівнянні з методом прямокутників, метод трапецій більш точний, оскільки трапеція точніше замінює відповідну криволінійну трапецію, ніж прямокутник.

Похибка обчислення інтеграла методом трапецій при використовуванні подвійного прорахунку на практиці може бути визначена з наступного співвідношення:

,

де і – відповідно значення інтеграла при числі розбиття і .

Існують і аналітичні вирази для визначення похибки, але вони вимагають знання другої похідної підінтегральної функції, тому мають тільки теоретичне значення. З використанням подвійного прорахунку можна організувати автоматичний підбір кроку інтеграції (тобто числа розбиття ) для забезпечення заданої похибки інтегрування (послідовно подвоюючи крок і контролюючи похибку).

Приклад. Обчислити .

1) для всього інтервалу;

2) з розподілом інтервалу на чотири ділянки.

Аналітичне обчислення даного інтеграла дає

.

В нашому випадку:

1)

2)

.

Обчислимо інтеграл різними методами.

Метод лівих прямокутників:

1) ;

2) .

Метод правих прямокутників:

1) ;

2)

Метод трапецій:

1) ;

2)

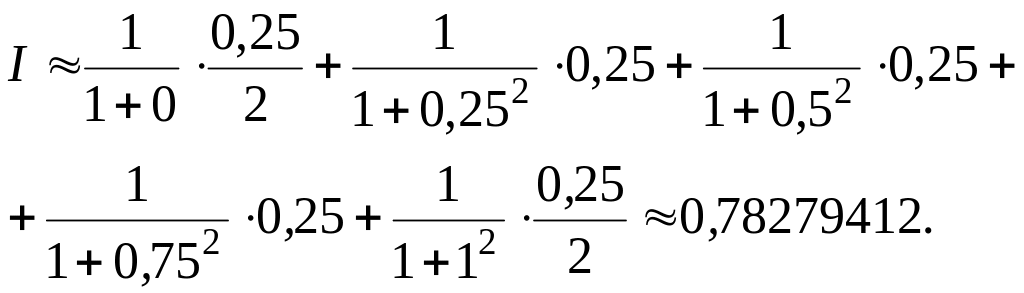
6.3 Метод Симпсона

Цей метод базується на заміні підінтегральної функції квадратичною параболою, яка будується вже не по двох (як пряма в методі трапецій), а по трьох точках на кожній ділянці. По цих трьох точках (крайні точки ділянки і середня точка) будується інтерполяційна функція — поліном другого порядку, який аналітично інтегрується. Виходить наступна розрахункова формула (формула Симпсона):

.

В цій формулі всі ординати з непарними номерами мають коефіцієнт , а з парними – (окрім нульового і останнього). При роботі з цим методом обов'язково розбивають весь інтервал на парне число ділянок.

Метод Симпсона забезпечує обчислення інтеграла точно без похибки для полінома третього порядку. Отже, цей метод більш прийнятний від попередніх. Кількісно оцінити похибку при використовуванні подвійного прорахунку можна по співвідношенню

тобто при збільшенні числа розбиття в два рази погрішність падає в 15 разів.

Теоретичні формули оцінки похибки містять похідну четвертого порядку від підінтегральної функції, тому не мають практичного значення.

Приклад.

Розглянемо обчислення інтеграла з попереднього розділу.

1) При матимемо

.

2) При маємо: