
- •1 Основні поняття теорії похибок
- •1.1 Поняття похибки
- •1.2 Дії над наближеними числами
- •1.3 Пряма та обернена задачі теорії похибок
- •1.3 Джерела похибок обчислень
- •2 Обчислення значень функцій
- •2.1 Обчислення значень полінома. Схема Горнера
- •2.2 Наближене знаходження сум числових рядів
- •2.3 Обчислення значень аналітичної функції
- •2.4 Обчислення значень показової функції
- •2.5 Обчислення значень логарифмічної функції
- •2.6 Обчислення значень тригонометричних функцій
- •3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •3.1 Концепція методів
- •3.2 Метод простої ітерації
- •3.3 Метод Гаусса-Зейделя
- •4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь
- •1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.
- •2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .
- •4.1 Відділення коренів
- •4.2 Метод половинного поділу (метод дихотомії)
- •4.3 Метод хорд (спосіб пропорційних частин)
- •4.4 Метод Ньютона (метод дотичних)
- •4.5 Комбінований метод
- •4.6 Метод ітерації
- •4.7 Метод ітерації для системи двох рівнянь
- •5 Обробка емпіричних даних
- •5.1 Інтерполяція та екстраполяція
- •5.2 Концепція інтерполяції та екстраполяції
- •5.3 Лінійна і квадратична локальні інтерполяції
- •5.4 Глобальна інтерполяція. Многочлен Лагранжа
- •5.5 Глобальна інтерполяція. Многочлен Ньютона
- •5.6 Апроксимація
- •При цьому вимагається, щоб
- •Побудуємо емпіричний точковий графік.
- •Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
- •6 Наближене обчислення визначених інтегралів
- •6.1 Концепція чисельного інтегрування
- •6.2 Методи прямокутників та трапецій
- •6.3 Метод Симпсона
- •6.4 Метод Монте-Карло
4.5 Комбінований метод
Нехай
![]() ,
і
зберігають сталі знаки на відрізку
.
Об’єднуючи методи хорд та Ньютона,
отримаємо метод, на кожному етапі якого
знаходимо значення з нестачею
та значення з надлишком
,
і
зберігають сталі знаки на відрізку
.
Об’єднуючи методи хорд та Ньютона,
отримаємо метод, на кожному етапі якого
знаходимо значення з нестачею
та значення з надлишком
![]() точного кореня
рівняння
.
точного кореня
рівняння
.
Звідси, зокрема, випливає, що цифри, спільні для і , обов’язково належать точному кореню . Теоретично можливі чотири випадки:
1)
![]() (мал. 4.7);
(мал. 4.7);
2)
![]() (мал. 4.8);
(мал. 4.8);
3)
![]() (мал. 4.9);
(мал. 4.9);
4)
![]() (мал. 4.10 ).
(мал. 4.10 ).
Ми
обмежимося розглядом першого випадку.
Інші випадки вивчаються аналогічно,
причому характер обчислень легко
зрозуміти з відповідних малюнків.
Зауважимо, що ці випадки можна звести
до першого, якщо замінити досліджуване
рівняння
![]() рівносильними йому рівняннями:
рівносильними йому рівняннями:
![]() та
та
![]() ,
де
,
де
![]() .
.
Отже,
нехай
та
при
.
Покладемо
![]() та
та
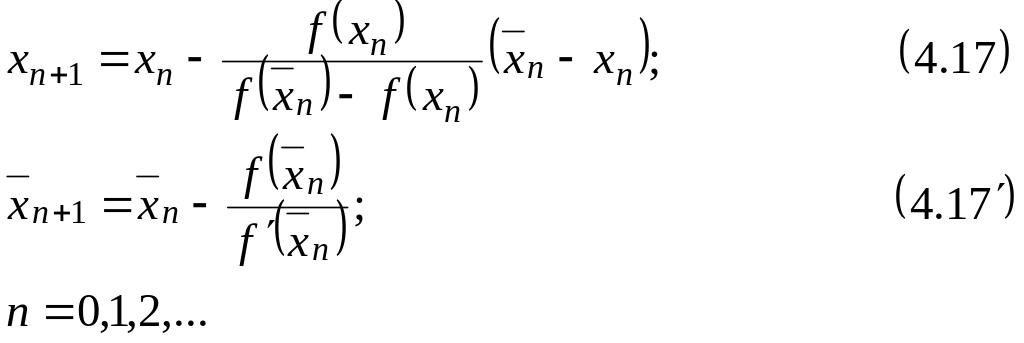

Рис. 4.7 Рис. 4.8
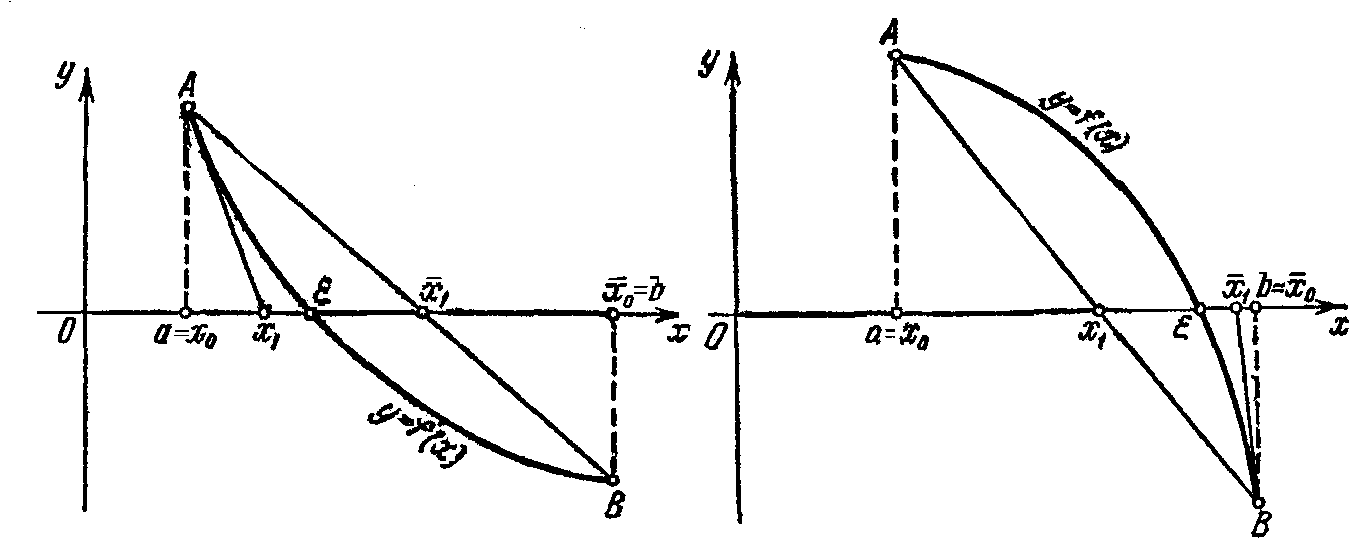
Рис. 4.9 Рис. 4.10
У
формулах
![]() та
та
![]() метод хорд застосовується на кожному
кроці до нового відрізка
метод хорд застосовується на кожному
кроці до нового відрізка
![]() .
.
Легко встановити, що
![]() (4.18).
(4.18).
Отже,
якщо абсолютна похибка наближеного
кореня
задана попередньо і рівна
,
то процес зближення закінчується тоді,
коли буде встановлено, що
![]() .
По закінченню процесу значення кореня
краще всього прийняти рівним середньому
арифметичному знайдених останніх
значень:
.
По закінченню процесу значення кореня
краще всього прийняти рівним середньому
арифметичному знайдених останніх
значень:
![]() .
.
Приклад.
Обчислити з точністю
![]() єдиний додатний корінь рівняння
єдиний додатний корінь рівняння
![]() .
.
Розв’язок.
Так як
![]() і
і
![]() ,
то корінь знаходиться в інтервалі
,
то корінь знаходиться в інтервалі
![]() .
Маємо:
.
Маємо:
![]() та
та
![]() .
.
У вибраному нами інтервалі перша та друга похідні зберігають додатний знак.
Застосуємо
комбінований метод, поклавши
![]() та
та
![]() .
.
Обчислення за формулами та дадуть такі результати:
![]() .
.
Так
як
![]() ,
обчислення потрібно продовжити. Знаходимо
наступну пару наближень:
,
обчислення потрібно продовжити. Знаходимо
наступну пару наближень:
![]() .
.
Так
як
![]() ,
обчислення слід закінчити.
,
обчислення слід закінчити.
Можна покласти:
![]() .
.
4.6 Метод ітерації
Одним з найбільш важливих методів чисельного розв’язування рівнянь є метод ітерації ( часто метод ітерації називають методом послідовних наближень). Сутність цього методу полягає у наступному.
Нехай дано рівняння
(4.19),
де — неперервна функція, і потрібно знайти його дійсні корені.
Замінимо рівняння (4.19) рівносильним рівнянням
![]() .
(4.20)
.
(4.20)
Виберемо яким-небудь способом наближене значення кореня та підставимо його у праву частину рівняння (4.20). Тоді отримаємо деяке число
![]() .
(4.21)
.
(4.21)
Підставимо
тепер у праву частину рівності (4.20)
замість
число
,
отримаємо нове число
![]() .
Повторюючи цей процес, отримаємо
послідовність чисел
.
Повторюючи цей процес, отримаємо
послідовність чисел
![]() .
(4.22)
.
(4.22)
Якщо
ця послідовність — збіжна, тобто існує
границя
![]() ,
то, переходячи до границі у рівності
(4.22) и вважаючи функцію
,
то, переходячи до границі у рівності
(4.22) и вважаючи функцію
![]() неперервною, знаходимо:
неперервною, знаходимо:
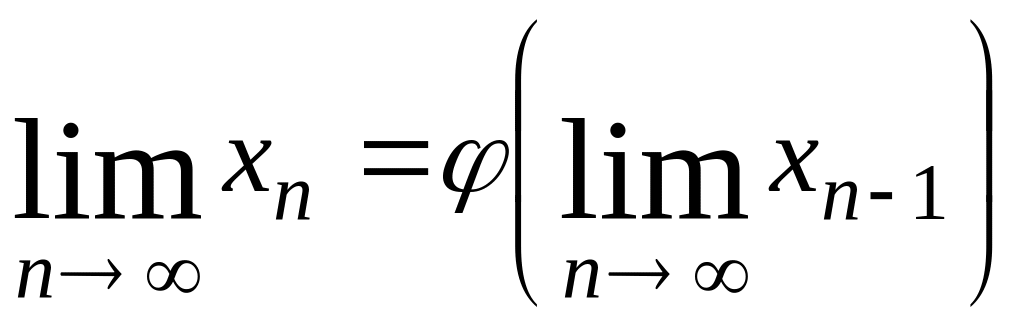
або
![]() (4.23).
(4.23).
Таким чином, границя є коренем рівняння (4.20) и може бути обчислена за формулою (4.22) з будь-якою точністю.
Для практичного застосування методу ітерації потрібно з’ясувати достатні умови збіжності ітераційного процесу.
Теорема
1 (без доведення). Нехай функція
визначена і диференційована на відрізку
,
причому всі її значення
![]() .
.
Тоді,
якщо існує дійсне число
![]() таке, що
таке, що
![]() (4.24)
(4.24)
при , то:
1) процес ітерації
![]()
збігається
незалежно від початкового значення
![]() ;
;
2) граничне значення
є єдиним коренем рівняння
.
Зауваження
1. Теорема залишається справедливою,
якщо функція
визначена та диференційована на
нескінченому інтервалі
,
причому при
![]() виконується нерівність (4.24).
виконується нерівність (4.24).
Зауваження 2. В умовах теореми 1 метод ітерації збігається при будь-якому виборі початкового значення . Завдяки цьому цей метод є таким, що сам виправляється, тобто, окрема помилка у обчисленнях, яка не виводить за межі відрізка , не вплине на кінцевий результат, адже помилкове значення можна розглядувати як нове початкове значення . Можливо, зросте лише обсяг роботи. Властивість самовиправлення робить метод ітерації одним з надійніших методів обчислення. Звичайно, систематичні помилки при застосуванні методу ітерації можуть завадити отриманню правильного результату.
Оцінка
наближення. Процес ітерації слід
продовжувати до тих пір, доки для двох
послідовних наближений
![]() і
не буде забезпечено виконання нерівності
і
не буде забезпечено виконання нерівності
![]() ,
,
де
- задана похибка кореня
і
![]() .
.
Якщо
![]() ,
то з нерівності
,
то з нерівності
![]() випливає нерівність
випливає нерівність
![]() .
.
Приклад.
Знайти з точністю
![]() один з коренів рівняння
один з коренів рівняння
![]() .
.
Розв’язок.
![]() .
Дане рівняння має корінь на інтервалі
.
Дане рівняння має корінь на інтервалі
![]() .
.
Представимо
рівняння у вигляді
![]() .
У цьому випадку
.
У цьому випадку
![]() .
.
Очевидно,
що при
![]() маємо також
маємо також
![]() .
.
Похідна
![]() .
.
При
маємо
![]() .
.
Умови теореми 1 виконані. Процес ітерації будемо здійснювати до забезпечення виконання нерівності
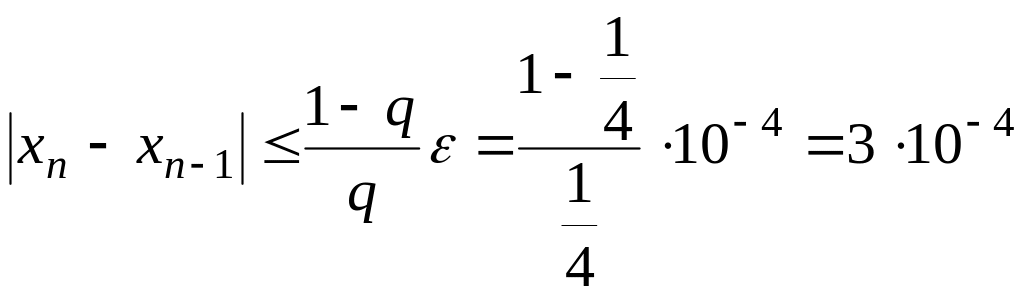 .
.
Покладемо
![]() .
Послідовно обчислюємо:
.
Послідовно обчислюємо:
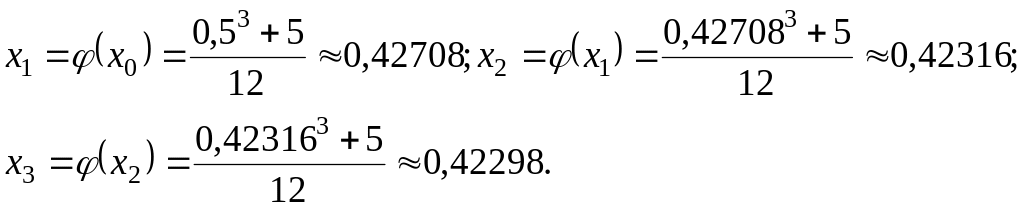
На
цьому процес ітерації можна зупинити,
так як
![]() .
.
Покладемо
![]() .
.
Приклад
2. Знайти методом ітерацій найбільший
додатний корінь рівняння
![]() з точністю
.
з точністю
.
Розв’язок.
Легко впевнитися в тому, що шуканий
корінь
знаходиться на інтервалі
![]() .
Справді,
.
Справді,
![]() і
і
![]() при
при
![]() .
.
Початкове
рівняння можна переписати у вигляді
![]() ,
або
,
або
![]() ,
або
,
або
![]() тощо.
тощо.
Найвигіднішим
серед цих способів є останній, так як,
обравши за основний проміжок
![]() і поклавши
і поклавши
![]() ,
,
знайдемо, що похідна
![]()
за
абсолютною величиною не перевищує
![]() :
:
![]() .
.
Розраховуємо послідовні наближення з одним запасним знаком за формулою
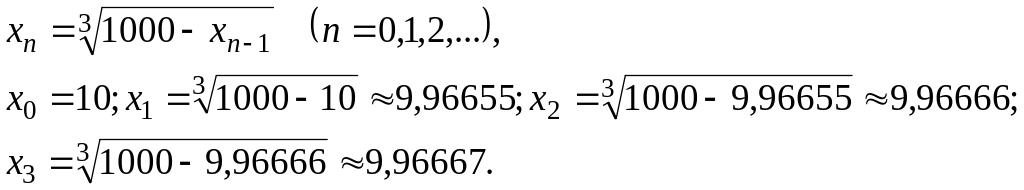
Так
як
![]() ,
то з точністю
,
то з точністю
![]() можна покласти
можна покласти
![]()
Приклад 3. Рівняння
![]()
Має
корінь
![]() ,
так як
,
так як
![]() та
та
![]() .
.
Дане рівняння можна записати у вигляді
![]() .
.
Тут
![]() та
та
![]() ;
;
тому
![]() при
при
![]() .
.
Отже, умови збіжності процесу ітерації не виконуються.
Якщо записати початкове рівняння у вигляді
![]() ,
,
то матимемо
![]() та
та
![]() .
.
Звідси
![]() при
при
![]() ,
отже, процес ітерації є збіжним.
,
отже, процес ітерації є збіжним.
