4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь

Багато задач дослідження різних об’єктів за допомогою моделей приводять до необхідності розв’язування нелінійних рівнянь. Зокрема, досить часто такі задачі виникають при дослідженні пристроїв електронної, радіоелектронної і обчислювальної техніки.

Концепція методів. Методи розв’язування нелінійних рівнянь виду поділяються на прямі і ітераційні.

Прямі методи дозволяють записати розв’язки (корені рівнянь) у вигляді деякого скінченого співвідношення (формули). За допомогою цих методів можна розв’язати тільки деякі найпростіші рівняння (наприклад, квадратні рівняння).

Проте на практиці мають справу з рівняннями більш високого порядку і тому для їх розв’язування використовують ітераційні методи, тобто методи послідовних наближень. Кожний крок уточнення розв’язку називається ітерацією.

Як правило, процес розв’язування нелінійного рівняння виду здійснюється у два етапи:

1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.

2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .

4.1 Відділення коренів

Якщо рівняння досить складне, то його корені порівняно рідко вдається знайти точно. Крім того, в деяких випадках рівняння містить коефіцієнти, відомі лише приблизно, і, отже, сама задача про точне визначення коренів рівняння втрачає сенс. Тому важливе значення мають способи наближеного знаходження коренів рівняння і оцінки ступеня їх точності.

Нехай дано рівняння

(4.1)

де функція визначена і неперервна на деякому скінченому або нескінченному інтервалі .

Надалі в деяких випадках нам знадобиться існування і неперервність першої похідної або навіть другої похідної , що буде обумовлено у відповідних місцях.

Всяке значення , що обертає функцію в нуль, тобто таке, що , називається коренем рівняння (4.1) або нулем функції .

Ми припускатимемо, що рівняння (4.1) має лише ізольовані корені, тобто для кожного кореня рівняння (4.1) існує окіл, що не містить інших коренів цього рівняння.

Для відділення коренів корисною буде відома теорема з математичного аналізу.

Теорема 1. Якщо неперервна функція приймає значення різних знаків на кінцях відрізка , тобто , то всередині цього відрізка міститься щонайменше один корінь рівняння, тобто знайдеться хоча б одне число таке, що (рис. 4.1).

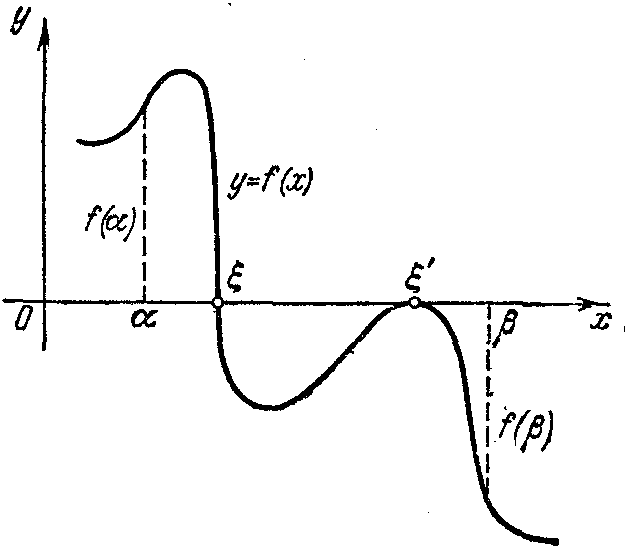
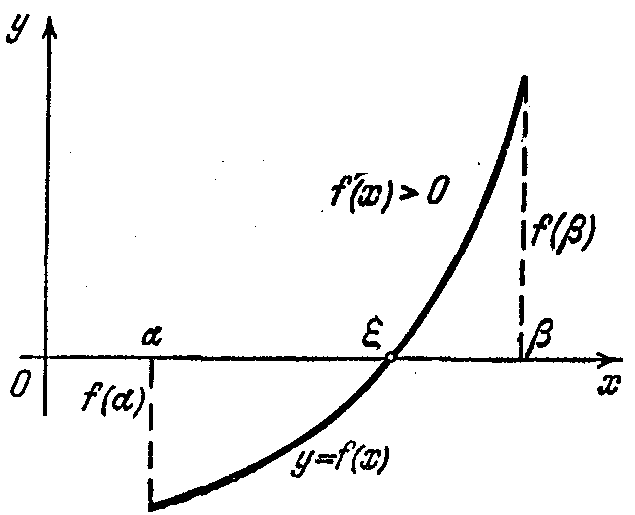
Рис. 4.1 Рис. 4.2

Корінь завідомо буде єдиним, якщо похідна існує та зберігає сталий знак всередині інтервалу , тобто якщо (або ) при (рис. 4.2).

Процес відділення коренів починається з встановлення знаків функції у граничних точках и області її існування.

Потім встановлюються знаки функції у ряді проміжних точок , вибір яких враховує особливості функ­ції . Якщо виявиться, що для деякого матиме місце нерівність , то в силу тео­реми 1 на інтервалі матимемо корінь рівняння . Потім потрібно впевнитися, чи є цей корінь єдиний. Для відділення коренів практично часто буває достатньо здійснити процес половинного поділу, наближено ділячи даний інтервал на дві, чотири, вісім і т. д. рівних частин (до деякого кроку) та визначаючи знаки функції в точках поділу. Корисно пам’ятати, що алгебраїчне рівняння -го степеня

має не більше дійсних коренів. Тому, якщо для такого рівняння ми отримали змін знаків, то всі корені його відділені.

Приклад 1. Відділити корені рівняння

. (4.2)

Розв’язок. Складаємо приблизну схему:

-	-
-3	-
-1	+
0	+
1	-
3	+
+	+

Отже, рівняння (4.2) має три дійсні корені, що лежать в інтервалах .

Якщо існує неперервна похідна і корені рівняння легко обчислюються, то процес відділення коренів рівняння (4.1) можна упорядкувати. Для цього, очевидно, достатньо підрахувати лише знаки функції в точках нулів її похідної і в граничних точках і .

Приклад 2. Відділити корені рівняння

. (4.3)

Розв’язок. Тут , тому при .

Маємо

.

Отже, рівняння (4.3) має тільки два дійсні корені, з яких один лежить в інтервалі , а інший — в інтервалі .

Приклад 3. Визначити число дійсних коренів рівняння

. (4.4)

Розв’язок. Оскільки і , то рівняння (4.4) має тільки один дійсний корінь.

Дамо тепер оцінку похибки наближеного кореня.

Теорема 2 (без доведення). Нехай — точний, а — наближений корені рівняння , що знаходяться на одному і тому ж відрізку , причому при .

У такому разі справедлива оцінка

. (4.5)

Зауваження. Формула (4.5) може дати грубі результати, і її не завжди зручно застосовувати. Тому на практиці тим або іншим способом звужують загальний інтервал , що містить корінь і його наближене значення , і вважають .

Приклад 4. Наближеним коренем рівняння є . Оцінити абсолютну похибку цього кореня.

Розв’язок. Маємо .

Оскільки при одержуємо

,

то точний корінь міститься в інтервалі . Похідна монотонно зростає. Тому її найменшим значенням в даному інтервалі є:

.

Звідси по формулі (4.5) отримаємо:

.