3. Ранг матрицы

3.1. Основные понятия и примеры

Ранг матрицы – это особая числовая функция, заданная на множестве матриц. В отличие от определителя, ранг матрицы существует для матрицы любого порядка.

Прежде чем дать определение ранга матрицы, рассмотрим понятие минора матрицы.

Минором k-го порядка матрицы А называется определитель матрицы, составленной из элементов каких-либо k выделенных строк и каких-либо k выделенных столбцов исходной матрицы А.

Понятие минора k-го порядка широко используется в линейной алгебре. В отличие от минора элемента матрицы, минор k-го порядка не связан с конкретным элементом матрицы и существует для любых, а не только для квадратных матриц. Миноров k-го порядка для любой матрицы может быть много. Например, для матрицы порядка количество миноров k-го порядка определяется числом

.

Главным, или угловым минором k-го порядка матрицы называется минор, составленный из первых k строк и первых k столбцов этой матрицы.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначается как .

Пример 3.1. Пусть , , . Тогда , , .

Любой отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется ее базисным минором.

3.2. Понятия линейной независимости строк и столбцов матрицы. Базис в системе строк (столбцов) матрицы

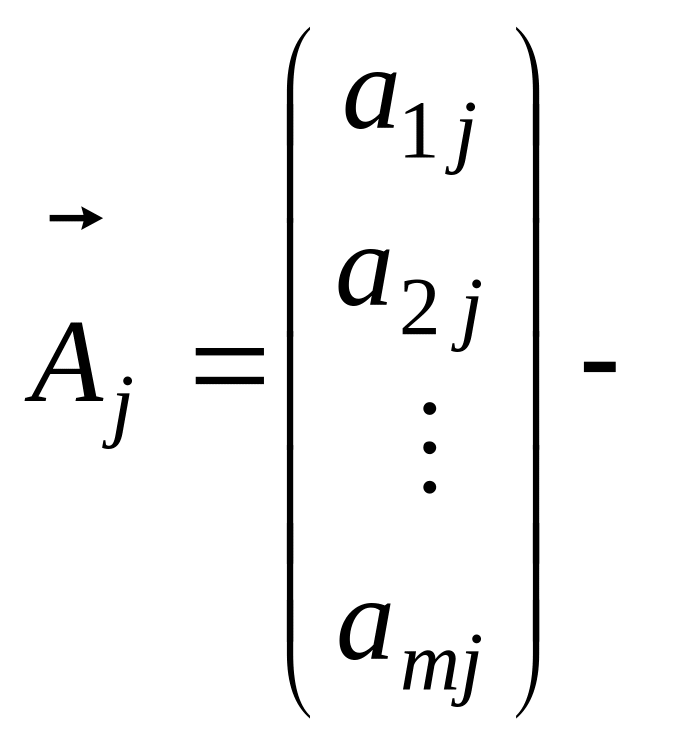Рассмотрим матрицу . Обозначим через j-й столбец матрицы. Система столбцов называется линейно зависимой, а сами столбцы, составляющие систему , линейно зависимыми, если существуют числа , не все равные нулю, такие что

. (3.1)

В противном случае система столбцов называется линейно независимой, а сами столбцы этой системы – линейно независимыми.

Выражение называется линейной комбинацией столбцов .

Система столбцов называется базисом в системе всех столбцов матрицы А, если выполняются следующие условия:

1) все столбцы системы G являются столбцами матрицы А;

2) система G линейно независима;

3) любой столбец матрицы А может быть представлен в виде линейной комбинации столбцов системы G, то есть для каждого существуют такой набор чисел , что .

Аналогично вводятся понятия линейной независимости, линейной зависимости и базиса в системе строк матрицы А.

Пример 3.2. Пусть . Тогда система столбцов , образует базис в системе всех столбцов матрицы A. Действительно:

1) и являются столбцами матрицы A;

2) система этих столбцов линейно независима. Докажем это от противного. Предположим, что существуют такие числа , не равные нулю одновременно, для которых

.

Полученное соотношение эквивалентно системе уравнений

Умножим первое уравнение на и прибавим ко второму. Получим , откуда , что невозможно по предположению.

3) любой столбец матрицы А может быть представлен в виде линейной комбинации столбцов и . Действительно, , .

Ранг матрицы тесно связан с понятием линейной независимости строк и столбцов матрицы.

Теорема о ранге матрицы (о базисном миноре). Ранг матрицы равен числу линейно независимых ее столбцов (строк); при этом система столбцов (строк) матрицы, содержащая базисный минор, образует базис в системе всех столбцов (строк) этой матрицы.

Свойства ранга матрицы

1. .

2. .

3. .

4. .

5. Если А есть диагональная матрица, то равен числу ненулевых элементов ее главной диагонали. В частности, , .

6. Элементарные преобразования матрицы не меняют ее ранга.

7. Для любой матрицы А и любой невырожденной матрицы В справедливо .