
- •Министерство образования и науки рф
- •Национальный исследовательский
- •Томский государственный университет
- •В.И. Рюмкин
- •Матрицы и векторы в экономике
- •1. Матрицы
- •1.1. Определения
- •1.2. Операции над матрицами
- •1.3. Квадратичная форма матрицы. Определенность матрицы
- •1.4. Числовые функции от матриц
- •1.5. Задачи
- •2. Определители
- •2.1. Понятие определителя и его свойства
- •2.2. Алгебраическое дополнение и минор элемента матрицы. Разложение определителей по строке и столбцу
- •2.3. Задачи
- •3. Ранг матрицы
- •3.1. Основные понятия и примеры
- •3.2. Понятия линейной независимости строк и столбцов матрицы. Базис в системе строк (столбцов) матрицы
- •3.3. Методы поиска ранга матрицы
- •3.3.1. Метод окаймляющих миноров
- •3.3.2. Метод элементарных преобразований
- •3.4. Задачи
- •4. Обратная матрица
- •4.1. Основные сведения
- •4.2. Методы поиска обратной матрицы
- •4.2.1. Метод союзной матрицы
- •4.2.2. Метод элементарных преобразований
- •4.3. Задачи
- •5. Векторы
- •5.1. Операции над векторами
- •5.1.1. Алгебраические операции над векторами
- •5.2. Линейная независимость и базис векторов
- •5.3. Геометрическая интерпретация векторов
- •5.3.1. Одномерные, двумерные и трехмерные пространства
- •5.3.2. Многомерные пространства
- •5.4. Задачи
- •6. Линейные преобразования
- •6.1. Основные сведения
- •6.2. Преобразование базиса
- •6.3. Характеристические числа и векторы
- •6.4. Задачи
- •7. Применение векторов и матриц в экономике
- •7.1. Балансовая модель Леонтьева
- •7.2. Модель равновесных цен
- •7.3. Модель международной торговли (модель обмена)
- •7.4. Задачи
- •Литература
- •Оглавление
6.2. Преобразование базиса
Координаты
вектора зависят от выбора базиса. Пусть
вектор в «старом» базисе
имеет координаты
,
а в «новом» базисе
![]() –
координаты
–
координаты
![]() (см. рис.6.1 для случая
(см. рис.6.1 для случая
![]() ).
).
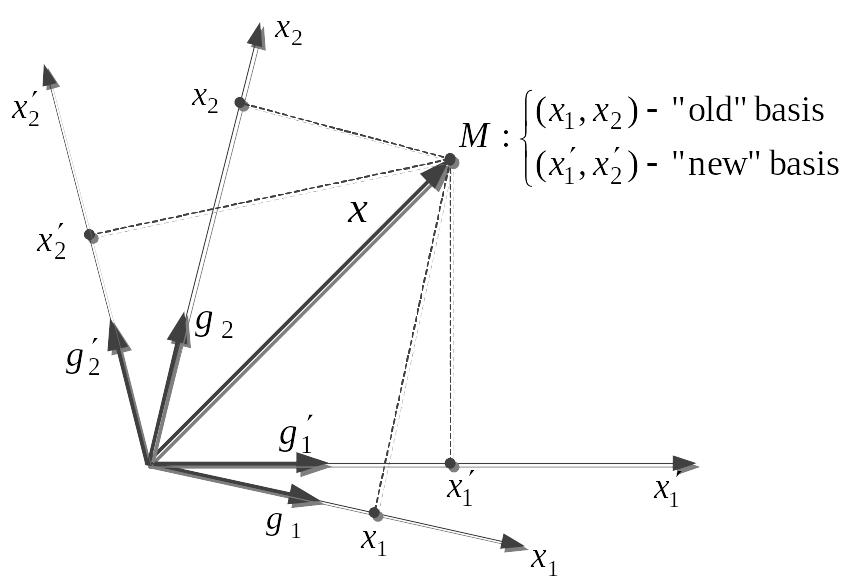
Рис.6.1. Преобразование базиса
Каждый из векторов «нового» базиса можно выразить в виде линейной комбинации векторов «старого» базиса:
![]() 6.4)
6.4)
Полученная
система означает, что переход от «старого»
базиса
к «новому»
задается
матрицей перехода
![]() .
Эта матрица не вырождена, так как в
противном случае ее строки (а, следовательно,
и базисные векторы) оказались бы линейно
зависимыми. Обратный переход от «нового»
базиса
к
«старому» базису
осуществляется с помощью обратной
матрицы
.
.
Эта матрица не вырождена, так как в
противном случае ее строки (а, следовательно,
и базисные векторы) оказались бы линейно
зависимыми. Обратный переход от «нового»
базиса
к
«старому» базису
осуществляется с помощью обратной
матрицы
.
Найдем зависимость между координатами рассматриваемого вектора в «старом» и «новом» базисах. Из формулы (6.1) следует
![]() .
(6.5)
.
(6.5)
Подставляя
выражения
![]() из
системы (6.4) в левую часть равенства
(6.5), после преобразований получим:
из
системы (6.4) в левую часть равенства
(6.5), после преобразований получим:
![]()
то есть, в матричной форме
![]() .
(6.6)
.
(6.6)
Полученные формулы (6.6) представляют собой формулы преобразований координат одного и того же вектора при переходе от «старого» базиса к «новому» базису и наоборот.
Пример
6.1. В базисе
![]() заданы векторы
заданы векторы
![]() ,
,
![]() ,
,
![]() .
Показать, что векторы
образуют базис и выразить в этом базисе
вектор
,
имеющий в базисе
координаты
.
Показать, что векторы
образуют базис и выразить в этом базисе
вектор
,
имеющий в базисе
координаты
![]() .
.
Решение. Векторы образуют базис, если они линейно независимы. Запишем матрицу А, вектор-столбцами которой являются :
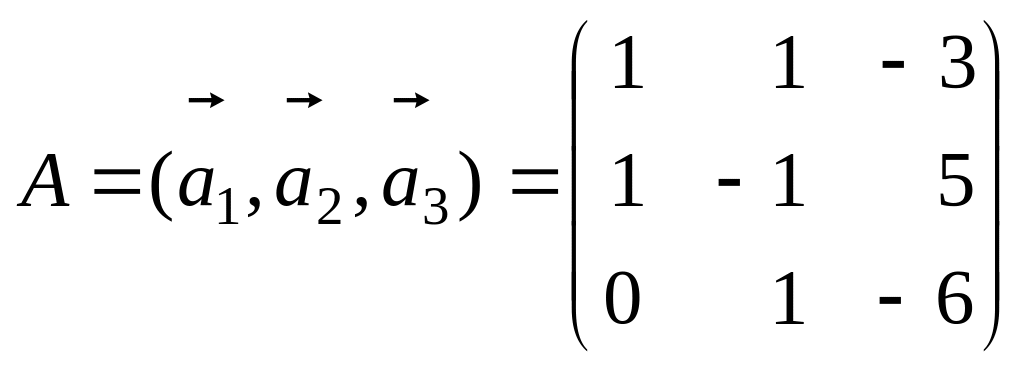 .
.
Нетрудно
показать, что
.
Следовательно,
![]() ,
и система векторов
линейно независима. Связь между базисами
выражается следующим образом:
,
и система векторов
линейно независима. Связь между базисами
выражается следующим образом:
![]()
Матрица
перехода от базиса
к базису
![]() есть
есть
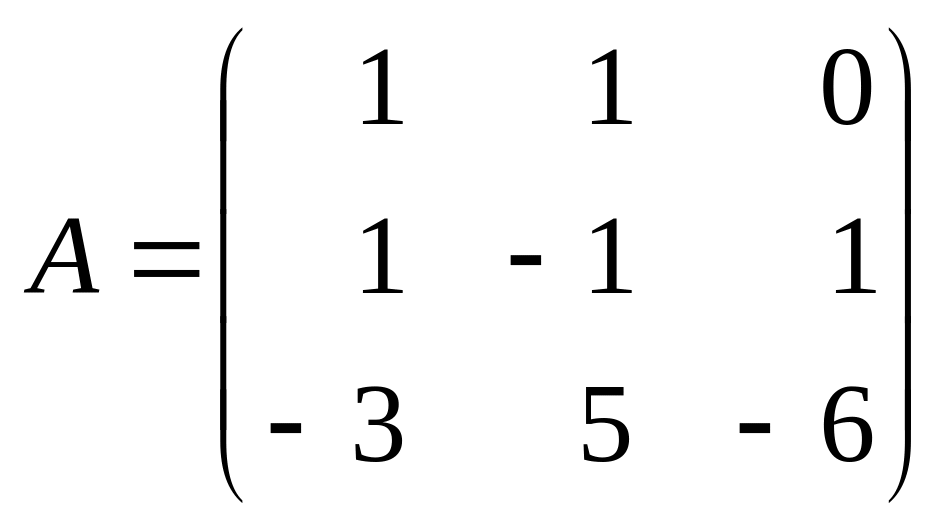 .
Нетрудно показать, что
.
Нетрудно показать, что
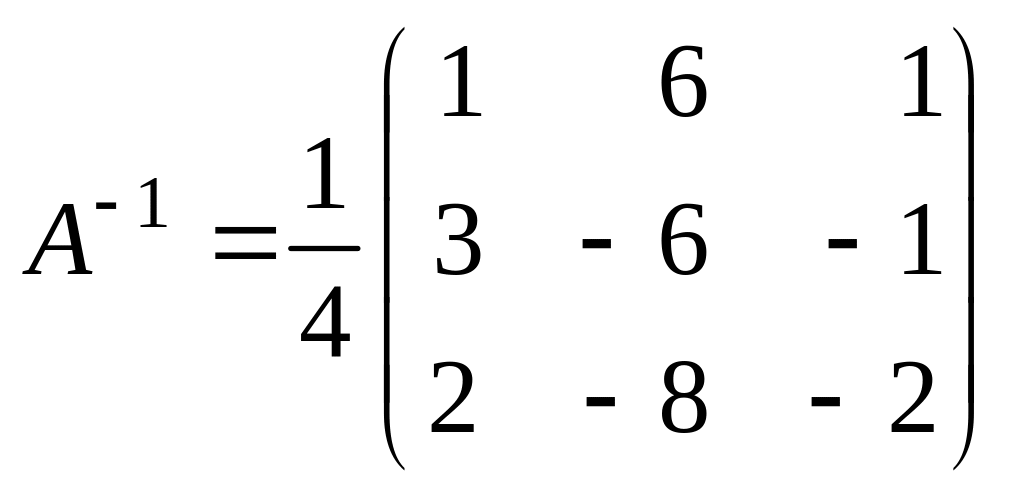 .
Теперь из (6.6) сразу следует
.
Теперь из (6.6) сразу следует
![]()
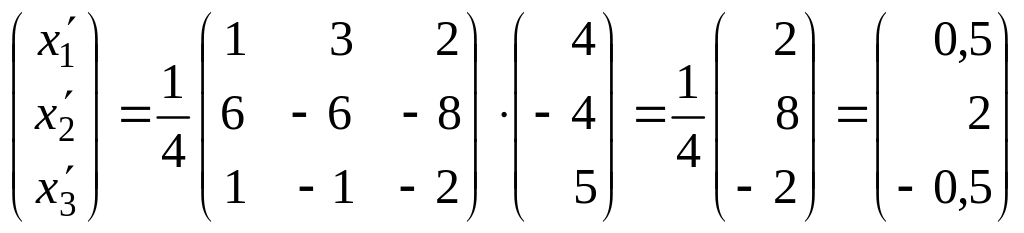 .
.
Таким
образом, новые координаты вектора
в базисе
есть 0,5; 2; –0,5, и вектор
может быть представлен в виде
![]() .
.
6.3. Характеристические числа и векторы
Любое линейное преобразование однозначно определяет матрицу А оператора в заданном базисе пространства .
Ненулевой вектор называется характеристическим (собственным) вектором квадратной матрицы , принадлежащим ее собственному значению , если после преобразования он переходит в вектор, отличающийся от лишь на постоянный множитель , то есть, если
![]() .
(6.7)
.
(6.7)
Числовой множитель называется характеристическим корнем (собственным значением) матрицы А оператора .
Для
любого собственного вектора
матрицы А, принадлежащего
собственному значению
и любого числа
![]() вектор
вектор
![]() также является собственным вектором
матрицы А, принадлежащим собственному
значению
.
также является собственным вектором
матрицы А, принадлежащим собственному
значению
.
Многие прикладные задачи экономики сводятся к проблеме отыскания собственных значений и собственных векторов матриц.
Уравнение (6.7) может быть представлено в виде
![]() . (6.8)
. (6.8)
Матрица
![]() называется
характеристической матрицей.
называется
характеристической матрицей.
Нетривиальное (ненулевое) решение уравнения (6.8) существует лишь в том случае, если определитель характеристической матрицы равен нулю:
![]() . (6.9)
. (6.9)
Уравнение (6.9) называется характеристическим уравнением. Если А – матрица порядка , то характеристическое уравнение является алгебраическим уравнением степени n относительно :
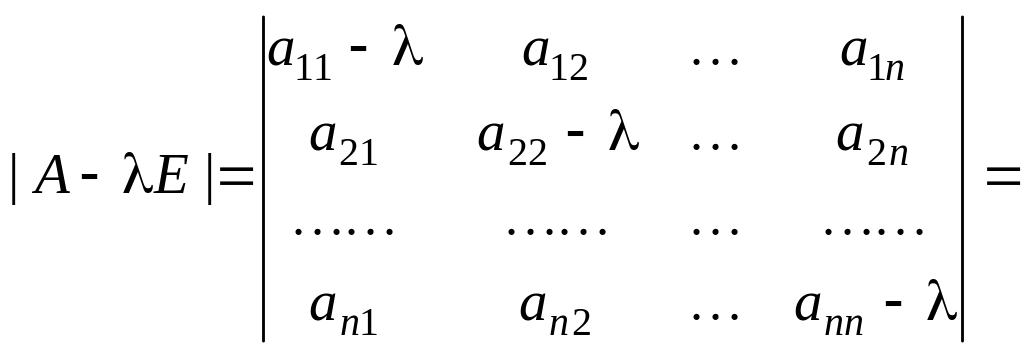
![]() .
.
Это
уравнение имеет n не
обязательно различных корней
![]() причем
некоторые из них могут быть комплексными
числами. Каждому из этих характеристических
корней соответствует характеристический
вектор, определенный с точностью до
постоянного множителя.
причем
некоторые из них могут быть комплексными
числами. Каждому из этих характеристических
корней соответствует характеристический
вектор, определенный с точностью до
постоянного множителя.
Пример
6.2. Характеристическое уравнение для
матрицы
![]() имеет вид
имеет вид
![]() .
Уравнение имеет два корня:
.
Уравнение имеет два корня:
![]() ,
,
![]() .
Характеристическими векторами,
соответствующими
.
Характеристическими векторами,
соответствующими
![]() и
и
![]() ,
являются вектора
,
являются вектора
![]() и
и
![]() ,
где с – произвольная константа.
Произвольные константы часто исключают
из рассмотрения, вводя нормализованные
векторы. В данном примере нормализованными
векторами являются
,
где с – произвольная константа.
Произвольные константы часто исключают
из рассмотрения, вводя нормализованные
векторы. В данном примере нормализованными
векторами являются
![]() и
и
![]() .
.
Свойства характеристических корней
1. Сумма характеристических корней равна следу матрицы:
2.
![]() .
.
3.
Произведение характеристических корней
равно определителю матрицы:![]() .
.
4. Число ненулевых характеристических корней матрицы совпадает с рангом этой матрицы.
5. Характеристическими корнями диагональной матрицы являются элементы ее главной диагонали.
6. Для симметрических матриц все n собственных значений являются вещественными числами.
Согласно теореме Гамильтона-Кэли, матрица А является корнем своего характеристического уравнения:
Теорема Гамильтона-Кэли. Пусть характеристическим уравнением матрицы А является уравнение
.
Тогда справедливо матричное уравнение
![]() .
.
В
некоторых случаях интерес представляет
задача отыскания собственных векторов,
принадлежащих собственному значению
![]() .
Достаточные условия существования
такого собственного вектора вытекает
из следующей теоремы.
.
Достаточные условия существования
такого собственного вектора вытекает
из следующей теоремы.
Теорема о единичном собственном значении. Если в матрице А сумма элементов каждого столбца равна 1, то имеется собственный вектор, принадлежащий собственному числу 1.
Во многих связанных с отысканием собственных векторов прикладных задачах экономики содержательный смысл имеют только собственные вектора с положительными компонентами. Условия существования таких векторов даются теоремой Фробениуса-Перрона.
Теорема Фробениуса-Перрона. Пусть А – неотрицательная квадратная матрица. Тогда:
1.
Максимальное по модулю собственное
значение
![]() матрицы А неотрицательно. Среди
собственных векторов, принадлежащих
имеется неотрицательный вектор.
матрицы А неотрицательно. Среди
собственных векторов, принадлежащих
имеется неотрицательный вектор.
2.
В случае
![]() все неотрицательные собственные векторы
матрицы А положительны и принадлежат
только ее максимальному по модулю
собственному значению
.
Кроме того, в этом случае любые два
положительных собственных вектора
и
отличаются лишь числовым множителем,
то есть,
все неотрицательные собственные векторы
матрицы А положительны и принадлежат
только ее максимальному по модулю
собственному значению
.
Кроме того, в этом случае любые два
положительных собственных вектора
и
отличаются лишь числовым множителем,
то есть,
![]() .
.
