6. Линейные преобразования

6.1. Основные сведения

Если задано правило, по которому каждому вектору ставится в соответствие единственный вектор , то говорят, что задан оператор (преобразование, отображение) , действующий из в (пишут ). Вектор называется образом вектора , а сам вектор – прообразом вектора .

Оператор (преобразование) называется линейным, если для любых векторов и пространства и любого числа k выполняются соотношения:

1. ,

2. .

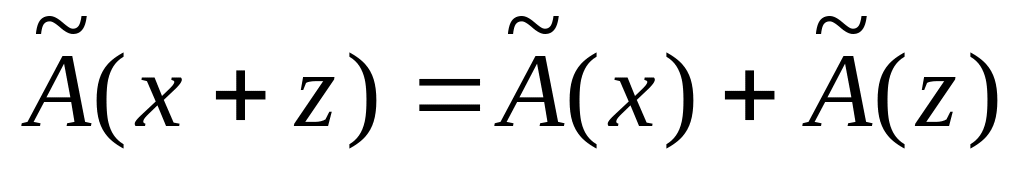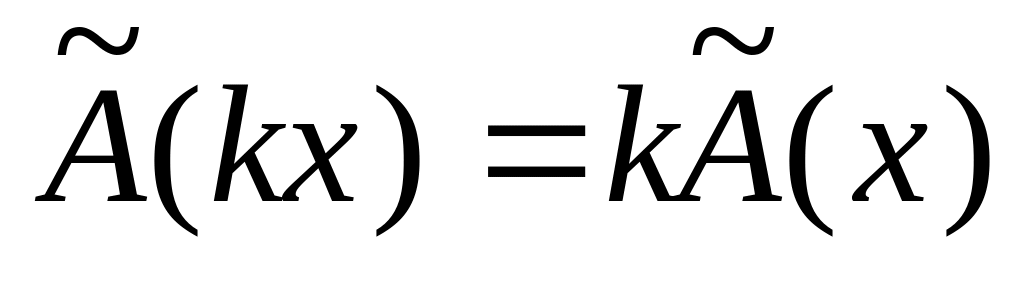Суммой двух линейных операторов и называется оператор , определяемый равенством .

Произведением линейного оператора на число называется оператор , определяемый равенством .

Произведением линейных операторов и называется оператор , определяемый равенством .

Нетрудно убедиться, что операторы , , , полученные в соответствии с определениями, являются линейными.

Определим нулевой оператор , преобразующий все векторы пространства в нулевые векторы пространства : .

Если пространства и совпадают ( ), то оператор отображает в себя. В этом случае можно ввести в рассмотрение тождественный оператор , действующий по правилу .

Покажем, что любому линейному оператору может быть поставлена в соответствие матрица А размера , а закон отображения выразится системой линейных уравнений, связывающих координаты образа и прообраза.

Действительно, пусть система векторов образует базис в пространстве . Тогда любой вектор можно разложить по данному базису:

.

Рассмотрим оператор . В силу линейности оператора образ имеет вид

.

Пусть – базис в пространстве . Поскольку , также является вектором из , то его можно разложить по базису .

Пусть . Тогда

. (6.1)

С другой стороны, вектор , имеющий в том же базисе координаты , можно записать так:

. (6.2)

Вследствие единственности разложения вектора по базису правые части соотношений (6.1) и (6.2) равны, откуда получаем систему линейных уравнений

(6.3)

Матрица , элементами которой являются коэффициенты в системе (6.3), называется матрицей оператора в базисе . Рангом оператора по определению является ранг матрицы А этого оператора в данном базисе.

Таким образом, каждому линейному оператору соответствует матрица в заданном базисе.

Справедливо и обратное: всякой матрице соответствует линейный оператор .

Действительно, для любого вектора существует единственный вектор , который является результатом умножения матрицы А на : .

Данное преобразование является линейным, так как

, ,

где , , а k– скаляр. Отметим, что и что линейное преобразование отображает выпуклое множество из в выпуклое множество, принадлежащее пространству .

Пусть – линейный оператор, действующий в пространстве со скалярным произведением . Линейный оператор называется сопряженным к оператору , если для любых векторов выполняется равенство

.

Для всякого оператора сопряженный оператор существует и единственен.

Если оператор в ортонормированном базисе имеет матрицу , то сопряженный оператор в этом же базисе имеет матрицу , где . Матрица называется сопряженной к матрице и для операторов, действующих в , эта матрица равна транспонированной матрице .