
Сборник задач по высшей математике
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Механико-математический факультет
О.М. Биматова
СБОРНИК ЗАДАЧ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Часть II
Томск
2011
РАССМОТРЕН И УТВЕРЖДЕН методической комиссией ММФ Протокол № 6 от 6 июня 2011 г.
Председатель комиссии
Сборник задач разработан для студентов I курса естественных факультетов. Содержит большое количество задач по основным разделам высшей математики: неопределенный интеграл, определенный интеграл, приложения определенного интеграла к задачам естествознания, ряды, дифференциальные уравнения, функции многих переменных. Для подготовки к тестированию добавлен раздел «Повторение».
2-е издание, переработанное и дополненное
Автор: О.М. Биматова
2
|
ОГЛАВЛЕНИЕ |
|
1. |
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ............................................................ |
4 |
1.1. Понятие неопределенного интеграла и его свойства............................. |
4 |
|
1.2. Замена переменной в неопределенном интеграле ................................. |
6 |
|
1.3. Интегрирование по частям....................................................................... |
8 |
|
1.4. Интегрирование рациональных функций............................................... |
9 |
|
1.5. Интегрирование иррациональных функций......................................... |
12 |
|
1.6. Интегрирование тригонометрических функций.................................. |
13 |
|
2. |
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ............................................................... |
15 |
2.1. Вычисление определенного интеграла................................................. |
15 |
|
2.2. Вычисление площадей плоских фигур ................................................. |
17 |
|
2.3. Вычисление длины дуги плоской кривой............................................. |
21 |
|
2.4. Вычисление объема тела вращения....................................................... |
23 |
|
2.5. Вычисление площади поверхности вращения ..................................... |
25 |
|
3. |
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ.................................................. |
27 |
3.1. Область определения функции многих переменных........................... |
27 |
|
3.2. Частные производные и дифференциалы............................................. |
27 |
|
3.3. Касательная плоскость и нормаль к поверхности................................ |
29 |
|
3.4. Экстремум функции нескольких переменных..................................... |
30 |
|
4. |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ............................................... |
33 |
4.1. Обыкновенные дифференциальные уравнения 1 порядка.................. |
33 |
|
4.2. Линейные дифференциальные уравнения первого порядка............... |
35 |
|
4.3. Однородные дифференциальные уравнения первого порядка........... |
35 |
|
4.4. Дифференциальные уравнения высших порядков, допускающие |
|
|
|
понижение порядка................................................................................ |
36 |
4.5. Комплексные числа ................................................................................ |
37 |
|
4.6. Линейные дифференциальные уравнения высших порядков с |
|
|
|
постоянными коэффициентами............................................................. |
38 |
5. |
РЯДЫ.......................................................................................................... |
41 |
5.1. Признаки сходимости числовых рядов................................................. |
41 |
|
5.2. Степенные ряды...................................................................................... |
45 |
|
6. |
ПОВТОРЕНИЕ........................................................................................... |
48 |
7. |
ОТВЕТЫ ………………………………………………………………… 56 |
|
ЛИТЕРАТУРА ............................................................................................... |
62 |
|
3

1.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1.1.Понятие неопределенного интеграла и его свойства
Опр. 1. Если на промежутке a, b существует такая дифференцируемая функция F(x) , производная которой совпадает с f (x) , то функция F(x) называется первообразной f (x) на
По определению F (x) f (x) .
Опр. 2. Функция F(x) c , определяющая множество всех первообразных для функции f (x) , называется неопределенным интегралом от
функции |
f (x) и обозначается символом f (x) dx . |
|||
По определению f (x) dx F(x) c . |
||||
|
Основные свойства неопределенного интеграла |
|||
|
|
|
d(F(x)) F(x) с. |
|
1. d f (x) dx) f (x)dx . |
2. |
|
||
3.k f (x) dx k f (x) dx .
4.f (x) g(x) dx f (x)dx g(x)dx .
Таблица интегралов
1. |
xndx |
xn 1 |
c, n 1. |
|||||||
|
n 1 |
|||||||||
|
|
|
|
|
|
|
|
|||
3. |
axdx |
a x |
|
c, |
||||||
ln a |
||||||||||
|
|
|
|
|
|
|
|
|||
4. |
sin x dx cos x c . |
|||||||||
6. |
|
dx |
|
ctg x c . |
||||||
sin |
2 |
|
||||||||
|
|
|
x |
|
||||||
2.x 1dx dxx ln x c .exdx ex c .
5. cos x dx sin x c .
7. dx tgx c . cos2 x
4
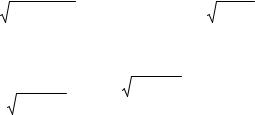
8. |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 arcsin bx |
c , |
|
|
|
dx |
|
|
arcsin x c . |
|||||||||||||
|
|
|
a2 b2 x2 |
|
1 x2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
b |
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
9. |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
|
|
arctg bx c , |
|
|
dx |
arctg x c . |
||||||||||||||||||
|
a |
2 |
2 |
x |
2 |
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
ab |
a |
|
|
|
|
1 x |
|
|
|
|
|
|||||||||||||||||
10. |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
ln |
|
x |
x2 a2 |
|
c . |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x2 a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Вычислить: |
|
|
|
|
|
|
|
2. 3 x 4x2 dx . |
|||||||||||||||||||||||||||||||
1. |
5 x x2 dx . |
|
||||||||||||||||||||||||||||||||||||||
3. |
x3 4x2 1 dx . |
|
4. 6x3 x 1 dx . |
|||||||||||||||||||||||||||||||||||||
5. |
(6x5 |
|
|
4x3 |
2) dx |
|
6. (3x2 |
4x3 5) dx |
||||||||||||||||||||||||||||||||
7. |
|
x 2 |
dx . |
|
|
|
|
|
|
|
|
|
|
8. 3x 6 dx . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
9. |
|
|
2x 2 |
5 dx . |
|
|
|
|
|
|
|
10. |
|
3 2x dx . |
||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
(x2 |
|
|
1)2 |
dx . |
|
|
|
|
|
(x2 2)2 |
|||||||||||||||||||||||||||
11. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
12. |
|
|
|
|
|
|
|
|
dx . |
||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
|
(2 x2 ) |
2 |
|
dx . |
|
|
|
|
|
3 x2 |
||||||||||||||||||||||||||||
13. |
|
|
|
|
|
4x |
|
|
|
|
|
|
|
14. |
|
|
|
|
|
|
dx . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|||||||||
15. |
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
16. |
|
|
|
x |
|
|
dx . |
|||||||||||||||||||
|
|
|
|
x |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
e x |
|||||||||||||||||
17. |
2 |
x |
3 |
|
|
|
|
2 |
|
|
|
18. |
e |
x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x |
|
dx . |
|
1 |
|
|
|
|
dx . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
19. |
tg2 x dx . |
|
|
|
|
|
|
|
|
|
|
20. |
ctg2 x dx . |
|||||||||||||||||||||||||||
5

|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
|
1 x |
2 |
1 x |
2 |
dx . |
22. |
|
1 x |
2 |
1 x |
2 |
dx . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
23. |
|
|
|
dx |
. |
|
|
|
24. |
|
|
dx |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x2 4 |
|
|
|
|
|
|
x2 1 |
|
|
|
||||||||||
25. |
|
|
|
dx |
. |
|
|
26. |
|
|
dx |
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x2 25 |
|
|
4 x2 |
|
|
|
||||||||||||||||
27. |
|
|
dx |
|
|
. |
|
|
|
28. |
|
|
dx |
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|||||||||||||
4x2 9 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
1.2. Замена переменной в неопределенном интеграле |
|||||||||||||||||||||
|
Пусть f (x) |
– непрерывная функция на промежутке a, b . Чтобы в |
||||||||||||||||||||||
интеграле f (x) dx сделать замену переменной x g(t) , нужно:
1)в выражении подынтегральной функции x заменить на g( f ) ;
2)dx заменить на g (t)dt ;
3)вычислить полученный интеграл;
4)в первообразной функции заменить t его выражением через x .
|
Вычислить: |
|
|||||
29. |
sin |
x |
dx . |
|
|||
|
|
|
|||||
|
2 |
|
|
|
|
||
|
|
x |
|
|
|||
31. |
cos |
|
|
4 |
dx . |
||
2 |
|||||||
|
|
|
|
|
|||
33. (3 2x)4 dx .
dx
35. (2x 5)2 .
5dx
37.x 4 .
30. |
sin 3x dx . |
|
|||||||
32. |
|
|
|
|
|
|
|
|
|
cos |
3 |
x dx . |
|||||||
|
|
|
|
|
|
|
|||
34. |
(6x 1)5 dx . |
||||||||
36. |
|
dx |
|
|
|
. |
|
||
(3x 8) |
3 |
|
|||||||
|
|
|
|
|
|||||
38. |
|
dx |
|
. |
|
|
|
|
|
2x |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
6
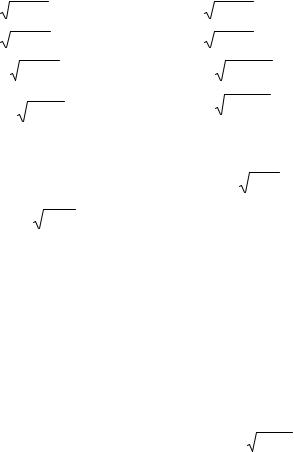
39. |
|
4dx |
|
|
|
|
|
|
|
|
|
|
|||
1 3x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
41. |
|
3x 5 dx . |
|
|
|||||||||||
43. |
|
|
6 2x dx |
|
|
||||||||||
45. |
x |
x2 |
|
3 dx . |
|||||||||||
47. |
3x |
|
x2 1 dx . |
||||||||||||
49. |
cos3 xsin x dx . |
||||||||||||||
51. |
cos xsin 2 x dx . |
||||||||||||||
53. |
sin x |
|
|
cos x dx . |
|||||||||||
55. |
|
|
|
|
dx |
|
|
|
|
. |
|
||||
tg x cos |
2 |
x |
|
||||||||||||
|
|
|
|
|
|||||||||||
57. |
tg x dx . |
|
|
|
|
|
|
||||||||
59. |
ctg |
x |
dx . |
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
61. |
|
1 2cos x |
dx . |
||||||||||||
|
sin |
2 |
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
4 x |
|
|||
63. |
|
|
|
|
|
|
e |
|
|
dx |
|||||
|
x |
2 |
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
65. |
e x ex dx . |
||||||||||||||
67. |
|
|
3x |
|
|
3 |
|
|
|
||||||
e |
|
x |
dx . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
69. |
cos x esin x dx . |
||||||||||||||
40. |
|
|
2dx |
|
|
|
|
|
|
|
|
|
|
|||||
4 3x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
42. |
|
6x 4dx . |
|
|
|
|||||||||||||
44. |
|
|
6 5x dx |
|
|
|
||||||||||||
46. |
x |
|
|
|
4x2 1 dx . |
|||||||||||||
48. |
|
x |
|
|
|
1 2x2 |
|
dx . |
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
50. |
cos2 x sin x dx . |
|||||||||||||||||
52. |
cos x |
|
|
|
sin x dx . |
|||||||||||||
54. |
|
|
tg |
x |
|
|
|
dx . |
|
|
|
|
|
|||||
cos |
2 |
x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
56. |
|
ctg x |
|
dx . |
|
|
|
|
|
|
||||||||
sin |
2 |
x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
58. |
ctg x dx . |
|
|
|
|
|
|
|||||||||||
60. |
tg (3x) dx . |
|
|
|
|
|
|
|||||||||||
62. |
|
2 |
3sin x |
dx . |
|
|||||||||||||
|
cos |
2 |
|
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
5 x |
|
|
|
5 |
|
|
|
|||||||
64. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
e |
|
|
|
|
|
1 x |
2 |
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
66. |
ex |
|
e x 2 dx . |
|||||||||||||||
|
|
|
4 |
|
|
e 4x |
|
|
|
|
|
|||||||
68. |
|
|
|
|
|
|
dx . |
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
70. |
cos x e3sin x dx . |
|||||||||||||||||
7
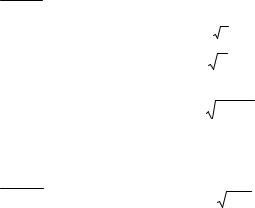
etg x
71. cos2 x dx .
73. x4ex5 dx .
75. x e x2 dx .
77. lnxx dx .
dx
79. xln2 x .
|
|
|
e |
ctg x |
|
|
dx . |
||||
72. |
|
|
|
|
|
|
|
||||
2sin |
2 |
x |
|||||||||
|
|
|
|
|
|||||||
74. |
|
e |
|
x |
|
dx . |
|
||||
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
||||
76. |
|
|
|
ex |
|
|
dx . |
||||
|
5 ex |
||||||||||
|
|
|
|
||||||||
78. |
|
|
dx |
|
|
. |
|
|
|||
x ln x |
|
|
|||||||||
|
|
|
|
|
|||||||
80. |
|
|
|
dx |
|
. |
|||||
x |
ln x |
||||||||||
|
|
|
|||||||||
1.3. Интегрирование по частям
Пусть u(x) и v(x) – непрерывно дифференцируемые на промежуткеa, b функции, тогда
u(x) dv(x) u(x) v(x) v(x) du(x) .
Формулу интегрирования по частям применяют, если интеграл справа проще, чем исходный интеграл слева. Пусть под знаком интеграла слева
стоит произведение многочлена на sin x , или на cos x , или на ex . Тогда за функцию u(x) следует взять многочлен. Пусть под знаком инте-
грала слева стоит произведение многочлена на трансцендентную функцию ( ln x , arctgx , arcsin x , …). Тогда за функцию u(x) следует взять
трансцендентную функцию.
|
Вычислить: |
|
|
81. |
2xsin x dx . |
82. |
(x 1)sin x dx . |
83. |
(x 1)sin x dx . |
84. |
(3x 1)cos x dx . |
85. |
(x2 2x)cos x dx . |
86. |
(x x2 )cos x dx . |
8

87. |
(5 x2 )sin x dx . |
88. |
(6 x2 )sin x dx . |
||
89. |
x exdx . |
90. |
(2 x)exdx . |
||
91. |
(6 x2 )exdx . |
92. |
(x x2 ) exdx . |
||
93. |
x ln x dx . |
94. |
ln x dx . |
||
95. |
6x ln (3x) dx . |
96. |
4x ln 4x dx . |
||
97. |
(x 1) ln2 x dx . |
98. |
(2x 3)ln2 x dx . |
||
99. |
(x2 2x 1) ln2 x dx . |
100. |
(3x2 2x) ln2 x dx . |
||
101. |
x arctg x dx . |
102. |
arcsin x dx . |
||
103. |
x ln x dx . |
104. |
arctg x dx . |
||
1.4. Интегрирование рациональных функций
Рациональной функцией или рациональной дробью называется отно-
шение двух многочленов: f (x) P(x) .
Q(x)
В основу интегрирования рациональных функций положено разложение ее на простые дроби и интегрирование их. Простыми называются дроби следующих четырех типов:
I. |
|
A |
|
, |
|
|
|
|
|
|
|
II. |
A |
|
, m 1 и целое, |
|
|
|
|
|
|
|
|
|
|
|
|
(x b)m |
|||||
x b |
|
|
|
|
|
|
||||||||||
III. |
Mx N |
, |
|
|
|
IV. |
|
Mx N |
, D p2 4q 0 . |
|||||||
x2 |
px q |
|
|
|
(x2 |
px q)m |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
Интегрирование простых дробей: |
|
|
|
|||||||||||
I. |
|
|
|
Adx |
Aln |
|
x b |
|
c , |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
x b |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9

II. |
|
|
Adx |
|
|
|
|
|
A |
|
|
|
|
|
|
|
c , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
(m 1)(x b) |
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(x b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
III. |
(Mx N )dx |
|
M ln (x2 |
px q) |
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
px q |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Mp |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
p |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
N |
2 |
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
c . |
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
q |
|
p |
|
|
|
|
|
|
|
|
q |
p |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Вычислить интеграл |
|
|
2x3 x2 x 2 |
dx . |
|||||||||||||||||||||||||
|
|
(x 1) |
2 |
(x |
2 |
x |
1) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как степень числителя |
|
P(x) 2x3 |
x2 x 2 меньше, чем |
||||||||||||||||||||||||||
степень знаменателя |
Q(x) (x 1)2 (x2 |
|
x 1) , |
|
|
то под знаком инте- |
|||||||||||||||||||||||
грала стоит правильная рациональная дробь. Разложим ее на сумму простых дробей с неопределенными пока коэффициентами в числителях:
2x3 x2 x 2 |
|
A |
|
|
|
A |
|
Mx N |
|
|
||
|
|
|
1 |
|
|
|
2 |
|
|
|
. |
|
(x 1)2 (x2 |
x 1) |
x |
1 |
(x 1)2 |
x2 x |
1 |
||||||
|
|
|
|
|||||||||
Приведем к общему знаменателю сумму в правой части равенства и приравняем числители левой и правой части равенства:
2x3 x2 x 2 A1(x 1)(x2 x 1) A2 (x2 x 1) (Mx N)(x 1)2 .
Теперь приравняем коэффициенты при одинаковых степенях x :
3 : 2 A1 M
2 : 1 A2 N 2M
1: 1 A2 M 2N
0 : 2 A1 A2 N
Решение системы: A1 1, A2 2 , N 1, M 1. Таким образом
10
