Сборник задач по высшей математике

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

c2 x3 cn 1 b xn x

.pdf

Скачиваний:

Добавлен:

30.05.2015

Размер:

457.05 Кб

Скачать

☆

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

2x3

x2 x 2

1) dx

(x 1)

x 1)

x 1

(x 1)

x 1

1 ln(x2

x 1)

arctg 2x 1 c .

x 1

Вычислить интегралы:

2dx

105.x 2 .

107. 2 x .

109. (x 3)5 .

111. (2x 1)7 .

(3x 2) dx

113. x2 4x 5 .

(x 5) dx

115. x2 2x 2 .

(3 x) dx

117. x2 2x 2 .

(2 x) dx

119. x2 6x 10 .

(x 4) dx 121. (x 2)(x 3) .

123. x(x 5) .

(2x 1) dx 125. (x 1)(x 2) .

3dx

106.x 3 .

5dx

108.x 2 .

110.			dx		.
110.	(3x 6)			5	.
	(3x 6)
112.			dx		.
112.	(3x 1)4				.
	(3x 1)4
114.	(3x 2) dx						.
114.	x	2	4x 5				.
	x		4x 5
116.	(5x 2) dx						.
116.	x	2	2x 2				.
	x		2x 2
118.	(2x 1) dx							.
118.	2							.
	x 2x 2
120.	(2x 5) dx								.
120.	x	2	6x 10						.
	x		6x 10
122.		(2x 7) dx
122.	(x 1)(x 2)
	(x 1)(x 2)
124.			dx
124.	(x		3)(x 4)
	(x		3)(x 4)
126.	(3x 2) dx					.
126.	2					.
	2x		x 3

127.	(x 3) dx										.
127.	2										.
	x	6x 7
129.	3x2 2x 3											dx .
129.		x	3	x								dx .
		x		x
131.			(2x 5) dx												.
131.	(x 2)(x 3)(x													4)	.
	(x 2)(x 3)(x													4)
133.	(2x2 7x 3) dx													.
133.	(x 1)						2	(x 2)						.
	(x 1)							(x 2)
135.				dx									.
135.	(x		3)(x					2				2)	.
	(x		3)(x									2)
137.	(x	2) dx								.
137.	3	2								.
	x	2x
139.	(x3	2x2 4x 2)dx														.
139.							x		2			1				.
	x3						x					1
141.	x3	dx				.
141.						.
	x 2
143.	x4 dx				.
143.	2				.
	x	2

128.	(x 5) dx										.
128.	2										.
	x	x 12
130.	(2x 1) dx										.
130.	x	3	4x								.
	x		4x
132.			12x dx												.
132.	(x 1)(x 2)(x													8)	.
	(x 1)(x 2)(x													8)
134.	(x2 8x 2) dx												.
134.	(x	1)			2	(x					2)		.
	(x	1)				(x					2)
136.			dx									.
136.	(x		2)(x				2				4)	.
	(x		2)(x								4)
138.	(3x 8) dx									.
138.	3 2									.
	x	4x
140.	(x3	4x2 9x 4) dx														.
140.						x		2			1					.
						x					1
142.	(x 1)3 dx
									.
	x2		x						.
144.	x4 dx			.
144.	2			.
	x	3

1.5. Интегрирование иррациональных функций

Пусть R(x, y)	– рациональная функция переменных x и y . Рас-
			ax b
смотрим интеграл		n

	R x,			dx . Этот интеграл приводится к
			px q

интегралу от рациональной функции с помощью подстановки

t n ax b . px q

Если подынтегральная функция рационально зависит от нескольких кор-

нейсодинаковымиподкореннымивыражениями R n ax b, всекорнинужноприводитькодномупоказателю.

145.		dx		.						146.					dx			.
		1	x											x	3 x

147.	x		x 1 dx .							148.			x		3x 1				dx .
															5
		x 1
149.						dx .				150.					x dx							.
		3 3x 1												2x 1						1

151.		x 1				dx .				152.					dx							.
		2x 1										3		3x 1						1

153.		x dx			.					154.				x			dx .
											3			a	x

		x 1
155.		x 1					dx .			156.					x3 dx						.
		x x		2									3 x
															2 1 1
157.			x dx										3 3 x 4 x 3
									.	158.
		x 1 3 x 1
															5 x 3
159.			x dx											x dx
								.		160.						.
		(3x 1)					3x 1
													1 3 x

m ax b , то

dx .

1.6. Интегрирование тригонометрических функций

Интегралы от квадратов и других четных степеней синуса и косинуса находят, применяя формулу понижения степени:

sin2 x	1 cos 2x	, cos2	x	1 cos 2x	, sin xcos x sin 2x .
	2			2	2

Интегралы от кубов и других нечетных степеней синуса и косинуса находят, отделяя от нечетной степени один множитель и полагая кофункцию равной новой переменной.

Интеграл cosm xsin n x dx находят по первому правилу, если m и

n – четные, и по второму правилу, если m или n – нечетные.
Интеграл							R(sin x,cos x) dx										сводят к интегралу от рациональной
функции с помощью подстановки:																													2
				tg		x	t ,				dx			2dt		, sin x				2t			, cos x			1 t			2	.
				tg		2	t ,				dx		1		t 2	, sin x		1 t 2					, cos x			1		t	2	.
						2							1		t 2			1 t 2								1		t	2
161.	sin 2 x dx .																162.	sin 2 (3x) dx .
	cos				2	x												cos				2	x
163.								dx .									164.								dx .
163.								dx .									164.								dx .
						2																	4
165.	sin xcos x dx .																166.	sin 2x cos 2x dx .
167 sin 3x cos3x dx .																	168.	sin 5x cos5x dx .
169.	sin x cos6 x dx .																170.	cos x sin 4 x dx .
171.	(1 sin 2x)2 dx .																172.	(1 2cos x)2 dx .
173.	sin2					x cos3 x dx .											174.	sin3 x cos3 x dx .
175.	sin 2 x cos x dx .																176.	cos2 xsin x dx .
177.	sin3 x cos x dx .																178.	cos3 xsin x dx .
179.						cos x						dx .					180.					1 cos x						dx .
179.		1		cos x sin x								dx .					180.		1		cos x sin x							dx .
		1		cos x sin x															1		cos x sin x
181.				dx					.								182.							dx			.
																				sin x(1 sin x)
			sin x 1																	sin x(1 sin x)
183.				dx						.							184.				5dx				.
183.		1		cos x						.							184.		1		sin x				.
		1		cos x															1		sin x

2.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

2.1.Вычисление определенного интеграла

Пусть функция f (x) определена и ограничена на замкнутом промежутке a,b . Разобьем a,b произвольным образом на n частей точка-

ми	a x0 x1 x2 ... xn 1	xn b . Разности	x0 x1 x0 ,
x1	x2 x1 , x2 x3 x2 , …,	xn 1 xn xn 1 дадут длины час-

тичных промежутков, наибольшую из длин обозначим . На каждом из частичных промежутков возьмем по точке и обозначим их буквами c0 ,

c1 , c2 , … , cn 1 .

Опр. 3. Сумма

f (c0 ) x0 f (c1) x1 f (c2 ) x2 ...

n 1

f (cn 1) xn 1 f (ci ) xi

называется интегральной суммой для функции f (x) по промежутку

a,b . Геометрически интегральная сумма дает площадь ступенчатой фигуры, изображенной на рис. 1.

Рис. 1

Опр. 4. Если при 0 существует предел интегральных сумм , то этот предел называется определенным интегралом от функции f (x)

по промежутку a,b и обозначается символом

f (x) dx .

Формула Ньютона–Лейбница: a

f (x) dx F(b) F(a) .

То есть определенный интеграл равен разности значений первообразной функции на верхнем и нижнем пределах.

Вычислить интегралы по определению, разбивая отрезок a,b на равные части и выбирая за точки ci левые или правые концы отрезков разбиения.

	10		b
185.	ex dx .	186.	ex dx .
	1		a
	4		10
187.	x2 dx .	188.	x2 dx .
	0		5
	10		1
189.	(x 5) dx .	190.	x3 dx .
	0		0
	1		1
191.	(x3 1) dx .	192.	(x	3	2) dx .
	0		0

Вычислить интегралы по формуле Ньютона–Лейбница:

	3		dx				4		dx
195. 0			dx			196. 0			dx				.
				.
		x2 9		.				x2 16
	2						1			2
			x dx			198.			x	2	dx
197.			x dx		.				x		dx			.
197.					.									.
	0		x4 1				0		x6 4
	1						0		x dx
199.			x dx .			200.	0					4 .
199.			x dx .			200.						4 .
	2
									4 x
	0		1 x4				1		4 x
			2.2. Вычисление площадей плоских фигур
Пусть фигура ограничена кривыми							y f (x) ,								y (x) ,	f (x) (x)
и вертикальными прямыми x a ,						x b .

y f (x)

y (x)

a	b	x
	Рис. 2

Площадь фигуры равна определенному интегралу от разности функ-

ций, ограничивающих фигуру: S f (x) (x) dx .

Пусть фигура ограничена кривой, заданной в параметрической форме:

x (t)	, t T	,T и осью ОХ.
	1	2
y (t)

Площадь фигуры равна определенному интегралу:

S (t) (t) dt .

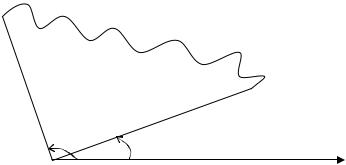
Пусть фигура ограничена двумя лучами , и кривой, заданной в полярной системе координат: r r( ) .

r r( )

Рис. 3

Площадь такой фигуры: S 1 r2 ( ) d .


Вычислить площадь фигур, ограниченных кривыми:
201.	y 4 x2 ,		y 0 .		202.	y 9 x2 , y 0 .
203.	y 8 x2 ,		y 0 .		204.	y 16 x2 , y 0 .
205.	y 4x 3 x2 ,			y 0 .	206.	y 3 2x x2 ,			y 0 .
207.	y 4x 5 x2 ,			y 0 .	208.	y 12 4x x2 ,			y 0 .
209.	y x2	7x, y 30 .			210.	y x2	5x, y 6 .
211.	y x2	2x, y 8			212.	y x2	x, y 12
213.	y2 x , x 25 .				214.	y2 4x ,		x 9 .
215.	4 y2 x , x 9 .				216.	9 y2 x ,		x 4 .

217.	y2 x 1, x 3 .		218.	y2	x 4 , x 0 .
219.	y2 2x 1 , x 4 .		220.	y2	x 3 , x 1.
221.	y 2x2	8x, y x 5	222.	y 2x2 4x, y x 5
223.	y 2x2	6x 8, y x 2	224.		y x2 4x, y x 4

225.xy 4 , x 1, x 4 , y 0 .

226.xy 6 , x y 7 0 .

227.xy 5 , x 5 , x 10 , y 0 .

228.xy 3, x 3 , x 1, y 0 .

229.	y x2 , y 2 x2 .												230.	4 y x2 , y x2								3 .
231.	y ln x ,						x			1	,	y 0 .	232.		y x3 ,					y x .
										e											1
233.	y ln x ,						x e ,					y 0 .	234.		y ln x , x						1	,		y 0 .
233.	y ln x ,						x e ,					y 0 .	234.		y ln x , x						e2	,		y 0 .
	y2 1 x, y x 5														y2						e2
235.	y2 1 x, y x 5												236.		y2		12 3x, y x 2
	x 6cost														x	2		y	2	1.
237.									.				238.		x			y
237.									.				238.	9
	y sin t													9			4
	x t sin t																						3	t
239.	x t sin t									,	t 0, 2 и ось ОХ.									x cos				t	.
239.		y	1 cost							,	t 0, 2 и ось ОХ.						240.						3		.
		y	1 cost																				3	t
																				y sin				t
					2
	x t										, t [ 3, 0] и ось абсцисс.
241.				t			2				, t [ 3, 0] и ось абсцисс.
	y					(t		3)
	y		3			(t		3)
			3
					3
	x t
242.			3						, t [0, 2 2] и оси координат.
242.			3				t 2		, t [0, 2 2] и оси координат.
							t 2
	y		4
	y		4				2
							2

	x t 2
243.		t3			,
243.		t3	t		,
	y	4	t
		4
	x t3
244.				t 4	,
244.		4		t 4	,
	y	4		4
				4

t 2,0 и ось абсцисс.

t 0, 2 и оси координат.

Нарисовать на плоскости множество точек, координаты которых удовлетворяют уравнению в полярной системе координат:


245. r = 2					246. r – 3 = 0
247. r – 1 = 0					248. r = 4
249.					250.
		4
251.	2				252.		7
							6
253.	600				254.	= 1350
В полярной системе координат (r, ) построить точки:
255.	А (3, 0)				256.	В (2,			)
								4
257.	А (2,		5	)	258.	В (1,			)

							2
	3

Найтиполярныекоординатыточек, заданныхвдекартовойсистеме:

259.	A(3, 3)	260.	B( 3, 3)
261.	A( 4, 4)	262.	B(2, 2)
263.	A( 1, 3)	264.	B( 2, 2)

Преобразовать к полярным координатам уравнения линий:


265.	x2	y2			1						266.	x2 y2 4
267.	x2	y2			2x						268.	(x2 y2 )2 9(x2									y2 )
Вычислить площадь фигуры, ограниченной кривой:
269.	r			, [0,				]			270.	r , [				,		3		]
269.	r		2	, [0,			3	]			270.	r , [			4	,		4		]
			2
271.	r					, [ ,			3	]	272.	r		, [			4		,			5	]
271.	r				4	, [ ,			2	]	272.	r	3	, [			3		,			3	]
273.	r 3 sin										274.	r 2 sin
275.	r 2(1 cos ) .										276.	r 3(1 cos ) .

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20193.73 Mб5РЮМКИН_МАТРИЦЫ_И_ВЕКТОРЫ.doc
#
23.11.201986.53 Кб3с 9 по 13 вопросы.doc
#
30.05.201540.8 Mб47С.Реминный - Тайны кофе разных стран.pdf
#
30.05.201514.87 Mб38Самарский Численные методы.pdf
#
08.05.2019109.57 Кб27Сафронов_пс айкидо.doc
#
30.05.2015457.05 Кб45Сборник задач по высшей математике.pdf
#
23.11.2019337.92 Кб35сборник задач по ПОПД перед2.doc
#
30.05.20151.99 Mб39Сборник статей. Тараканова.pdf
#
30.05.2015701.41 Кб6Сборник-23-х-чтений.docx
#
26.03.20165.6 Mб204СБУ т-3 ред.doc
#
29.04.2019108.54 Кб7Сваровская А. С..doc