Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Сборник задач по высшей математике

.pdf

Скачиваний:

Добавлен:

30.05.2015

Размер:

457.05 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Достаточное условие экстремума функции. Пусть в некоторой окрестности точки (x0 , y0 ) функция F(x, y) имеет непрерывные частные

производные второго порядка. Если в критической точке (x0 , y0 ) ее вторые частные производные удовлетворяют условиям:

(x0 , y0 ) 0

(x0 , y0 )

(x0

, y0 )

x y

2 F

(x0 , y0 )

(x0

, y0 )

y x

то функция F(x, y)

имеет минимум в точке (x0 , y0 ) ;

(x0 , y0 ) 0

если

(x0

, y0 )

(x0

, y0 )

x y

2 F

(x0

, y0 )

(x0

, y0 )

y x

то функция F(x, y)

имеет максимум в точке (x0 , y0 ) .

Если определитель второго порядка меньше 0, то функция не имеет экстремума в точке (x0 , y0 ) .

Еслиопределительравеннулю, то нужныдополнительные исследования. Найти экстремумы функции:

401.z x4 y4 x2 2xy y2 .

402.z x2 xy y2 9x 6 y 20 .

403.z e2 (x y2 ) .

404.z sin x sin y sin(x y) , 0 x 2 , 0 y 2 .

405.z xy 50x 20y .

406.z x2 xy y2 4x y 6 .

407.z y x y2 x 6 y .

408.z 3x 6 y x2 xy y2 .

409.z x3 8y3 6xy 1.

410.z 2xy 4x 2 y .

Найтинаибольшееинаименьшеезначенияфункциивзаданнойобласти:

411.z 3x2 7xy y2 5, x2 y2 4 .

412.z 2x2 xy 2 y2 3x 2 y 2 , в замкнутом треугольни-

ке с вершинами в точках (0,0), (0,2), (2,0).

413.В сферу радиуса R вписать прямоугольный параллелепипед наибольшего объема.

414.В треугольнике с вершинами А(2,1), В(5,2), С(3,4) найти точку, сумма квадратов расстояний от которой до вершин была бы наименьшей.

Найти экстремумы функций:

415.z x y , при условии x12 y12 a12 .

416.z x y , при условии x12 y12 12 .

417.z xy , при условии x2 y2 1.

418.z xy , при условии x2 y2 2 .

419.z x 2 y , при условии x2 y2 5 .

420.z 6 5x 4 y , при условии x2 y2 9 .

421.z 3 x 4 y , при условии y2 2x2 1.

422.z x2 y2 , при условии ax by 1.

4.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

4.1.Обыкновенные дифференциальные уравнения 1-го порядка

Опр. 9. Уравнение, содержащее независимые переменные, неизвестную функцию и производные от нее, называется дифференциальным уравнением (ДУ).

Опр. 10. ДУ называется обыкновенным, если неизвестная функция зависит от одной независимой переменной.

Опр. 11. Максимальный порядок входящей в уравнение производной неизвестной функции называется порядком ДУ.

Общий вид ДУ первого порядка имеет вид:

F(x, y, y') 0

(1)

Опр. 12. Решением ДУ называется любая функция y (x) , которая при подстановке ее в уравнение обращает его в тождество.

Опр. 13. Общим решением ДУ (1) называется функция y (x, c) ,

зависящая от одной произвольной постоянной c , и любое решение (1) получается из общего, если произвольной постоянной c придать конкретное значение.

Опр. 14. Уравнением с разделяющимися переменными называется обыкновенное ДУ первого порядка вида:

		M (x) N( y) y' A(x) B( y) .				(2)
Определить порядок ДУ:
423.	y' y'' x3		424.	y''' x5	y4
425.	3y' 10 y2	1	426.	y4 x5	y''
427.	3 y' y3	1	428.	3y''	y' 1
Укажите ДУ первого порядка:			– y'tgx 1
429.	y x x2	1	– y'tgx 1
	(1 ex )dx e y dy		(2 y')2 x y3
430.	x y 1 y		( y')3 3 x
	xdy ydx		y'' 3y' 1
						33

431.	x y' x4 1 0		( y')4 x 1
	y2 dy 5x3dx 0		y'' x4 0
432.	xy	x 1	x2dx dy 0
	(xy)2 ( y')2 3		x2 y'' y 1

433. Установите соответствие между ДУ и их общими решениями:

y' 5x4 y 0	ln y x5 c
y' 9x8 y 0	ln y	9	x2 c
		2
y' 9xy	ln y x9 c

Найдите в общем решении произвольную постоянную с, соответствующую данному начальному условию для ДУ:

434.y c(x 1)e x ,

нач. условие y(0) 4 для xydx (x 1)dy 0

435.

, нач. условие y( 1) 1

для

cx2

436.

y3 x ce x , нач. условие

y(1) 1 для 3y2 y' y3 x 1

437.

2 y c sin2

x 1, нач. усл.

)

для

y ' (2 y 1)ctgx

Решить задачу Коши: найти общее решение ДУ, а затем, используя начальные данные, выбрать из общего решения частное решение.

Выполнить (где это возможно) проверку определения 12:

438.	xyy'	y2 1 0,	y(e2 ) 0
439.	2x 1	y2 dx ydy 0,		y(1) 0
440.	xy' y 0, y( 2)		4	441. yy' x 0,	y(0) 3

442.ydy xdx 0, y(0) 3

443.xy' y 0, y( 2) 4

444.	(x2 1) y' 2xy2 0,	y(6) 1
445.	x2 y' y 8, y(4) 8	446. 2 y' x y,	y(4) 1

447.x xy y'( y xy) 0, y(0) 0

448.( y2 xy2 )dx (x2 yx2 )dy 0, y(e) e

449.	y ' (2 y 1)ctgx,
449.	y ' (2 y 1)ctgx,	y	0.5
			4
450.	x2 dy y2 dx 0,	y( 1) 1
451.	(1 x2 ) y' y2 1 0,		y( 1) 1.
452.	dy y tgx dx 0,	y( ) 2 .

4.2. Линейные дифференциальные уравнения первого порядка

Опр. 15. Линейным ДУ первого порядка называется ДУ вида:

		y' a(x) y b(x) .			(3)
Решить ДУ:
453.	xy' xy ex , y(1)	e .	454.	xy' 3y x2 ,	y(1) 0 .
455.	( y x2 )dx xdy, y(1) 5 .		456.	y'cos x y sin x sin 2x .
457.	(2x 1) y' y x,	y(0) 5 .

458.y'cos x y sin x 1

459.y' y 2e x , y( 1) 5e .

460.(1 x2 ) y' xy 1, y(0) 5 .

461.xy' y ex , y(a) b .

462.y' 2 y e x , y(0) 5

4.3. Однородные дифференциальныеуравнения первого порядка

Опр.16. Дифференциальное уравнение первого порядка называются од-

		y
нородным, если оно имеет вид y'	f		.

	x

Решить дифференциальное уравнение:

463.

xy' y

xy, y(1) 0 .

464.

, y(1) 1.

465.

xy'cos

y cos

x .

466.

x2 y' y2 xy, y(1) 0.1.

467.

xy' y xtg

468.

xy' 0, y(1) 0 .

469.

xy y2

(2x2 xy) y' .

470.

xy' 2

xy y .

471.

y' x3 y3 .

473.

(x y) y' x y .

472.

y' x2

x .

4.4. Дифференциальные уравнения высших порядков, допускающие понижение порядка

474.y x63 , y(1) 2 , y (1) 1, y (1) 1 .

475.y 4 cos 2x , y(0) 0 , y (0) 0 .

	y					2				1		, y(1) 1,						1			1
					3x4			x3													2 .
476.					3x4			x3								y (1) 3			,	y (1)	2 .
477.	x	4	y			24x			5		6 ,		y( 1) 0 ,							10
477.	x		y			24x					6 ,		y( 1) 0 ,				y ( 1)			10	, y ( 1) 10 .
	y					1
478.			1 x2 .												ln 2
478.			1 x2 .
479.	y					1			,		y					, y			1 .

				cos2				x							2
				cos2				x				4			2			4
	y					1												y'' x sin x
480.			sin2 x .													481.
480.			sin2 x .													481.
482.	y		e			3x	,	y(0) 0					,
482.	y		e				,	y(0) 0					,	y (0) 0 ,			y (0) 0 .
483.	x3 y x2 y 1.															484.		xy y ex x2 .

485. 2x y		y			2	1.	486. x y		y		x 0 .
485. 2x y		y		( y )		1.

487. x	2	y		2	.	488. y y tg x sin 2x .
487. x		y		( y )	.

4.5. Комплексные числа

Изобразить на комплексной плоскости число z и сопряженное ему z :

489.	z 3 4i .	490.	z 3 4i .
491.	z 5 3i .	492.	z 5 3i .
493.	z 2 i .	494.	z 2 i .

Изобразить на комплексной плоскости множество чисел, удовлетворяющих условию:

495. 1 Re z 5 .

Re z 0

497. Im z 0 .

Вычислить число: 499. z i3 .

501. z i6 .

503. z i20 .

496. Im z 0 .

Re z 0

498. Im z 2 .

500. z i5 .

502. z i8 .

504. z i18 .

Вычислить значение функции в точке z0:

505.	f (z) (2 z)2	1,		z0	3 i .
506.	f (z) (2z 1)2 i,			z0	1 i .
507.	f (z) z2 i4 ,	z0	1 i .
508.	f (z) (z 2)2	i6	,	z0 2i 3.

Расположить комплексные числа в порядке возрастания их модулей:


509.	z1	5 2i, z2			5 4i,		z3 i,	z4	1 2i .
510.	z1	6 4i,	z2		3i 4,	z3	i 8,	z4 2i 5 .
511.	z1	i 6,	z2	3i 1, z3		i 2, z4			i .
512.	z1	5i 1,	z2	4i 2, z3			3i 4,		z4 6i .

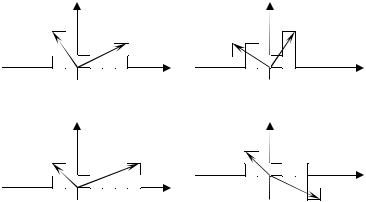
Найти разность комплексных чисел z2 – z1 , изображенных на комплексной плоскости:

513.

514.

z1	z2

z1	z2

515.

516.

z1	z1
z1	z2
	z2

Найти сумму комплексных чисел:
517.	z1	2.5 0.5i , z2 i 1 .	518.	z1 1.5 0.2i , z2 i 2 .
519.	z1	1.5 i , z2 i 3 .	520.	z1 2i 3, z2 0.5i 1 .

4.6. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Написать общее решение ДУ по известным корням характеристического уравнения:

521.	1 2, 2 3.			522.	1	1, 2 4.
523.	1	5, 2	1.	524.	1 2, 2 3.
525.	1 4, 2 4.			526.	1	3, 2 3.
527.	1 2, 2		2.	528.	1 1, 2 1.
529.	1	2i , 2	2i.	530.	1	i , 2 i.
531.	1	i 3, 2 3 i.		532.	1	1 i , 2 1 i.
533.	1	2 4i , 2 2 4i.		534.	1	3 2i , 2 3 2i.

Решить дифференциальные уравнения, сделать проверку:

535. y 4 y 3y 0 .

536. y y 2 y 0 .

537.y 2 y 3y 0, y(0) 1, y'(0) 2 .

538.y y 6 y 0, y(0) 3, y'(0) 4 .

539.y 9 y 0, y(0) 4, y'(0) 9 .

540.y 5y 0, y(0) 1, y'(0) 5 .

541.	y 3y 0 .	542.	y 6 y 0 .
543.	4 y 4 y y 0 .	544.	9 y 6 y y 0 .

545.y 2 y y 0 , y(0) 3, y'(0) 5

546.y 10 y 25y 0, y(0) 3, y'(0) 6

547.	25y 10 y 2 y 0 .	548.	y 2 y 2 y 0 .
549.	9 y 6 y 2 y 0 .	550.	y 14 y 50 y 0 .
551.	y 13y 0	552.	y 49 y 0
553.	y 4 y 13`y 0 .	554.	y 4 y 0 .
555.	y 2 y 5y 0 .	556.	y 4 y 13y 0 .

557.y 9 y 0 , y(0) 1 , y (0) 1.

558.y 4 y 29 y 0 , y(0) 0 , y (0) 15 .

559.9 y y 0 , y( ) 32 , y ( ) 16 .

560.29 y 4 y y 0 , y(0) 0 , y (0) 1029 .

561.y 6 y 13y 0 , y(0) 0 , y (0) 4 .

562.13y 6 y y 0 , y(0) 0 , y (0) 2 .

563.4 y 8y 5y 0 , y(0) 4 , y (0) 0 .

564.5y 8y 4 y 0 , y(0) 5 , y (0) 0 .

Решить линейные неоднородные дифференциальные уравнения:

565.	y y 2 y 9ex .	566. 2 y y y 2e x .
567.	y 2 y 3y e3x y(0) 1,	y'(0) 2
568.	y 3y 2 y 3e2 x y(0) 3, y'(0) 0

y 5 ,4

569.

2 y 3y 5y 7e

571.

y 3y 2 y 4e 2 x .

573.

4 y

e2x

x a2 x2

574.

y 2 y y ex x 2 .

575.

4 y sin 2x ,

576.

y cos3 x .

e2x

577.

4 y

5y cos x .

579.

1 ex .

581.

2 y

y x .

570. y 4 y 5y 6e3x . 572. y 5y 6 y e 2x .


					.
y		4		4	.
		4		4
						1
578.	y		y cos x .
578.	y		y cos x .

580.y 3y 2 y ex1 1 .

582.y y tg x

583.y 4 y 8x3 , y(0) 1 , y (0) 3 .

584.y y x 2ex , y(0) 2 , y (0) 5 .

585.y 3y 9x , y(0) 6 , y (0) 5 .

586.y y 2 y 6x2 , y(0) 1,25 , y (0) 0 .

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20193.73 Mб5РЮМКИН_МАТРИЦЫ_И_ВЕКТОРЫ.doc
#
23.11.201986.53 Кб3с 9 по 13 вопросы.doc
#
30.05.201540.8 Mб47С.Реминный - Тайны кофе разных стран.pdf
#
30.05.201514.87 Mб38Самарский Численные методы.pdf
#
08.05.2019109.57 Кб27Сафронов_пс айкидо.doc
#
30.05.2015457.05 Кб45Сборник задач по высшей математике.pdf
#
23.11.2019337.92 Кб35сборник задач по ПОПД перед2.doc
#
30.05.20151.99 Mб39Сборник статей. Тараканова.pdf
#
30.05.2015701.41 Кб6Сборник-23-х-чтений.docx
#
26.03.20165.6 Mб204СБУ т-3 ред.doc
#
29.04.2019108.54 Кб7Сваровская А. С..doc