
- •Министерство образования и науки рф
- •Национальный исследовательский
- •Томский государственный университет
- •В.И. Рюмкин
- •Матрицы и векторы в экономике
- •1. Матрицы
- •1.1. Определения
- •1.2. Операции над матрицами
- •1.3. Квадратичная форма матрицы. Определенность матрицы
- •1.4. Числовые функции от матриц
- •1.5. Задачи
- •2. Определители
- •2.1. Понятие определителя и его свойства
- •2.2. Алгебраическое дополнение и минор элемента матрицы. Разложение определителей по строке и столбцу
- •2.3. Задачи
- •3. Ранг матрицы
- •3.1. Основные понятия и примеры
- •3.2. Понятия линейной независимости строк и столбцов матрицы. Базис в системе строк (столбцов) матрицы
- •3.3. Методы поиска ранга матрицы
- •3.3.1. Метод окаймляющих миноров
- •3.3.2. Метод элементарных преобразований
- •3.4. Задачи
- •4. Обратная матрица
- •4.1. Основные сведения
- •4.2. Методы поиска обратной матрицы
- •4.2.1. Метод союзной матрицы
- •4.2.2. Метод элементарных преобразований
- •4.3. Задачи
- •5. Векторы
- •5.1. Операции над векторами
- •5.1.1. Алгебраические операции над векторами
- •5.2. Линейная независимость и базис векторов
- •5.3. Геометрическая интерпретация векторов
- •5.3.1. Одномерные, двумерные и трехмерные пространства
- •5.3.2. Многомерные пространства
- •5.4. Задачи
- •6. Линейные преобразования
- •6.1. Основные сведения
- •6.2. Преобразование базиса
- •6.3. Характеристические числа и векторы
- •6.4. Задачи
- •7. Применение векторов и матриц в экономике
- •7.1. Балансовая модель Леонтьева
- •7.2. Модель равновесных цен
- •7.3. Модель международной торговли (модель обмена)
- •7.4. Задачи
- •Литература
- •Оглавление
1.2. Операции над матрицами
Операции
сравнения: матрицы А и В
называются равными (пишут
![]() ),
если они имеют одинаковый порядок и все
их элементы с одинаковыми индексами
равны:
),
если они имеют одинаковый порядок и все
их элементы с одинаковыми индексами
равны:
![]() .
.
Говорят,
что матрица A больше
матрицы B (пишут
![]() ),
если они имеют одинаковый порядок,
причем
),
если они имеют одинаковый порядок,
причем
![]() .
.
Операция
сложения: суммой
![]() двух матриц A и B
одного и того же порядка
называется матрица C
того же порядка, элементы которой
определяются формулами
двух матриц A и B
одного и того же порядка
называется матрица C
того же порядка, элементы которой
определяются формулами
![]() .
.
Пример
1.2. Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
Операция
умножения матрицы на число: любую
матрицу A можно умножить
на произвольное число k
как слева, получив матрицу
![]() ,
так и справа, получив матрицу
,
так и справа, получив матрицу
![]() .
При этом матрицы B и
C равны между собой,
имеют тот же порядок, что и матрица A.
Элементы матриц
и
определяются формулами
.
При этом матрицы B и
C равны между собой,
имеют тот же порядок, что и матрица A.
Элементы матриц
и
определяются формулами
![]() .
.
Пример
1.3. Пусть
,
![]() .
Тогда
.
Тогда
![]() .
.
Свойства операций сложения и умножения матриц на число
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]() ,
,
5.
![]() ,
,
6.
![]() .
.
Операция
вычитания матрицы B
из матрицы A определяется
следующим образом:
![]() .
Матрица
.
Матрица
![]() называется матрицей, противоположной
матрице A.
называется матрицей, противоположной
матрице A.
Операция
умножения матрицы на матрицу:
произведением
![]() матрицы A на матрицу
B называется матрица
C, элементы которой
определяются формулами
матрицы A на матрицу
B называется матрица
C, элементы которой
определяются формулами
![]() ,
,
где
![]() число
элементов в строках матрицы A
и в столбцах матрицы B.
Произведение
имеет столько же строк, сколько левый
сомножитель A и столько
же столбцов, сколько правый сомножитель
B.
число
элементов в строках матрицы A
и в столбцах матрицы B.
Произведение
имеет столько же строк, сколько левый
сомножитель A и столько
же столбцов, сколько правый сомножитель
B.
Пример
1.4. 1) Пусть
,
.
Тогда
![]()
![]() .
.
2)
Пусть
![]() ,
,
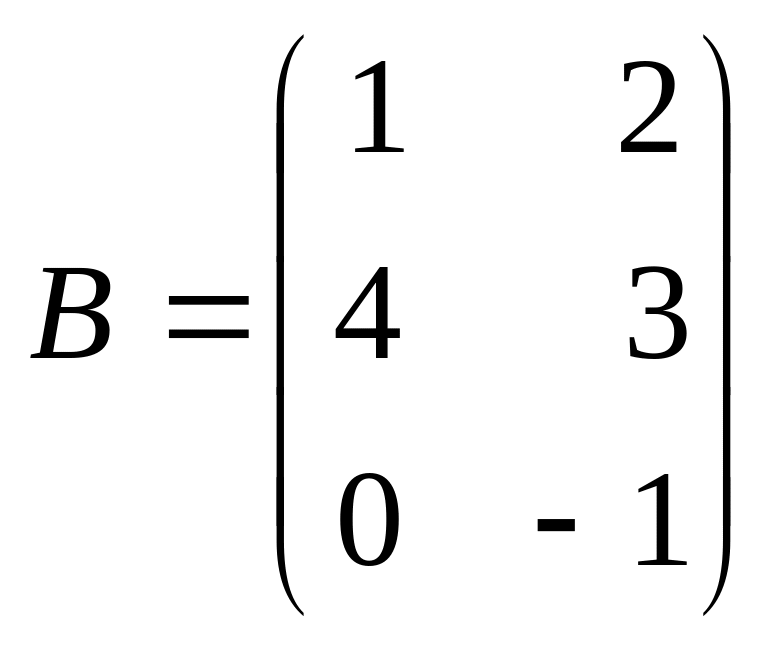 .
Тогда
.
Тогда
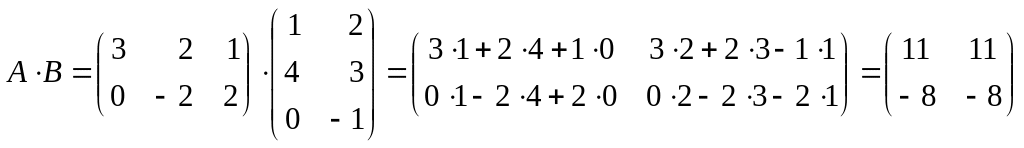 ;
;
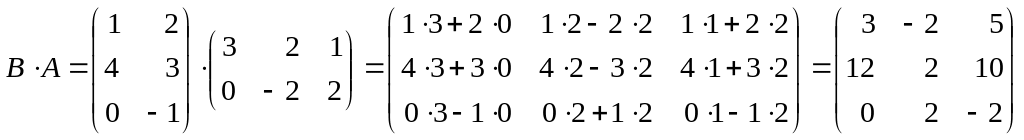 .
.
В
общем случае
![]() .
Матрицы A и B,
для которых
.
Матрицы A и B,
для которых
![]() ,
называются коммутативными
(перестановочными). Единичная и нулевая
матрицы коммутативны с любой матрицей,
на которую их можно умножить.
,
называются коммутативными
(перестановочными). Единичная и нулевая
матрицы коммутативны с любой матрицей,
на которую их можно умножить.
Свойства операции умножения матрицы на матрицу
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]() ,
,
5.
![]() ,
,
6.
![]() .
.
Операция
возведения матрицы в степень. Пусть
k есть целое
неотрицательное число. Тогда k-й
степенью
![]() матрицы A называется
результат умножения матрицы A
самой на себя k раз.
По определению полагаем:
матрицы A называется
результат умножения матрицы A
самой на себя k раз.
По определению полагаем:
![]()
Число k при этом называется показателем степени.
Свойства операции возведения матрицы в степень
1.
![]() ,
,
2.
![]() .
.
Пример
1.5. Пусть
![]() .
Тогда
.
Тогда
![]() ;
;
![]() ;
;
![]() .
.
Операция
транспонирования матрицы. Пусть
![]() произвольная матрица порядка
.
Матрица
произвольная матрица порядка
.
Матрица
![]() ,
состоящая из элементов, удовлетворяющих
условию
,
состоящая из элементов, удовлетворяющих
условию
![]() ,
называется транспонированной матрицей
A и обозначается
,
называется транспонированной матрицей
A и обозначается
![]() .
Строки матрицы
состоят из элементов столбцов матрицы
A, а столбцы – из
элементов строк матрицы A:
.
Строки матрицы
состоят из элементов столбцов матрицы
A, а столбцы – из
элементов строк матрицы A:
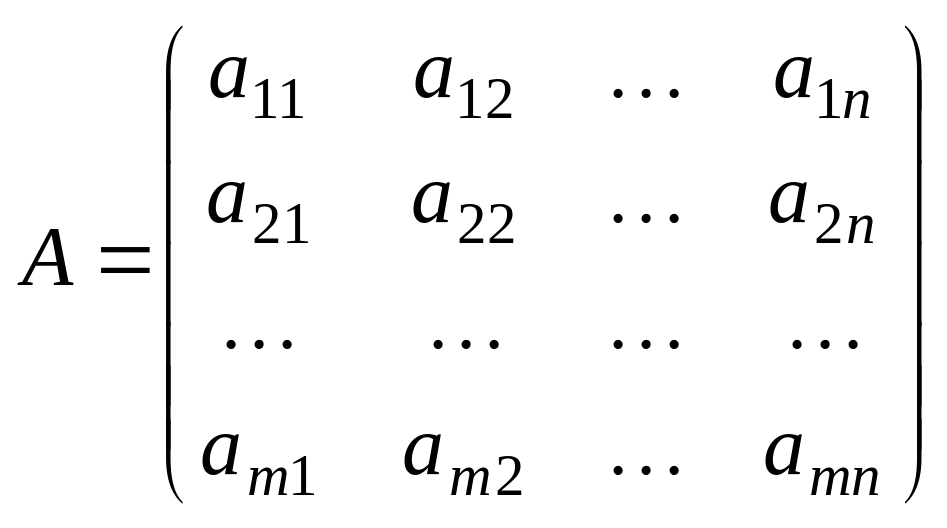
![]()
 .
.
Свойства операции транспонирования матрицы
1.
![]() ,
,
2.
![]() .
.
Пример
1.6. Пусть
![]() .
Тогда
.
Тогда
 .
.
Операции элементарных преобразований над матрицами. Специальный класс операций над матрицами представляют операции, называемыми элементарными преобразованиями. К элементарным преобразованиям относятся следующие операции над матрицами:
1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля. Все другие элементы матрицы при этом остаются неизменными.
2) прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой ее строки (столбца), умноженных на одно и то же произвольное число. Все другие элементы матрицы при этом остаются неизменными.
3) перестановка двух каких-либо строк (столбцов) матрицы местами.
Теорема о представлении элементарных преобразований матриц операциями умножения. Справедливы следующие утверждения.
1.
Умножение i-й
строки матрицы
![]() на число
на число
![]() эквивалентно операции умножения
эквивалентно операции умножения
![]() на эту матрицу слева квадратной матрицы
на эту матрицу слева квадратной матрицы
![]() вида
вида
 (1.1)
(1.1)
(число находится в i-й строке и i-м столбце; все остальные элементы – как в единичной матрице).
2.
Прибавление к i-й
строке матрицы
ее j-й строки,
умноженной на число
![]() ,
эквивалентно операции умножения
на эту матрицу слева квадратной матрицы
L вида
,
эквивалентно операции умножения
на эту матрицу слева квадратной матрицы
L вида
 (1.2)
(1.2)
(число
![]() находится в i-й
строке и j-м столбце;
все остальные элементы – как в единичной
матрице).
находится в i-й
строке и j-м столбце;
все остальные элементы – как в единичной
матрице).
3. Перестановка строк матрицы местами может быть осуществлена конечной последовательностью умножений на эту матрицу слева специальных матриц вида (1.1) и (1.2).
Пример
1.7. Пусть
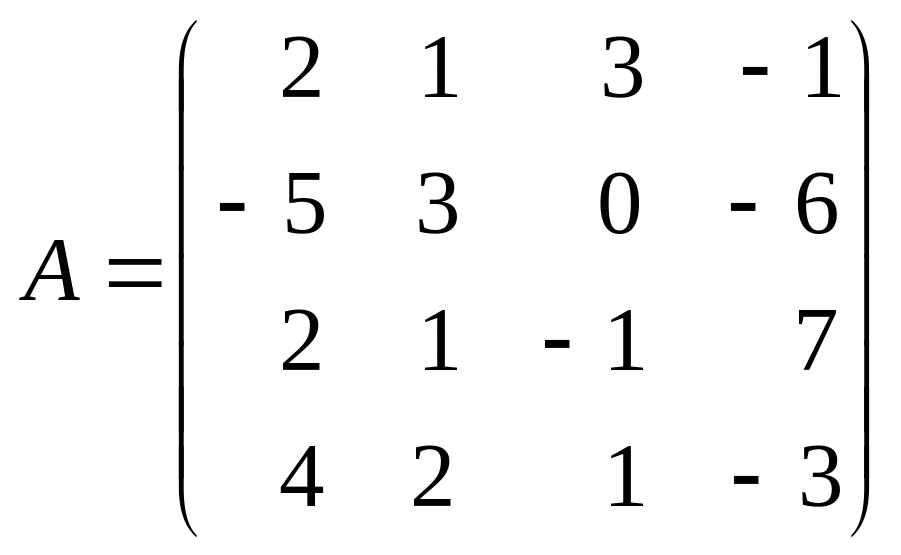 .
Тогда справедливы следующие представления:
.
Тогда справедливы следующие представления:
а) умножение третьей строки матрицы A на 4:
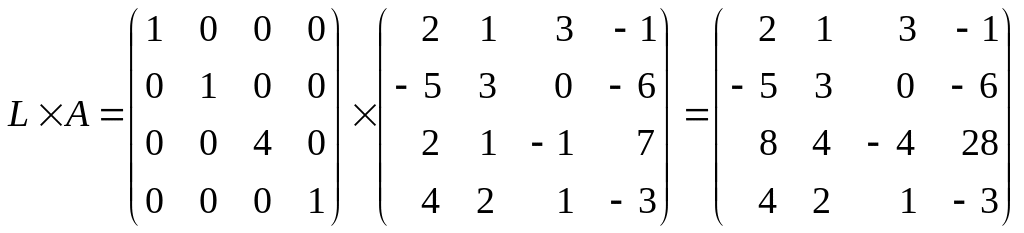 .
.
б) прибавление ко второй строке матрицы А ее четвертой строки, умноженной на 3:
 .
.
в) смена местами первой и третьей строк матрицы А:
1)
прибавление к третьей строке матрицы
А ее первой строки, умноженной на
–1, то есть
![]() :
:
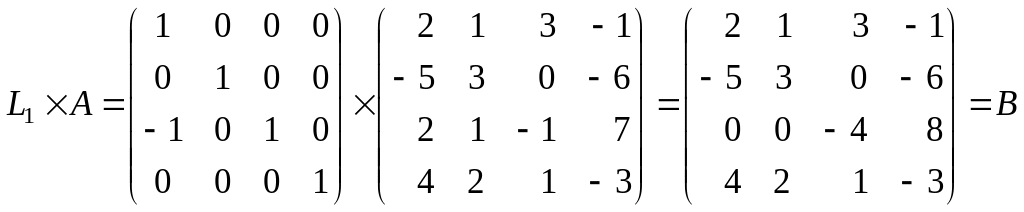 ;
;
2)
прибавление к первой строке полученной
матрицы В ее третьей строки, умноженной
на 1:
![]() :
:
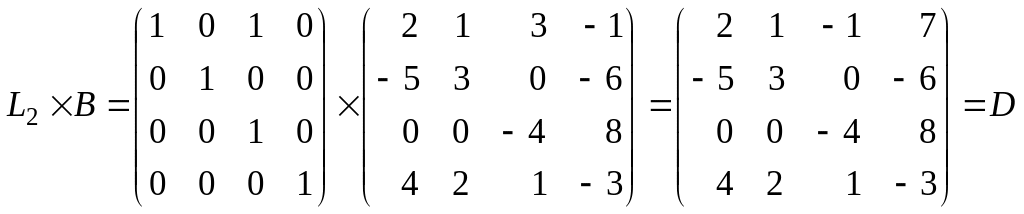 ;
;
3)
прибавление к третьей строке полученной
матрицы D ее первой
строки, умноженной на –1, то есть
![]() :
:
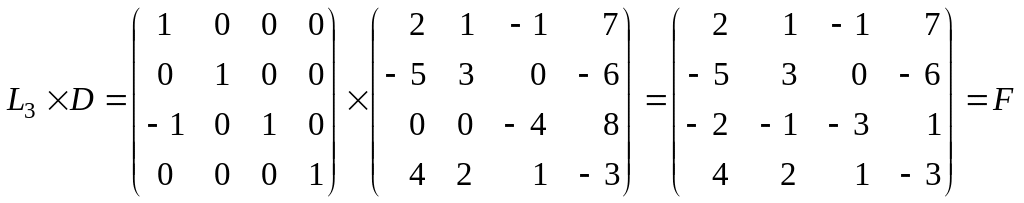 ;
;
4)
умножение третьей строки полученной
матрицы F на –1, то есть
![]() :
:
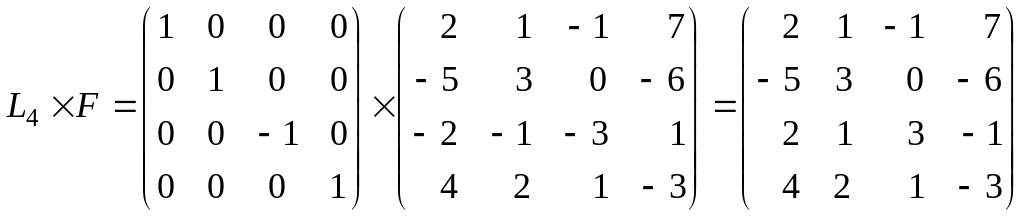 .
.
Таким
образом, к смене мест первой и четвертой
строк матрицы А ведет следующее
преобразование:![]() ,
,
где
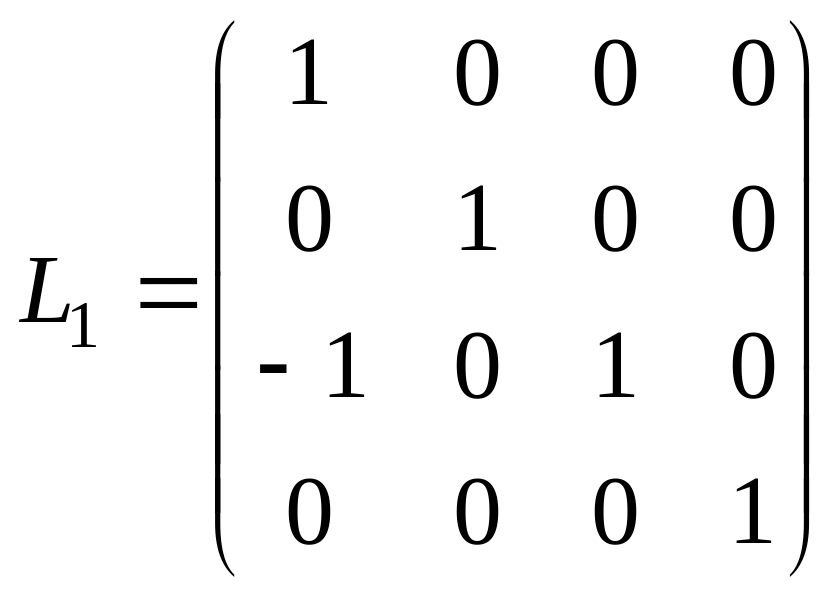 ;
;
 ;
;
 ;
;
 .
.
