
- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •[§3.] Принцип неопределенности
- •[§4.] Полный набор динамических переменных
- •[§5.] Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •[§7.] Волновая функция и ее свойства
- •[§8.] Принцип суперпозиции состояний
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •[§15.] Операторы координаты , импульса , момента импульса , энергии .
- •[§ 19.] Волновое уравнение
- •[§ 24.] Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •[§ 28.] Собственный механический момент (спин)
- •§1. Статистическое описание систем с большим числом степеней свободы
- •§3. Микро- и макро- параметры системы.
- •§4. Свойство эргодичности системы.
- •§5. Два способа усреднения в статистической физике
- •§6. Понятие ансамбля систем
- •§7. Эргодическая гипотеза
- •§8. Равновесное состояние системы
- •§10. Квазизамкнутость и статистическая независимость подсистем
- •§15. Микроканоническое распределение Гиббса
- •§16. Каноническое распределение Гиббса
- •§21*. Распределение Максвелла как следствие канонического распределения Гиббса
- •§23. Большое каноническое распределение
- •§25. Распределение Ферми-Дирака
- •§26. Распределение Бозе-Эйнштейна
§ 25. Стационарное состояние различных систем
Задача на собственные функции и собственные значения для оператора :
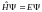 (25.1)
(25.1)
Волновое уравнение:
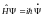 (25.2)
(25.2)
Как только поставили в соответствие системе оператор , то можем решать волновое уравнение, находим , которая определяет состояние системы.
Собственные функции задачи (25.1) и функции, являющиеся решением волнового уравнения совпадают при условии выполнения:
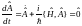
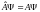
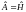 ,
тогда
,
тогда
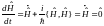 . Это условие совместности решений
(25.1) и (25.2).
. Это условие совместности решений
(25.1) и (25.2).
Так
как
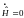 ,
то гамильтониан системы явно от времени
не зависит, т. е. поле стационарно (задача
стационарна) – это говорит о совместности
решений (25.1) и (25.2).
,
то гамильтониан системы явно от времени
не зависит, т. е. поле стационарно (задача
стационарна) – это говорит о совместности
решений (25.1) и (25.2).
Рассмотрим стационарную задачу , тогда не зависит от времени. Это либо:
Замкнутая система.
Система в стационарном внешнем поле.
Используя (25.1) и (25.2), получим
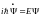
Это дифференциальное уравнение имеет решение

Подставим эту функцию в (25.1), тогда
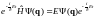 .
.
Тогда получим
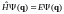
Получили стационарное уравнение Шредингера.
[§ 28.] Собственный механический момент (спин)
Рассмотрим Na. У него есть желтая линия . Возникает при переходе с уровня 3p на 3s.
Первоначально
ее длина была 5892
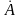
Было обнаружено, что эта линия расщепляется на две: дублет.
Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.
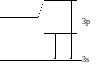
Их длины: 5896 и 5890 .
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.
У
электрона спиновое число s=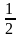 .
.
Впоследствии Паули ввел спин в теорию.
Если
имеем одну частицу, то она характеризуется
орбитальным квантовым числом
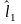 .
.
Составная частица (атом) состоит из
многих микрочастиц. Можно рассматривать
эту составную частицу вцелом и приписать
ей момент
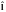 ,
который описывает орбитальное движение
частицы как целого.
,
который описывает орбитальное движение
частицы как целого.
Энергетический уровень этой составной
частицы в некоторых полях будет зависеть
от орбитальных моментов микрочастиц
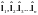 .
.
Эти моменты являются внутренним свойством этой составной частицы.
Можно рассматривать 2 момента:
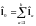 .
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)
.
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)Частица сама движется по некоторой траектории.
У частицы есть еще квантовое число
 ,
характеризующее собственный механический
момент.
,
характеризующее собственный механический
момент.
Вводят оператор собственного механического момента:
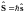
По аналогии
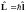
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.
§1. Статистическое описание систем с большим числом степеней свободы
Статистическая
физика изучает системы с большим числом
степеней свободы. Наличие большого
число степеней свободы вносит некоторые
особенности в описание таких систем.
Например, в
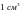 воздуха
содержится ~
2.7,·1019
частиц (число Лошмидта), но
у каждой материальной точки (частицы)
имеется 3 степени свободы, поэтому у
этой системы огромное число степеней
свободы.
воздуха
содержится ~
2.7,·1019
частиц (число Лошмидта), но
у каждой материальной точки (частицы)
имеется 3 степени свободы, поэтому у
этой системы огромное число степеней
свободы.
В классической механике возможно
описывать такие системы (через формализм
Гамильтона) -
динамических переменных
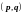 ,
где
,
где
 - число степеней свободы. Описание
системы сводится к решению уравнений:
- число степеней свободы. Описание
системы сводится к решению уравнений:
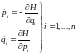
Чтобы решить данную систему, необходимо задать начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности(долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, т.е. детерминированный подход здесь не используют.
Статистическая физика рассматривает
переход от малого числа степеней свободы
к большому.
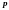 и
и
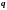 - это динамические переменные. Фазовое
пространство – это
мерное пространство, декартовыми осями
которого являются переменные
- это динамические переменные. Фазовое
пространство – это
мерное пространство, декартовыми осями
которого являются переменные
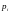 и
и
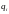 .
Тогда состояние системы (которое задаётся
динамическими переменными) в фазовом
пространстве задаётся фазовой точкой.
Движение системы в реальном пространстве
задаётся движением фазовой точки в
фазовом пространстве, т.е. устанавливается
соответствие между фазовым и реальным
пространствами.
.
Тогда состояние системы (которое задаётся
динамическими переменными) в фазовом
пространстве задаётся фазовой точкой.
Движение системы в реальном пространстве
задаётся движением фазовой точки в
фазовом пространстве, т.е. устанавливается
соответствие между фазовым и реальным
пространствами.
