- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •[§3.] Принцип неопределенности
- •[§4.] Полный набор динамических переменных
- •[§5.] Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •[§7.] Волновая функция и ее свойства
- •[§8.] Принцип суперпозиции состояний
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •[§15.] Операторы координаты , импульса , момента импульса , энергии .
- •[§ 19.] Волновое уравнение
- •[§ 24.] Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •[§ 28.] Собственный механический момент (спин)
- •§1. Статистическое описание систем с большим числом степеней свободы
- •§3. Микро- и макро- параметры системы.
- •§4. Свойство эргодичности системы.
- •§5. Два способа усреднения в статистической физике
- •§6. Понятие ансамбля систем
- •§7. Эргодическая гипотеза
- •§8. Равновесное состояние системы
- •§10. Квазизамкнутость и статистическая независимость подсистем
- •§15. Микроканоническое распределение Гиббса
- •§16. Каноническое распределение Гиббса
- •§21*. Распределение Максвелла как следствие канонического распределения Гиббса
- •§23. Большое каноническое распределение
- •§25. Распределение Ферми-Дирака
- •§26. Распределение Бозе-Эйнштейна
§21*. Распределение Максвелла как следствие канонического распределения Гиббса
Далее
будем излагать без константы
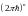 ,
т.к. она нам в ближайших расчётах не
понадобится.
,
т.к. она нам в ближайших расчётах не
понадобится.
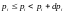
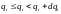
здесь
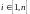 ,
а
- число степеней свободы.
,
а
- число степеней свободы.
В квазиклассике:
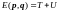
Рассмотрим
систему из
материальных точек и в качестве
степеней свободы выберем
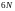 переменных:
переменных:
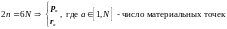
т.е. это обычное трехмерное пространство.
Тогда можем в явном виде записать кинетическую энергию и аргументы потенциальной энергии:
 и
и
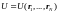
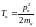
здесь время отсутствует, потому что решается стационарная задача.
И функция плотности вероятности и вероятность зависят от всех выше указанных переменных:
 (15)
(15)
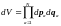
Каждый
вектор
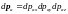 - т.е. это элементарный объём соответствующего
трёхмерного пространства.
- т.е. это элементарный объём соответствующего
трёхмерного пространства.
Вероятность
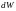 говорит
о событии:
говорит
о событии:
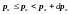
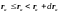
где
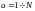 .
.
Если имеем вероятность некоторого совместного события:
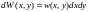
то вероятность одного из них:
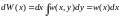
тогда:
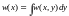 (16)
(16)
Используем соотношение (16), чтобы, зная вероятность (15), найти плотность распределения импульсов (в данном случае импульса первой точки):
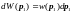
Аналогично (16) получаем:
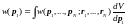 здесь
здесь
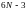 интегралов
интегралов
Для
функции
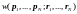 имеем:
имеем:
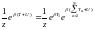
При
интегрировании функция
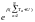 даст константу, а
даст константу, а
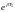 выносится за интеграл тогда:
выносится за интеграл тогда:
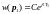
Из условия нормировки найдём константу :
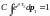
Далее индекс «1» ставить не будем, т.к. если все точки одинаковы, то нет смысла выделять точку (для всех точек распределение будет одинаковое).
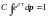 и
и
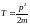
(Далее Т – температура)
Тогда:
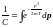
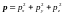 ,
а
,
а
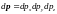
все
переменные меняются в пределах от
 до
до
 ,
тогда получаем:
,
тогда получаем:
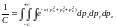
где
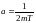
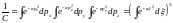
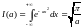
Тогда получаем:
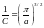
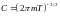
Само распределение имеет вид:
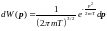
Мы получили распределение вероятностей импульсов или распределение Максвелла. Хотя его ещё называют распределением Больцмана.
Эта вероятность говорит о событии:
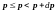
здесь три неравенства, т.к. имеется три проекции импульса.
§23. Большое каноническое распределение
Запишем первое начало термодинамики, при учёте, что происходит обмен частицами:
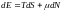
где
-
число частиц, а
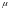 - химический потенциал.
- химический потенциал.
П усть
между системами 1 и 2 идёт обмен частицами
(материальный контакт) и энергетический
контакт (теплой обмен).
усть
между системами 1 и 2 идёт обмен частицами
(материальный контакт) и энергетический
контакт (теплой обмен).
Для энтропии можем записать:
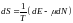
Ранее мы писали соотношение:
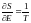
Теперь добавим туда и перепишем его:
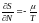
Поступая аналогично случаю теплового контакта, мы получаем, что равновесие при тепловом и материальном контакте наступает при
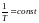 и
и
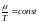 ,
т.е.
,
т.е.
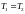 и
и
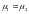
Аналогично получают большое каноническое распределение:
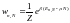
система находится в квантовом состоянии и имеет частиц.
В данном случае система находится в тепловом и материальном контакте.
Еще большое каноническое распределение называют распределением Гиббса с переменным числом частиц.
Здесь
статистическая сумма
 и
и
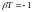 .
.
- набор квантовых чисел, характеризующих состояние системы.
§25. Распределение Ферми-Дирака
Чтобы
получить распределение Ферми-Дирака
надо посчитать термодинамический
потенциал
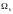 :
:
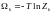
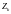 - одночастичная большая статистическая
сумма.
- одночастичная большая статистическая
сумма.
И с помощью посчитаем число состояний с учетом свойств Ферми-частиц.
Напомним, что:
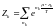
здесь отсутствует взаимодействие между частицами, но имеет место обменное взаимодействие, т.е. за счёт спина (влияние сорта частиц на результат)
Для
Ферми-частиц
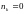 либо 1.
либо 1.
Рассчитаем для Ферми-газа:
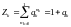
где
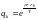 .
.
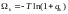
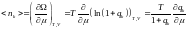
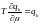
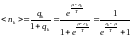
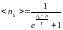
Мы получили распределение Ферми-Дирака. Это среднее число Ферми частиц в -том состоянии.
Придадим
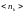 другой смысл. По определению:
другой смысл. По определению:
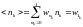
Таким образом, это вероятность обнаружить одну Ферми частицу в -том состоянии: