2. Экстремумы функции нескольких переменных.

Пусть дана дважды непрерывно дифференцируемая функция двух переменных.

Теорема 4. (Необходимое условие локального экстремума дифференцируемой функции )

Если – ( точка экстремума функции f, то

Теорема 3. (Достаточные условия локального экстремума дважды дифференцируемой функции )

Обозначим A= ( ; B= ( ; C= . Тогда, если

D= , D=АС-В²

1. Если D < 0, экстремума функции f в точке ( нет;

2. Если D > 0, то в точке ( - экстремум функции f причем если

а)A > 0, то ( - точка минимума;

б) A < 0, то ( - точка максимума. 

3. Если D = 0, необходимы дополнительные исследования.

Теорема 4. (Необходимый признак экстремума функции многих переменных.) Если точка x⁰=(х₁⁰,…, х_n⁰) является точкой экстремума функции, то частные производные в этой точке равны нулю или не существуют, т. е. если для всех i=1,…,n

или не существует.

Точки, в которых все частные производные равны нулю, называются стационарными точками.

Пусть x - стационарная точка. Достаточный признак локального минимума функции многих переменных заключается в выполнении неравенств

,

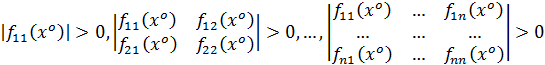а достаточный признак локального максимума функции многих переменных заключается в выполнении неравенств

.

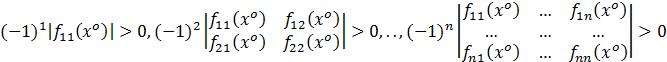Если требуется найти наибольшее (или наименьшее) значение функции f при х=(х₁,…, х_n) (задача с ограничениями), то аналогично тому, как это делалось для функции одной переменной, находятся экстремумы функции внутри области М и экстремумы функции на границе области М и среди них выбирается наибольшее (наименьшее) значение. Кроме того, у ограничений типа равенства можно выразить одни переменные через другие и тем самым уменьшить число переменных, что облегчает решение задачи.

Так же, как и у функции одной переменной: если критическая точка одна, то если это будет точка локального максимума (минимума) – она будут являться точкой наибольшего наименьшего) значения функции.

З

l

адача 3.1.Сечение канала имеет форму равнобочной

т

рапеции данной площади. Какими выбрать его размеры,

ч

Рис. 1

а

тобы омываемая площади канала была наименьшей?

Решение. Очевидно, верхняя часть сечения канала равна a+2l а высота равна l . Поэтому площадь поперечного сечения канала S находим по формуле

S= . (3)

Если р- длина канала, то омываемая площадь канала F=p(a+2l). Так как р- постоянная, то минимум функции F будет совпадать с минимумом функции

f=a+2l (4)

Таким образом, математическая модель задачи: найти а и l, доставляющие наименьшее значение целевой функции (4) при выполнении условия (3). Кроме того, очевидно,

(5)

Из (3) выразим переменную

a= (6)

и, подставляя в(2), получим

f= .

, + l .

Частные производные существуют во всех точках области (5). Найдем стационарные точки, решая систему

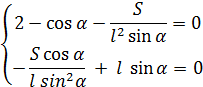
Из второго уравнения

l . (7)

Подставляя это выражение в первое уравнение, получим

Отсюда,

Из (7) найдем или

l= . (9)

Из (6) найдем а

а= ,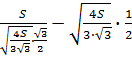

откуда находим

а= . (10)

Из (9) и (10) следует а= l.

Таким образом, мы получили единственную стационарную точку функции f : ( ).

Определим характер этой точки, используя достаточные условия экстремума.

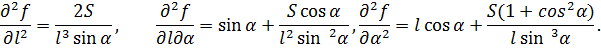
, С=

Так как А , то рассматриваемая точка локального минимума функции f . Поскольку стационарная точка единственная, то она будет являться точкой наименьшего значения функции f.

Таким образом, оптимальная конфигурация канала: а=l и