2.4. Необходимые сведения из матричной алгебры

Методы матричной алгебры широко используются в экономике. Матричное исчисление применяется при анализе межотраслевого баланса, при анализе регрессионных уравнений, в факторном и дисперсионном анализах и т.д..С помощью матричной алгебры громоздкие системы уравнений могут быть записаны в виде простых и компактных формул.. Универсальный характер матричных выражений позволяет приложить одни и те же методы анализа и к малому, и к большому массивам исходных данных .

Матрицей называется прямоугольная таблица, составленная из чисел. Размером матрицы называется пара чисел m×n, где m – число строк, а n – число столбцов таблицы. Числа, составляющие матрицу, называются ее элемента ми .

Матрица размером n×n называется квадратной.

Над матрицами можно производить ряд операций.

Матрицу можно умножить на число.

A = C, где A = {a_ij}, С = { a_ij}

Матрицы одинакового размера можно складывать и вычитать.

A + B = C, где A = {a_ij}, B = {b _ij}, C = {c_ij = a_ij + b _ij}

A - B = C, где A = {a_ij}, B = {b _ij}, C = {c_ij = a_ij - b _ij}

Матрицу A размером m×n и матрицу B размером n×k можно перемножать, в результате получается матрица C размером m×k

A B = C, где A = {a _ij}, B = {b _ij}, C = { = c _ij}.

Произведение матрицы A на вектор x является вектором y, т.е. y = Ax.

Транспонированная матрица есть матрица А^Т , столбцы которой являются строками исходной матрицы при сохранении их порядка. Транспонирование вектор-столбца дает вектор-строку и наоборот. Матрица называется симметрической, если транспонированная матрица равна самой матрице.

Диагональная и единичная матрицы.

Матрица, результат умножения которой на матрицу A равна единичной матрице, называется обратной к A и обозначается символом A^–1 .

Для получения обратной матрицы необходимо:

1) найти определитель исходной матрицы det A;

2) найти матрицу М из алгебраических дополнений к каждому элементу матрицы А^Т ;

3) найти А^–1 = М / det A.

2.5. Системы линейных алгебраических уравнений

Очень удобно записывать системы линейных алгебраических уравнений с помощью матриц.

Пусть А= , тогда запись

АХ=В (5)

по правилу произведения матриц

,

что эквивалентно системе уравнений

(6)

Из (5) следует формула для решения системы (6)

Х=А^-1В. (7).

Однако эта формула применима только в том случае, когда матрица А квадратная (т.е. число уравнений равно числу неизвестных) и имеет обратную (т.е. detA Этих недостатков лишен метод Гаусса, в котором рассматривается расширенная матрица

.

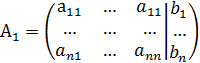Пример 2.1. Решить систему линейных алгебраических уравнений

.

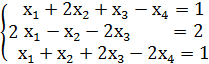Составим из нее расширенную матрицу

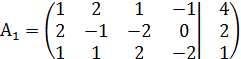
и приведем ее к треугольному виду . Для этого сначала получим нули в первом столбце во второй и третьей строке. Для получения 0 во второй строке умножим элементы первой строки на (- и прибавим к элементам второй строки. Для получения 0 в третьей строке умножим элементы первой строки на (- 1) и сложим с элементами третьей строки. Получим

.

Умножив вторую строку на (- и сложив ее с элементами третьей строки, получим 0 во втором столбце третьей строки

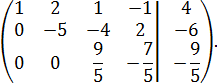
Из третьей строки матрицы получаем уравнение

,

и, выражая , будем иметь

.

Из второй строки матрицы получим уравнение

-5 - 4 +2 =-6,

откуда

Из первой строки матрицы

и, выражая

=1+

Таким образом, мы получили решение системы уравнений

(1+ ; ; ; ), где - любое число.

Итак, наша система линейных алгебраических уравнений имеет бесчисленное множество решений. Переменные , , выражаются через переменную Такие переменные, которые выражаются через другие переменные – называют базисными переменными, а переменные, через которые выражены базисные переменные (у нас , называют свободными переменными.