6.Симплекс-метод решения задачи линейного программирования.

6.1. Выпуклые многогранники.

Пусть мы имеем ограничения, заданные в виде системы линейных алгебраических уравнений

(1)

где n>m. Если ранг данной системы линейных алгебраических уравнений равен m, то система имеет бесчисленное множество решений, причем m переменных (базисные переменные) можно выразить через оставшиеся переменные (свободные переменные) Будем считать переменные базисными, переменные – свободными. В линейной алгебре доказывается, что множество решений системы (1) ( является выпуклым многогранником, а точка ( - угловой точкой. Если в качестве базовых переменных взять другие переменные, а все свободные переменные положить равными нулю, то получим другую угловую точку многогранника. Таким образом, общее число всех угловых точек С_n^m.

Рассматривая решение задач графическим методом, мы видели, что оптимальное решение (если оно существует) определяется некоторой угловой точкой (или двумя угловыми точками – тогда и весь отрезок прямой, соединяющий эти точки, будет состоять из точек, являющихся оптимальным решением). Отметим, что и в общем случае это утверждение справедливо.

Таким образом, мы должны определить значение критерия качества в угловых точках и найти такую, в которой он принимает наибольшее (наименьшее значение). Сделать это можно с помощью симплекс-метода.

6.2.Симплекс-метод. Пример.

Решим теперь задачу, которую мы решали геометрическим методом, другим способом, не использующим геометрическую интерпретацию. Для этого нам будет удобно обозначить х= , у= . Тогда f( = , а ограничения будут иметь вид

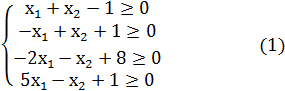
Перейдем от ограничений в виде неравенств к ограничениям в виде равенств

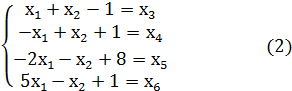
(3)

f( = mах.

Мы уже отмечали, что решение задачи линейного программирования будет находиться в угловой точке области М. По терминологии, принятой в алгебре и которой мы будем пользоваться, переменные называются базисными переменными ( так как они выражаются через ) а переменные называют свободными переменными.

Угловые точки области М – точки пересечения прямых, задаваемых ограничениями (2) и (3). Одной из граничных точек будет точка, в которой Однако в этом случае из (2) мы получим , чего не может быть по условиям (3). Поэтому нам нужно в качестве свободных переменных выбрать другие переменные, так чтобы свободные члены в (2) были неотрицательны.

Возьмем в качестве свободных переменных Для этого в системе (2) выразим через Получим следующую систему

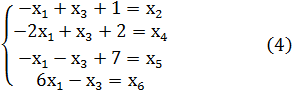
Выразим через новые переменные целевую функцию

f=( = = - . (5)

Из (4) видно, что все переменные неотрицательны при Такую систему ограничений в которой все свободные члены неотрицательны, называют системой ограничений в допустимом виде.

Как видно из (5) при увеличении целевая функция может только лишь уменьшаться, а при увеличении - увеличиваться (так как коэффициент при положителен). Поэтому для увеличения f нам нужно увеличивать При система (4) примет вид

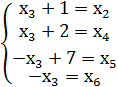
Если , то из первых двух уравнений имеем В тоже время, только при 0 , а

Так как при увеличении нарушаются условия (3), то вместо свободной переменной нужно вводить новую свободную переменную Выразим переменные через новые свободные переменные Получим систему уравнений

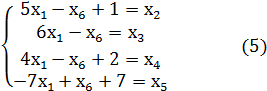
и целевую функцию

f=2+11 . (6)

При увеличении в (6) f может только лишь уменьшаться, а при увеличении - увеличиваться. Положим в (5) и будем увеличивать (5) примут вид

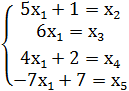
В первых трех уравнениях при Однако только при . Переведем вместо в свободную переменную

Получим систему

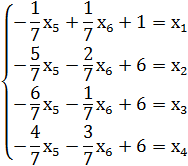
А f=13- .

Очевидно f принимает наибольшее значение при ., f(0,0) = 13.

При этом