4. Симплекс-таблицы. Пример.

Наиболее трудоемкая часть при работе с симплекс методом – выражать одни переменные через другие. Этот процесс можно значительно упростить, применяя метод, аналогичный методу Гаусса при решении систем линейных алгебраических уравнений.

Рассмотрим тот же пример, который мы рассматривали при решении геометрическим методом. (задача (4)-(5) в ) Требуется найти наибольшее значение функции

f( = - . (1)

при ограничениях

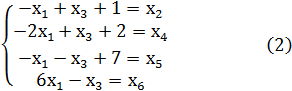
и , j=1,…,6

Напомним, что , , – базисные переменные, а и - свободные.

Запишем (2) в виде

а целевую функцию (1) в виде

f + . (4)

Занесем коэффициенты при в таблицу, которую называют сииплекс- таблицей.

Базисные переменные	Свободные члены
	1	1	1	-1	0	0	0
	2	2	0	-1	1	0	0
	7	1	0	1	0	1	0
	0	-6	0	1	0	0	1
Форма f	2	1	0	-2	0	0	0

Так как базисные переменные входят в каждое из уравнений системы (3) по одному разу, то в каждом столбце базисных переменных стоит одна единица, а остальные – нули. Это характерные признак базисной переменной.

Поскольку в (4) мы перенесли переменные в левую часть, то в строке формы f мы ищем не положительные, а отрицательные коэффициенты при переменных отрицательный знак будет у , поэтому этот столбец отмечаем стрелкой.

В столбце, соответствующем ищем положительные коэффициенты (а не отрицательные, как мы делали в симплекс-методе, так как переменные мы также переносили в другую часть равенства). Таких коэффициентов два (у и ). В таких случаях договоримся, как и в.симплекс-методе (хотя это и не обязательно) брать ту переменную, у которой отношение свободного члена к коэффициенту меньше. У переменной это будет , а у -

Поэтому выбираем переменную и соответствующую строку обозначаем стрелкой. Итак, мы будем переводить в базисную переменную, а в свободные переменные. Чтобы стала базисной переменной нам нужно получить в столбце для все нули и одну единицу, стоящую на месте пересечения помеченных строки и столбца. Это делается также, как и в методе Гаусса, помеченную строку мы можем умножить на любое число(отличное от нуля) и сложить с другой строкой. Полученная при этом система ограничений буде эквивалентна предыдущей.

Поэтому для получения нулей в столбце

1. Прибавляем помеченную строку к первой строке;

2. Прибавляем помеченную строку к второй строке;

3. Прибавляем помеченную строку, предварительно умножив ее на (-1), к третьей строке;

4. Прибавляем помеченную строку, предварительно умножив ее на 2, к пятой строке;

В столбце для базисных переменных вместо пишем , так как она стала теперь базисной переменной.

В результате получаем симплекс-таблицу.

Базисные переменные	Свободные члены
	1	-5	1	0	0	0	1
	2	-4	0	0	1	0	1
	7	7	0	0	0	1	- 1
	0	-6	0	1	0	0	1
Форма f	2	-11	0	0	0	0	2

Отрицательный коэффициент в строке формы f при . Помечаем этот столбец стрелкой.

В столбце, соответствующем ищем положительные коэффициенты. Такой коэффициент будет у Строку, соответствующую переменной , обозначаем стрелкой. Произведем замену базисно переменной на . Однако нам нужно, чтобы на пересечении помеченных столбца и строки стояла 1. Для этого отмеченную строку делим на 7. Далее:

1. Умножаем отмеченную строку на 5 и складываем с первой,

2. Умножаем отмеченную строку на 4 и складываем со второй,

3. Умножаем отмеченную строку на 6 и складываем с четвертой,

4. Умножаем отмеченную строку на 11 и складываем с пятой.

Получим следующую таблицу.

Базисные переменные	Свободные члены
	6	0	1	0	0
	6	0	0	0	1
	1	1	0	0	0
	6	0	0	1	0
Форма f	13	0	0	0	0

Строка, соответствующая форме f, даст

f + + = 13 или f =13- -

Так как , то наибольшее значение форма f получит при , тогда

=1, =6.