5. Графический метод решения задач линейного программирования.

5.1. Выпуклые множества

Множество М называют выпуклым, если для любых двух точек этого множества отрезок прямой, соединяющий эти точки, целиком лежит в М.

Примерами выпуклых множеств являются круги, эллипсы, многие многоугольники (см. рис 1 и рис. 2). Пример невыпуклого множества изображен на рис. 3.

Рис. 1

Рис. 3

Рис. 2

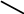
Примерами выпуклых множеств в пространстве являются шар, параллелепипед.

Имеет место следующее важное свойство выпуклых множеств.

Пересечение любого числа выпуклых множеств является выпуклым множеством.

Действительно, так как все множества выпуклые, то все они вместе с двумя точками содержат и отрезки, соединяющие эти точки, а поэтому и пересечение этих множеств будет содержать эти отрезки.

Внутренней точкой множества называют такие точки этого множества, которые имеют некоторую окрестность, целиком лежащую в данном множестве.

Граничной точкой множества называют такие точки , у которых в любой окрестности имеются точки, не принадлежащие данному множеству.

Особый интерес в задачах линейного программирования представляют угловые точки – граничные точки, не являющиеся внутренними ни для какого отрезка, целиком лежащего во множестве.

При пересечении двух прямых под углом мы получим одну угловую точку(Рис.4). Отметим, что если граница выпуклого множества – кривая, то каждая точка этой кривой является граничной (Рис. 5).

Рис.4 Рис. 5

Поэтому, если выпуклое множество ограничено отрезками прямых – оно имеет конечное число угловых точек, в противном случае – бесконечное число угловых точек.

Выпуклое множество, имеющее конечное число угловых точек называют выпуклым многогранником, если оно ограничено, и многогранной областью, если оно неограниченно.

Множество называют замкнутым , если оно содержит все свои граничные точки.

5.2 Геометрический смысл решений систем неравенств.

Как известно, уравнение

С (1)

на плоскости задает прямую. Если мы будем менять значение параметра С, то будем получать прямую, параллельную данной. Из (1) видно, что на данной прямой функция f= будет принимать только одно значение С.

Рассмотрим неравенство

С (2)

Множеством точек (х₁, х₂), удовлетворяющих неравенству (2),будет являться одна из полуплоскостей на которые прямая (1) разбивает всю плоскость( вторая полуплоскость определяется неравенством С ). Если неравенство нестрогое, то прямая (1) будет входить в рассматриваемую полуплоскость, если же неравенство строгое – не будет. Прямая (1) является множеством граничных точек рассматриваемой полуплоскости.

Для того, чтобы определить, какая из двух полуплоскостей удовлетворяет неравенству (2), проще всего взять какую-нибудь контрольную точку Р, не лежащую на границе (1), и подставить ее координаты в (2). Если при этом получается верное неравенство, то полуплоскость, содержащая Р, будет решением (2), в противном случае решением неравенства (2)будет вторая часть плоскости, не содержащая Р. Чаще всего в качестве контрольной точки берется начало координат.

Множеством решений системы неравенств

(3)

будут являться точки, координаты которых удовлетворяют одновременно и одному и другому неравенствам, а поэтому будет являться пересечением полуплоскостей, определяемых данными неравенствами.

Пример. Найти множество решений системы неравенств

		у
	М
						х

Рис 4.

Аналогично, множество решений системы, состоящей из нескольких неравенств, будет получаться при пересечении полуплоскостей, определяемых каждым неравенством системы. Отметим, что полученное множество является выпуклым, так как полуплоскость – выпуклое множество и замкнутым.

При этом могут быть различные случаи:

1. множество решений есть выпуклый многогранник (множество решений ограничено)- рис.5;

2. множество решений неограниченно - рис.6;

3. множество решений единственно - рис. 7;

4. решений нет (множество пересечений пусто). В этом случае говорят, что система неравенств несовместна - рис.8.

Рис.5 Рис.6 Рис. 7 Рис.8

Так как , а значит не равны нулю хотя бы для некоторых i, то функция f не имеет стационарных и критических точек. Это значит, что функция f может принимать наибольшее и наименьшее значение только на границе области.