8.4. Метод множителей Лагранжа.

Одним из методов, позволяющих решить задачу нелинейного программирования, является метод множителей Лагранжа.

Пусть мы имеем задачу:

f( (9)

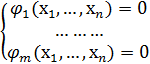(10)

Метод Лагранжа заключается в следующем. Рассмотрим вспомогательную функцию

F( =f( , (11)

где - неизвестные пока множители Лагранжа. Заметим, что если ( удовлетворяют ограничениям (10), то F( , а значит у этих функций совпадают и экстремумы.

Запишем необходимые условия экстремума для функции F( :

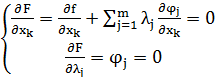, (12)

k=1,…,n, j=1,…,m.

Очевидно, любая точка ( удовлетворяющая условиям (12), будет удовлетворять и условиям (10), поэтому найденный экстремум функции F будет также являться и экстремумом функции f.

Нужно отметить, что полученные точки являются точками локального экстремума и для нахождения точек глобального экстремума функции f нужны дополнительные исследования.

Пример. Некоторый товар со склада могут реализовывать две фирмы. Накладные расходы при реализации продукции первой фирмой х единиц товара составляют х², а накладные расходы при реализации второй фирмой у единиц товара составляют 2у².

Определить, какое количество товара нужно выделить каждой фирме, чтобы накладные расходы были минимальны, если общее число единиц товара 1200.

Составим математическую модель задачи.

f= (13)

х+у=1200. (14)

Составим вспомогательную функцию

F= (15)

Необходимые условия экстремума (15)

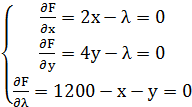(16)

Из первых двух уравнений системы (16) и =4у, откуда 2х=4у или х=2у.

Тогда, из третьего уравнения (16)

1200 – 2у – у =0 или у=400, х=800, f(800, 400)=960 000.

Покажем, что точка (800, 400) – точка минимума функции f.

Возьмем х=900, тогда из (14) у=300, f(900, 300)=990 000, возьмем х=700, тогда из (14) у=500, f(700, 500)=990 000. Поэтому, f=960 000 – наименьшее значение функции.

9. Элементы теории игр.

9.1.Основные понятия теории игр

До сих пор мы рассматривали ситуации. Когда имелось одно лицо, которое принимало решение таким образом, чтобы максимизировать (минимизировать) критерий качества. Однако часто встречаются ситуации, когда имеется группа лиц, имеющих различные интересы. Например, в экономике несколько фирм, выпускающих одинаковую продукцию, имеют цель получить максимальную прибыль(при этом естественно их конкуренты должны будут получать минимум прибыли). Такими задачами занимается раздел математики, который называется теорией игр.

Теорией игр называют математическую дисциплину, исследующую такие задачи, в которых принятие решения зависит от нескольких участников.

Под игрой мы будем понимать математическую модель, описывающую действия нескольких участников.

Мы будем рассматривать игры, в которых имеются два игрока, преследующие диаметрально противоположные цели. Кроме того, будем считать, что игры имеют нулевую сумму выигрыша (то есть выигрыш одного игрока равен проигрышу второго).

Варианты действия игроков называют стратегиями.

Пусть первый игрок имеет стратегии А₁,…,А_n, а второй игрок имеет стратегии В₁,…,В_m . Пусть а_ij – выигрыш первого игрока (проигрыш второго игрока), при применении первым игроком стратегии А_i, а вторым – В_j. Выигрыши первого игрока (проигрыши второго), соответствующие различным стратегиям, удобно записать в виде матрицы, которую называют платежной матрицей

.

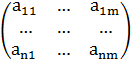В данной матрице строки соответствуют различным стратегиям первого игрока, а столбцы – различным стратегиям второго игрока. Такие игры называют матричными играми.

Рассмотрим следующую игру. Два игрока имеют карточки с цифрами 1, 2, 3, 4. Одновременно они открывают по одной карточке. Если сумма цифр на карточках четная, то первый игрок получает выигрыш, равный сумме этих цифр. Если сумма цифр нечетна, то выигрыш получает второй игрок. Платежная матрица будет иметь вид

В₁ В₂ В₃ В₄

А=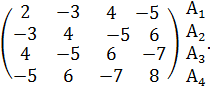

Если первый игрок выберет стратегию А₁, то второму игроку выгоднее всего выбрать стратегию В₄, так как его проигрыш будет минимален (-5),

-5= .

Если первый игрок выберет стратегию А₂. То второму игроку выгоднее всего выбрать стратегию В₃. В этом случае

=-5.

Аналогично, для А₃ , для А₄ .

Наибольшее из полученных значений =-5, то есть

Эта величина определяет тот минимальный выигрыш, который может гарантировать себе первый игрок. Величину

называют нижней ценой игры или максиминным гарантированным выигрышем.

Рассуждаем теперь с позиций второго игрока (в таблице записан его проигрыш, поэтому он стремится сделать его как можно меньше). Если он применит стратегию В₁. то его наибольший проигрыш , для стратегии В₂ , для стратегии В₃ , для стратегии В₄ . Из всех этих значений наименьший проигрыш второго игрока

.

Величину

называют верхней ценой игры или минимаксным гарантированным проигрышем второго игрока.

Можно показать, что .

Пример. Швейная фабрика готовится к выпуску осеннего костюма, причем имеются три его варианта А₁, А₂, и А₃. Спрос на каждый из вариантов может зависеть от того, какой будут осень (теплая(Т), средняя(С) и холодная(Х)). Каждый из вариантов костюма требует своих затрат и приносит различную прибыль. Прибыль, которую получит предприятие в зависимости от варианта костюма и от погодных условий, приводится в таблице

	Т	С	Х
А1	25	25	25	25
А2	24	26	26	24
А3	23	24	27	23
	25	26	27

Очевидно,

= =25.

Такие игры, у которых называют играми с седловой точкой. Для таких игр существует стратегия, которая для одного игрока дает наибольший выигрыш, а для другого наименьший проигрыш.

Стратегия оптимальна для обеих игроков и отклонение от нее для первого игрока уменьшит выигрыш, а для второго игрока увеличит проигрыш.

Число называют ценой игры.

В том случае, если игра не имеет седловой точки, вводится понятие смешанной стратегии. В этом случае мы рассматриваем игру не однократно, а много раз, при этом стратегии каждый раз выбираются случайно с некоторой вероятностью. Такие стратегии называют смешанными стратегиями (в отличии от них стратегии, используемые постоянно, называют чистыми стратегиями).

Рассмотрим простейшую игру 2Х2 с платежной матрицей

Пусть игра состоялась n раз, причем первый игрок применил m раз стратегию А₁ и (m-n) раз стратегию А₂, а второй игрок применял чистую стратегию В₁. Тогда выигрыш первого игрока за n игр , а средний выигрыш первого игрока за одну игру

.

Обозначив х₁= - вероятность применения первым игроком стратегии А₁ и через х₂= - вероятность применения первым игроком стратегии А₂, получим средний выигрыш первого игрока х₁ +х₂ .

Если второй игрок применяет чистую стратегию В₂, то средний выигрыш первого игрока за одну игру будет равен х₁ +х₂ .

Пару чисел (х₁, х₂) называют смешанной стратегией первого игрока. Очевидно, х₁+х₂=1.

Аналогично, если второй игрок применяет стратегию В₁ с вероятностью у₁, а стратегию В₂ с вероятностью у₂, то смешанной стратегией второго игрока называют пару чисел (у₁, у₂).

Американский математик Джон фон Нейман доказал

Теорема 1. Всякая матричная игра с нулевой суммой имеет решение, хотя бы в смешанных стратегиях .

(без доказательства).

О том как можно решить матричную игру говорит следующая

Теорема 2. Если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш равен цене игры , не зависимо от того с какими вероятностями будет применять другой игрок свои стратегии, вошедшие в оптимальную (возможно даже чистые стратегии).

(без доказательства).

Пример. Найти решение игры, заданной платежной матрицей

Так как , а , то данная игра не имеет седловой точки и 2 . Поэтому оптимальными стратегиями в этой игре будут смешанные стратегии.

Пусть х₁- вероятность, с которой первый игрок применяет стратегию А₁, а х₂ – стратегию А₂ Тогда, если второй игрок применяет чистую стратегию В₁, то по теореме 2

х₁+4х₂= .

Если второй игрок применяет чистую стратегию В₂, то

3х₁+2х₂= .

Кроме того, х₁+х₂=1.

Таким образом, получаем систему трех уравнений с тремя неизвестными

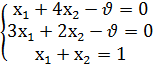
Решая эту систему, получим х₁=0,5, х₂=0,5, =2,5.

Составим систему уравнений для второго игрока, обозначая у₁- вероятность применения стратегии В₁, а у₂ – стратегии В₂.

Решая систему, получим у₁=0,25, у₂=0,75.

При решении матричных игр иногда удается упростить задачу, отбрасывая заведомо невыгодные стратегии для первого и второго игроков. Пусть имеем платежную матрицу

.

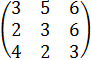Для первого игрока невыгодной будет стратегия А₂ по сравнению со стратегией А₁ (вторая строка матрицы по сравнению с первой), так как при любой стратегии второго игрока выигрыши первого игрока при стратегии А₁ не меньше, чем при А₂.

Поэтому платежную матрицу можно записать в виде

.

Для второго игрока стратегия В₃ будет невыгодной по сравнению с В₂, так как проигрыши второго игрока в В₃ больше при любой стратегии первого игрока. Поэтому платежную матрицу можно еще упростить