
- •1. Понятие модели.
- •1.1. Модели и моделирование. Классификация моделей
- •В настоящее время для постижения истины существует 3 пути:
- •1.2. Классификация моделей
- •1.3. Адекватность моделей
- •2. Математические модели и методы их расчета
- •2.1. Математические модели.
- •2.1. Понятие операционного исследования
- •2.3. Этапы построения математических моделей
- •Можно выделить следующие основные этапы построения математической модели:
- •2.4 Математические оптимизационные модели.
- •2.4. Необходимые сведения из матричной алгебры
- •2.5. Системы линейных алгебраических уравнений
- •2.5. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
- •3. Простейшие оптимизационные задачи.
- •3.1. Экстремумы функции одной переменной.
- •Экстремумы функции нескольких переменных.
- •4. Математические модели экономических задач.
- •4.1. Транспортная задача
- •4.2 Задача об использовании ресурсов.
- •4.3. Задача о диете.
- •4.4. Общая формулировка задачи линейного программирования
- •Стандартная задача линейного программирования.
- •Каноническая задача линейного программирования.
- •Общая задача линейного программирования.
- •5. Графический метод решения задач линейного программирования.
- •5.1. Выпуклые множества
- •5.2 Геометрический смысл решений систем неравенств.
- •5.3. Графический метод решения задач линейного программирования. Пример.
- •5.4. Геометрический метод решения задачи. Общий случай.
- •6.Симплекс-метод решения задачи линейного программирования.
- •6.1. Выпуклые многогранники.
- •6.2.Симплекс-метод. Пример.
- •6.3.Симплекс метод. Общий случай.
- •Симплекс-таблицы. Пример.
- •7.Двойственность в линейном программировании.
- •7.1. Двойственные задачи линейного программирования.
- •7.2. Теоремы двойственности..
- •7.3. Анализ чувствительности задачи линейного программирования..
- •Решение транспортной задачи.
- •7.1 Особенности транспортной задачи.
- •7.2. Опорный план транспортной задачи
- •7.3. Метод потенциалов.
- •8.Задачи нелинейного программирования.
- •8.1. Общая постановка задачи нелинейного программирования.
- •8.2. Задачи нелинейного программирования с линейной целевой функцией и нелинейными ограничениями.
- •8.3. Задачи нелинейного программирования с нелинейной целевой функцией и линейными ограничениями.
- •8.4. Метод множителей Лагранжа.
- •Элементы теории игр.
- •9.1.Основные понятия теории игр
- •8.3. Сведение матричной игры к задаче линейного программирования.
2.5. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
Цель балансового анализа: ответить на вопрос –каким должен быть объем производства каждой из n отраслей, чтобы полностью удовлетворить спрос в продукции этой отрасли. При этом каждая отрасль является также и потребителем и своей продукции и продукции других отраслей. Математическая модель многоотраслевой экономики была разработана в 1936 г. Американским экономистом В.Леонтьевым.
Пусть имеем n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственные нужды данной отрасли и других отраслей промышленности, а оставшаяся часть идет на личное и общественное (непроизводственное) потребление. Введем обозначения:
![]() -
общий (валовый) продукт i
отрасли i
=1,…, n;
-
общий (валовый) продукт i
отрасли i
=1,…, n;
![]() -
объем продукции i
отрасли, потребляемый j
отраслью j=1,…,
n;
-
объем продукции i
отрасли, потребляемый j
отраслью j=1,…,
n;
![]() - объем конечного продукта для
непроизводственного потребления.
- объем конечного продукта для
непроизводственного потребления.
Тогда
![]() (i=1,…, n).
(5)
(i=1,…, n).
(5)
Уравнения (1) называют соотношениями баланса.
Введем коэффициенты прямых затрат
![]() ,
,
которые показывают затраты продукции i отрасли на производство единицы продукции j отрасли.
Можно считать, что в течение какого-то времени эта величина будет постоянной.,. определяемой сложившейся технологией производства. Тогда
![]() (i,
j=1,…,
n)
(i,
j=1,…,
n)
и соотношения баланса (5) примут вид
![]() (i=1,…, n). (6)
(i=1,…, n). (6)
Обозначим
Х=![]() ,
Y=
,
Y=![]() ,
A=
,
A=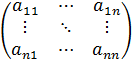 ,
тогда (6) можно записать в виде
,
тогда (6) можно записать в виде
X=AX+Y (7)
Основная
задача межотраслевого баланса
: найти
такие X=(![]() ,
чтобы по известной матрице А обеспечить
заданные величины
,
чтобы по известной матрице А обеспечить
заданные величины ![]()
Запишем (7) в виде
(Е-А)Х=Y или
Х=(Е-А)-1 Y
Матрица S=(Е-А)-1 называется матрицей полных затрат.
Задача 2.3 Данные об исполнении баланса ( в усл. ед) за предыдущий год даны в таблице
Отрасль |
Производство |
Валовый выпуск прош |
Конечн. продукт след. |
|
Металлургия |
Машиностроение |
|||
Металлургия |
10 |
20 |
100 |
150 |
Машиностроение |
30 |
40 |
200 |
200 |
Требуется найти объем валового выпуска, чтобы обеспечить объем конечного продукта на следующий год. Обозначим, х1=100, х2=200, х11=10, х12=20, х21=30, х22=40, у1=150, у2=200. Х1, Х2 –валовой выпуск, требуемый на следующий год.
Найдем
![]() =
=![]() =0,1,
=0,1,
![]() =
=![]() =0,1,
=0,1,
![]() =
=![]() =0,3
=0,3
![]() =
=![]() =0,2
=0,2
Поэтому
А=![]() , S=E-A=
, S=E-A=![]() .
Det
S =0,69.
.
Det
S =0,69.
ST
=![]() .
А11=0,8,
А12=0,1,
А21=0,3,
А22=0,9.
.
А11=0,8,
А12=0,1,
А21=0,3,
А22=0,9.
S-1=![]() ,
а
,
а ![]() =S-1
Y=
=S-1
Y=![]() =
= ![]() .
.
3. Простейшие оптимизационные задачи.
3.1. Экстремумы функции одной переменной.
Необходимое и достаточное условие экстремума функции одной переменной.
Пусть дана дважды
непрерывно дифференцируемая
функция
f
одной переменной , где x![]() .
.
Определение 1. Точка х называется точкой локального минимума (максимума) функции, если найдется некоторая окрестность этой точки, для всех точек х которой выполняется условие:
f(x )>f(x) (f(xo)< f(x)).
Определение 2. Точки локального максимума и минимума называются точками экстремума функции f.
Данные определения имеют место и для функций нескольких переменных, только в этом случае х и х0 являются векторами, х=(х1,…, хn), x n.
Определение 3. Точки, в которых производная f’ равна нулю или не существует, называются критическими.
Определение 4. Точки, в которых производная f’равна нулю, называются стационарными.
Теорема 1. (Необходимый признак экстремума функции.) Если точка x является точкой экстремума функции, то она является критической точкой.
Теорема 2. (Первый достаточный признак экстремума.) Пусть x - критическая точка Тогда, если при переходе через хо производная f’ меняет знак с «-» на «+»то хо- точка локального минимума. Если же производная f’ меняет знак с «+» на «-»то хо- точка локального максимума.
Теорема 3. (Второй достаточный признак экстремума.) Если в стационарной точке f”(x )<0, то x - точка локального максимума, если f”(x )>0то x - точка локального минимума.
Если критическая точка одна, то если это будет точка локального максимума (минимума) – она будут являться точкой наибольшего наименьшего) значения функции.
Наибольшее и наименьшее значение функции на отрезке.
Пусть дана дважды
непрерывно дифференцируемая
функция
f
одной переменной , где x![]() .
.
Для нахождения наибольшего и наименьшего значения функции применяют следующий алгоритм:
Находим критические точки функции, принадлежащие
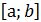 .
Обозначим их х1,…,хn;
.
Обозначим их х1,…,хn;Находим значения f(x1),…,f(xn), а также значения f(a) и f(b);
Среди полученных значений выбираем наибольшее (это будет наибольшее значение функции) и наименьшее (это будет наименьшее значение функции.)
Рассмотрим решение задачи 2.1.
f(х,у)=сху max (1)
2х+2у=L, х>0, у>0 (2)
Выражая
из (2) у=![]() и вводя ограничение
и вводя ограничение ![]() получим задачу: найти наибольшее значение
функции f=с
получим задачу: найти наибольшее значение
функции f=с![]() на отрезке
на отрезке ![]() .
.
Получим f’=0 при х=
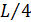 - единственная критическая точка.
- единственная критическая точка.
Находим f(
 ,
f(0)=0,
f(
,
f(0)=0,
f(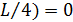 .
.Поэтому х= , у=
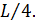
Из равенства в ограничениях (2) мы выразили у через переменную х и свели задачу к нахождению наибольшего значения функции одной переменной.
