
- •1. Понятие модели.
- •1.1. Модели и моделирование. Классификация моделей
- •В настоящее время для постижения истины существует 3 пути:
- •1.2. Классификация моделей
- •1.3. Адекватность моделей
- •2. Математические модели и методы их расчета
- •2.1. Математические модели.
- •2.1. Понятие операционного исследования
- •2.3. Этапы построения математических моделей
- •Можно выделить следующие основные этапы построения математической модели:
- •2.4 Математические оптимизационные модели.
- •2.4. Необходимые сведения из матричной алгебры
- •2.5. Системы линейных алгебраических уравнений
- •2.5. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
- •3. Простейшие оптимизационные задачи.
- •3.1. Экстремумы функции одной переменной.
- •Экстремумы функции нескольких переменных.
- •4. Математические модели экономических задач.
- •4.1. Транспортная задача
- •4.2 Задача об использовании ресурсов.
- •4.3. Задача о диете.
- •4.4. Общая формулировка задачи линейного программирования
- •Стандартная задача линейного программирования.
- •Каноническая задача линейного программирования.
- •Общая задача линейного программирования.
- •5. Графический метод решения задач линейного программирования.
- •5.1. Выпуклые множества
- •5.2 Геометрический смысл решений систем неравенств.
- •5.3. Графический метод решения задач линейного программирования. Пример.
- •5.4. Геометрический метод решения задачи. Общий случай.
- •6.Симплекс-метод решения задачи линейного программирования.
- •6.1. Выпуклые многогранники.
- •6.2.Симплекс-метод. Пример.
- •6.3.Симплекс метод. Общий случай.
- •Симплекс-таблицы. Пример.
- •7.Двойственность в линейном программировании.
- •7.1. Двойственные задачи линейного программирования.
- •7.2. Теоремы двойственности..
- •7.3. Анализ чувствительности задачи линейного программирования..
- •Решение транспортной задачи.
- •7.1 Особенности транспортной задачи.
- •7.2. Опорный план транспортной задачи
- •7.3. Метод потенциалов.
- •8.Задачи нелинейного программирования.
- •8.1. Общая постановка задачи нелинейного программирования.
- •8.2. Задачи нелинейного программирования с линейной целевой функцией и нелинейными ограничениями.
- •8.3. Задачи нелинейного программирования с нелинейной целевой функцией и линейными ограничениями.
- •8.4. Метод множителей Лагранжа.
- •Элементы теории игр.
- •9.1.Основные понятия теории игр
- •8.3. Сведение матричной игры к задаче линейного программирования.
7.2. Теоремы двойственности..
Теорема 1. (Первая теорема двойственности). Если одна из взаимно двойственных задач имеет решение, то его имеет и другая, причем = .
Следствие. Если одна из двойственных задач не имеет решения, то и вторая не имеет решения.
Теорема
2.
(Вторая теорема двойственности). Для
того, чтобы решения (![]() ),
(
),
(![]() )были
оптимальны, необходимо и достаточно
выполнения условий
)были
оптимальны, необходимо и достаточно
выполнения условий
![]() , (7)
, (7)
![]() . (8)
. (8)
Условия (7), (8) называют условиями дополняющей нежесткости. Используя эти условия, из решений одной из двойственных задач можно найти решения другой задачи.
Пример 1. Пусть имеем исходную задачу распределения ресурсов:
Пусть для производства трех видов товаров Т1 , Т2 и Т3 требуются ресурсы Р1 и Р2. Наличие ресурсов, и их нормы расхода, требуемые на производство единицы товара, и прибыль предприятия при реализации единицы товара приводятся в таблице.
|
Т1 |
Т2 |
Т3 |
Имеющиеся ресурсы |
Р1 |
3 |
1 |
1 |
b1= 5 |
Р2 |
1 |
1 |
3 |
b2= 3 |
Прибыль от реализации |
6 |
4 |
6 |
|
Требуется составить такой план работы предприятия, чтобы при этом получить максимальную прибыль.
Обозначим через х1, х2, х3 соответственно количество товара Т1 , Т2 и Т3. Тогда математическая модель задачи имеет вид:
![]() (9)
(9)
х1≥0,
х2≥0,
х3![]()
F=![]()
Составим задачу, двойственную задаче (9), (10).
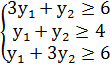 (11)
(11)
y1≥0,y2≥0
Z=![]() (12)
(12)
которую можно решить графически.
у2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у1 |
![]() .
.
Тогда, согласно первой теореме двойственности = =14.
Оптимальные
![]() найдем из условий (7)-(8)
найдем из условий (7)-(8)
1![]()
![]() ,
,
3![]() = 0,
= 0,
![]() ,
,
![]() ,
,
![]() ,
,
откуда получаем

и
решения задачи (9)-(10) ![]() =14.
=14.
Рассмотрим связь между двойственными задачами линейного программирования в каноническом виде на примере 1.Сведем ограничения (9) к ограничениям вида равенств
![]()
а ограничения (11)
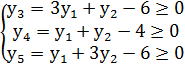
Тогда получим задачи
Исходная задача
х1≥0, х2≥0, х3 F= |
Двойственная задача
y1≥0,y2≥0, Z= |
Рассмотрим
решения этих задач (см. пример 1): исходной:
![]()
![]()
![]() двойственной
:
двойственной
:![]()
![]()
Кроме
того, из системы уравнений (14) получим
![]() =0 и
=0 и ![]() =4
=4
![]()
![]() .
.
Установим соответствие между первоначальными и дополнительными переменными
Переменные исходной задачи |
||||
Первоначальные |
Дополнительные |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополнительные |
Первоначальные |
|||
Переменные двойственной задачи |
||||
Мы видим, что нулевым компонентам исходной задачи соответствуют ненулевые компоненты двойственной задачи, а ненулевым компонентам исходной задачи соответствуют нулевые компоненты двойственной задачи и наоборот.
Имеет место следующая теорема, которую также называют второй теоремой двойственности.
Теорема 2’. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, то есть для любых i=1,…,m, j=1,…,n :
если




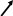
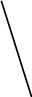




 (14)
(14)