Порядок выполнения работы

1. Из табл. 3 приложения студенту необходимо выписать исходные данные в соответствии с вариантом, выданным преподавателем.

В задании использовано малое количество исходных данных в связи с тем, что необходимо для их обработки применить большое количество вычислений.

В результате сбора и обработки информации о надежности гидромотора при эксплуатации получены значения наработки изделия на отказ. Требуется проверить гипотезу о том, что выборка принадлежит нормально распределенной генеральной совокупности.

Таблица 47

Результаты вычислений по критерию ω²

Номер наблюдения	(2j-1)/2n	F(xj)	Ln F(xj)	((2j-1)/2n)Ln F(xj)	1-(2j-1)/2n	1-F(xj)	Ln[1-F(x j)]	(1-(2j-1)/2n) Ln[1-F(x j)]	((2j-1)/2n) Ln F(xj)+ +(1-(2j-1)/2n) Ln[1-F(xj)]
1	2	3	4	5	6	7	8	9	10
.
.
.

Необходимо оценить параметры нормального распределения, вычисленные по исходным данным, для этого необходимо заполнить табл. 43 лабораторной работы № 13. по данным табл. 43 строят графики функции теоретического и опытного распределений.

2. На основании рассчитанной табл. 43 заполняют табл. 47, а графу 3 – восьмой графой из табл. 43.

3. Вычисления по критерию ω² проводят в следующем порядке:

определяют значение величины :

(135)

где x_j (j = 1, 2, …, n) – результат наблюдений, имеющий j-й номер в вариационном ряду .

При вычислении по формуле (135) рекомендуется пользоваться табл. 47. В табл. 47 рекомендуется проводить вычисления с точностью до 5 значащих цифр, округляя окончательный результат вычислений по формуле (135) до двух значащих цифр.

4. После заполнения табл. 47 необходимо просуммировать значения, занесенные в десятую графу.

Значения величины получают по формуле (135), которую в нашем случае можно переписать:

(136)

где (136) – сумма десятой графы.

5. Далее в табл. 4 приложения находят значения функции а, соответствующее вычисленному значению . Функция а представляет собой функцию распределения величины .

6. Задают уровень значимости а. Рекомендуется выбирать значение а, равное 0,1 или 0,2.

Если а ≥ (1-а), то гипотезу о согласии эмпирического и теоретического распределения отвергают, если а < (1-а), то гипотезу принимают.

7. Построить графики функций теоретического и опытного распределения. Сделать вывод о принятии или непринятии гипотезы о согласии наработки гидромотора с нормальным распределением.

8. Отчет защитить у преподавателя.

Контрольные вопросы

1. Как построить график теоретической функции распределения?

2. Как построить график эмпирической функции распределения?

3. Когда применяют критерий ω²?

Лабораторная работа № 16

Построение и применение вероятностных сеток для логарифмически нормального распределения (без сдвига)

Ц е л ь р а б о т ы: построить вероятностную сетку для логарифмически нормального распределения (без сдвига), на которой интегральная функция распределения будет иметь вид прямой.

Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.

Основные теоретические сведения

Для каждого закона распределения можно построить вероятностную сетку, на которой интегральная функция распределения будет иметь вид прямой.

При наличии таких вероятностных сеток можно с достаточной для практики точностью определять следующие статические характеристики распределения значений показателя надежности: вид закона распределения значений показателя, математической ожидание, среднее квадратическое отклонение, коэффициент вероятности, вероятность безотказной работы или возникновение отказа за заданную наработку и т.д.

Вероятностная сетка (или вероятностная бумага) для данного распределения вероятностей представляет собой прямоугольную сетку, на которой масштаб выбран таким образом, чтобы график функции этого распределения, построенный на сетке, представлял собой прямую линию.

Если имеется выборка объемом n из значений случайной величины х, то на вероятностную сетку для данного вида распределения наносят точки графика F_э – эмпирической функции распределения.

Затем проводят прямую так, чтобы нанесенные точки отклонялись от нее как можно меньше. Эту прямую обычно строят визуально.

Одновременно с определением оценок параметров можно производить графическую проверку согласия эмпирического распределения с теоретическим.

Если нанесенные эмпирические точки мало отклоняются от проведенной прямой, то это свидетельствует о том, что опытные данные не противоречат тому виду распределения, для которого построена сетка. При проведении этой проверки надо учитывать, что при приближении к концам выборки опытные точки могут больше отклоняться от прямой, чем в средней части графика.

Оценки параметров распределения находят по углу наклона построенной прямой и по отрезкам, отсекаемым ею на осях координат (с учетом масштаба).

Для проведения анализа информации о надежности графо-аналитическим методом необходимо обработать результаты наблюдений.

Рассмотрим построение эмпирической функции распределения.

В случае, если объем выборки не превосходит 50, элементы выборки нумеруют в порядке возрастания:

Эмпирическую функцию распределения F_э(х) рекомендуется определять по формуле:

(137)

или

(138)

Формулу выбирают из соображений удобства вычислений.

Если два или более элемента выборки совпадают, т.е. x_i = x_i+1 = … = = x_i+l < x_i+l+1, то F_э(х) в этих точках считают равной F_э(х_i+l), где F_э(х_i+l) определяют по формуле (137) или по формуле (138) с заменой i на i + l.

Если n > 50, группируют данные. Для этого наибольшее и наименьшее значения показателя в выборке обозначают соответственно через x_min и x_max, а затем выбирают числа х^* и х^** с условием, что х^* ≤ x_min, х^** ≥ x_max. Ряд значений показателя [х^*, х^**] разбивают на k равных интервалов, число точек в j-м интервале (j = l,…, k) обозначают m_j. При этом должны выполняться неравенства 10 ≤ k ≤ 20, m_j ≥ 5 (j = 1,…, k). Из точки на границе интервалов в смежные интервалы относят по ½ точки. Значение интервала определяют по формуле:

(139)

где k – предполагаемое число интервалов.

Полученное значение интервала округляют до целого числа, а затем подсчитывают число значений показателя в каждом интервале (частоты).

После группировки определяют эмпирическую функцию распределения при j = 1, 2,…, k по формуле:

(140)

j = 1, 2,…, k.

Полученные значения эмпирической функции наносят на вероятностную сетку одного из законов распределения.

Логарифмически нормальное распределение (без сдвига)

Положительная случайная величина y имеет логарифмически нормальное распределение, если ее логарифм х распределен нормально.

На практике применяются два варианта:

при этом имеет место соотношение:

где М – коэффициент перехода от натуральных к десятичным логарифмам, равный 0,4343.

Плотности вероятности распределения имеют вид:

Существует такое значение y₀, для которого:

Тогда для плотности вероятности распределения величины y:

Для функции распределения:

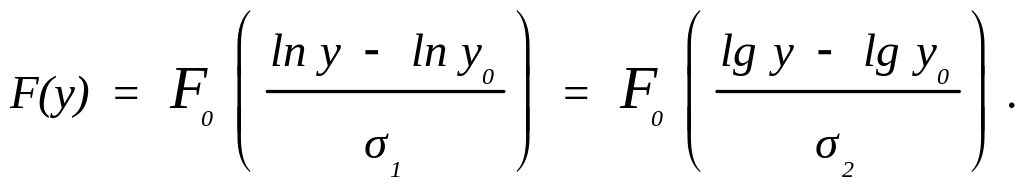
Если y – наработка изделия до отказа, то вероятность безотказной работы изделия на протяжении наработки y находится по уравнению:

или, что то же самое:

Вероятностная сетка для логарифмически нормального распределения устроена следующим образом.

По оси абсцисс применяют логарифмическую шкалу, а на оси ординат откладывают значения y и надписывают величину F₀(y), где F₀(y) – значение нормированной центрированной функции логарифмически нормального распределения.

Величина:

(141)

где k_x – коэффициент масштаба по оси абсцисс, равный:

(142)

где L – ширина графика; x_max, x_min – наибольший и наименьший элементы выборки соответственно.

Значение величины L следует выбирать так, чтобы значение коэффициента k_x, вычисленное по формуле (142), было удобно для расчетов. Рекомендуется выбирать наибольшее из возможных значений L.

Для k_x = 100 значения S_x(x) приведены в табл. 10.4 [15].

Величину S_у(F) определяют при помощи равенства:

, (143)

где Н – длина шкалы по оси ординат, мм.

В табл. 10.1 [15] приведены значения S_у(F) для случая Н = 300 мм.

Если известно, что случайная величина имеет логарифмически нормальное распределение без сдвига, то на вероятностную сетку для логарифмически нормального распределения наносят точки при помощи формул (141) и (143). После этого строят прямую.

Если А – точка пересечения прямой с осью абсцисс, а точка О – начало координат, то оценку параметра а вычисляют по формуле:

(144)

где k_x – коэффициент масштаба.

Оценку а можно определить по табл. 10.4. [15]:

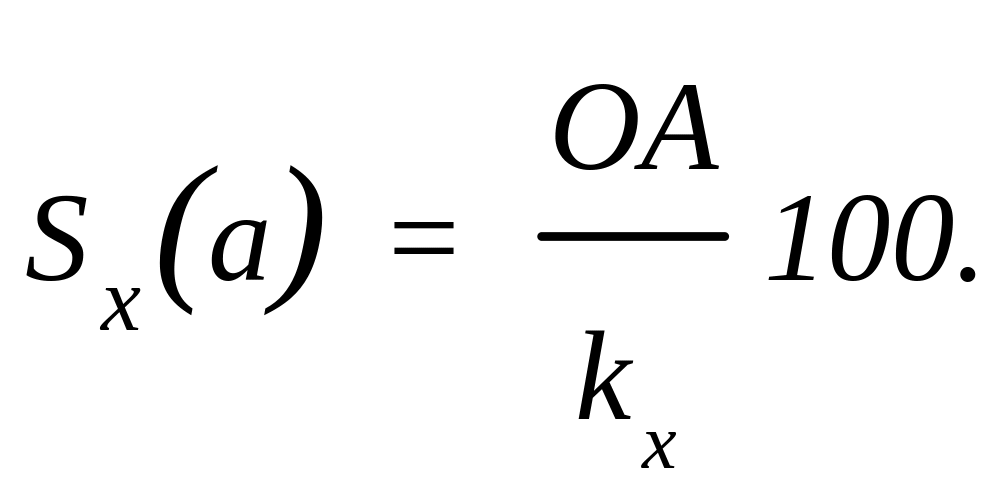(145)

Оценка параметра σ:

где g – угловой коэффициент прямой, равный:

. (146)

Здесь β – угол наклона прямой к оси абсцисс, при Н = 300 мм.

(147)