Лекция №12 Функциональные последовательности и ряды (продолжение)

Нас будут интересовать следующие три задачи.

Задача 1. Пусть последовательность функций . Когда .

Пример. Пусть .

Аналогичную задачу можно поставить и для функционального ряда.

П ример. .

Задача 2. Пусть (R – интегрируема). Когда можно гарантировать, что или .

.

Задача 3. Пусть (С¹- непрерывно дифференцируема). Когда , или .

Пример. .

Предельная функция не наследует хорошие свойства функции последовательности.

2. Равномерная сходимость последовательности функций и функционального ряда

Вначале проанализируем условие поточечной сходимости последовательности функций на отрезке: на .

равномерно сходится на к f(x), т.е. , если .

Пусть , тогда эквивалентное определение равномерной сходимости выглядит так: .

Из равномерной сходимости вытекает поточечная сходимость, а обратное - неверно. Рассмотрим примеры.

Пример 1.

, т.е. поточечная сходимость есть, а равномерной сходимости нет.

Пример 2.

т.е. равномерной сходимости нет.

Пример 3.

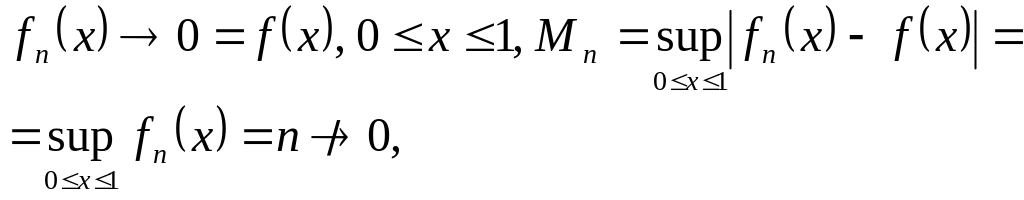
т.е. равномерной сходимости нет.

Пример 4.

т.е. равномерная сходимость есть, но и в этом случае её недостаточно.

Критерий Коши. , или с другой стороны . Критерий Коши также называется равномерной фундаментальностью.

Доказательство. Необходимость.

Пусть , тогда

равномерная фундаментальность последовательности f_n(x).

Достаточность.

Пусть f_n(x) – равномерная фундаментальная последовательность  f_n(x) – фундаментальная (по критерию Коши) . Запишем подробно условие равномерной фундаментальности:

.

Доказано.

Лекция №13 Функциональные последовательности и ряды (продолжение)

Ряд называется равномерно сходящимся к своей сумма на [a, b], если его последовательность частичных сумм сходится равномерно на [a, b] к S(x), т.е. или .

Для функционального ряда критерий Коши выглядит так: равномерно сходится на [a, b] тогда и только тогда, когда последовательность частичных сумм S_n(x) равномерно фундаментальная на [a, b], т.е. .

Пример.

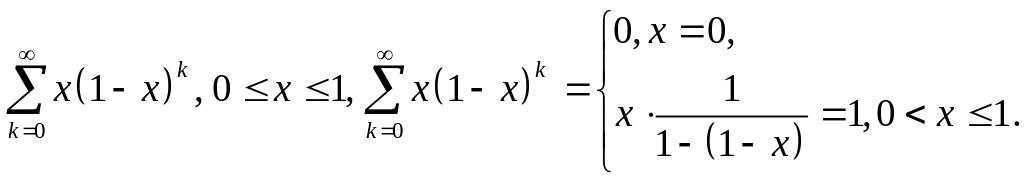
Применим критерий Коши:

равномерной сходимости нет.

Для равномерной сходимости функционального ряда можно указать некоторые достаточные признаки.

1. Признак Вейерштрасса.

Если сходится, то сходится равномерно на [a, b].

Доказательство. Будем использовать критерий Коши для равномерной сходимости функционального ряда.

(по критерию Коши)

Доказано.

Пример.

Можно показать, что всюду сходящийся ряд, тем не менее, на периоде не является равномерно сходящимся. Тем не менее, для ряда справедливо следующее важное утверждение: частичные суммы ряда равномерно ограничены для любого х:

Доказательство. В силу периодичности и нечётности достаточно рассмотреть

Для оценки воспользуемся преобразованием Абеля:

Далее:

Итак,

Сформулируем признаки равномерной сходимости Дирихле и Абеля для рядов вида: (1).

2. Признак Дирихле.

Если для ряда (1) выполнены условия:

1. 

2. 

3. 

то ряд (1) сходится равномерно на [a, b].

3. Признак Абеля.

Если для ряда (1) выполнены условия:

1. 

2. 

3. то ряд (1) сходится равномерно на

Эти признаки доказываются точно также как и для числовых рядов, используя преобразование Абеля и критерий Коши для сходящихся рядов.

Задача. При каких условиях (неубывающая)

Достаточные условия вытекают из признака Дирихле:

Остаётся проанализировать условия (1) и (2) и потребовать, чтобы Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.