Лекция №18 Ряды Фурье

1. Отдельные точки Евклидова пространства интегрируемости функций, ортогональные системы в нём.

Пусть линейное пространство интегрируемых по Риману на отрезке [a, b] функций. В нём можно определить скалярное произведение: удовлетворяющее следующим аксиомам скалярного произведения:

1. (нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).

2. 

3. 

4. 

Линейное пространство со скалярным произведением называется Евклидовым пространством. Евклидово пространство можно рассматривать как нормированное, в котором норма определяется по правилам: 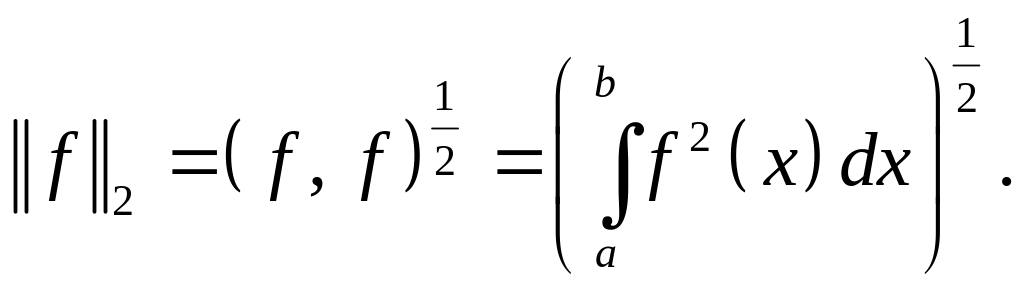Для такого отображения выполнены все аксиомы нормы:

1. 

2. 

3. неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского

В свою очередь неравенство Коши-Буняковского позволяет определить и угол между функциями: 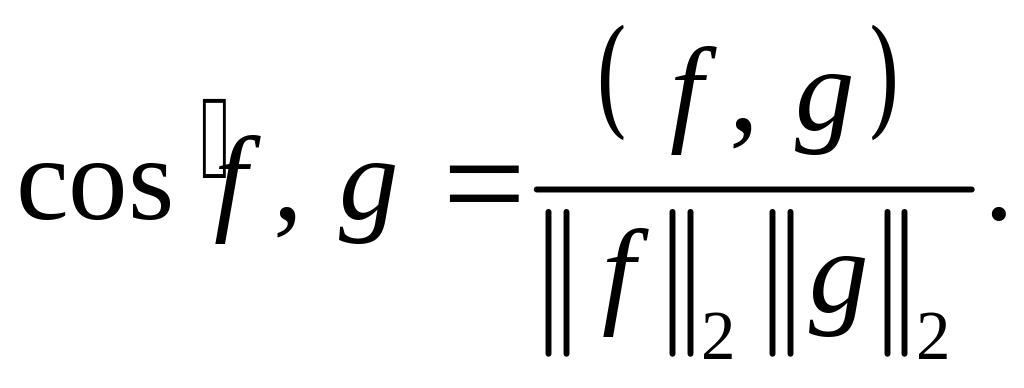В частности Норма позволяет определить расстояние между функциями и сходимость последовательности функций: Такую сходимость называют среднеквадратичной сходимостью

Сравним равномерную сходимость и среднеквадратичную сходимости на отрезке [a, b]; из равномерной сходимости вытекает среднеквадратичная сходимость:

Обратное неверно.

равномерной сходимости нет.

Пространство является бесконечномерным. В нём линейно-независимую систему, например, образуют функции (система степеней).

Задача. Охарактеризовать мощность пространства

Счётная система функций называется ортогональной, если и ортонормированное, если система ортогональная и нормированная, т.е. . Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.

3. Задача о наилучшем среднеквадратичном приближении функции по ОНС.

Пусть ОНС. Линейные комбинации вида будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство размерности п, т.е. , с базисом

Задача. Доказать, что ОНС – линейно-независимая система.

Для величина называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином называется полиномом наилучшего среднеквадратичного приближения.

Лекция №19 Ряды Фурье (продолжение)

Теорема. причём

Доказательство. ОНС,

Итак, единственен.

Доказано.

Если ОНС, то функциональный ряд называется рядом Фурье функции f по ортогональной системе а коэффициенты этого ряда называются коэффициентами Фурье.

Частичные суммы ряда Фурье обладают экстремальным свойством: они являются Полинами наилучшего среднеквадратичного приближения:

Итак, каждой функции из можно поставить в соответствие её ряд Фурье.

Какое отношение этот ряд Фурье имеет к функции?

Когда этот ряд в среднеквадратичном сходится к функции: Ответы на эти вопросы зависят от свойств ОНС.

Имеем:

неравенство Бесселя.

ОНС называется базисом в если её ряд Фурье в среднеквадратичной форме сходится к ней, т.е. можно записать равенство

ОНС называется замкнутой в если множество всех полиномов по система плотно в относительно среднеквадратичной сходимости, т.е.:

ОНС называется полной в если не существует в ненулевой функции, ортогональной всем функциям системы.

ОНС удовлетворяет равенству Парсеваля, если равна сумме квадратов коэффициентов Фурье, т.е.

Теорема. Все четыре условия на ОНС – равносильные.

Мы докажем более слабый вариант теоремы: является базисом тогда и только тогда, когда она замкнута. И в случае базиса выполняется неравенство Парсеваля.

Доказательство. Необходимость.

Достаточность.

Неравенство Парсеваля:

Доказано.

Для ортогональной системы и необязательно нормированной системы ряд Фурье, коэффициенты ряда Фурье и равенство Парсеваля выглядят следующим образом:

ряд Фурье, у которого коэффициенты Фурье имеют вид: равенство Парсеваля.