Лекция №30 Свойства несобственных интегралов, зависящих от параметра

Теорема 1. Если сходится равномерно на отрезке то

Доказательство. сходится равномерно на (из определения равномерной сходимости по Гейне) (из теоремы о равномерном пределе последовательности непрерывных функций)

Доказано.

Теорема 2. Если сходится равномерно на отрезке то и

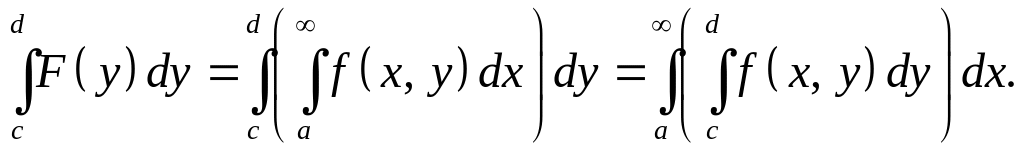
Доказательство. сходится равномерно на отрезке

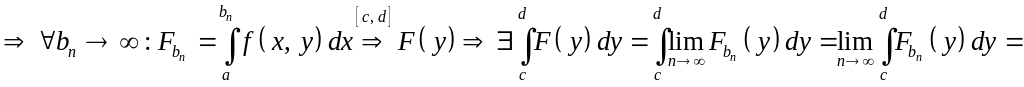
(по теореме об интегрируемости собственных интегралов) =

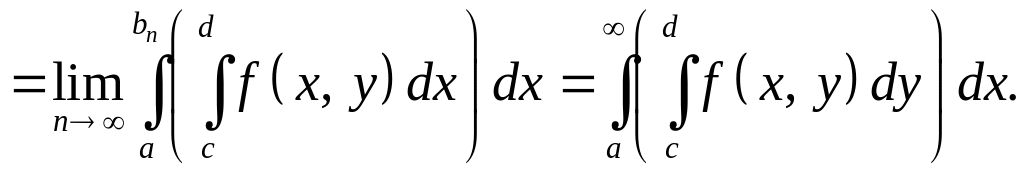
Доказано.

Теорема 3. Если

1. 

2. сходится;

3. сходится равномерно на то

Доказательство. сходится равномерно на

Доказано.

Свойства гамма-функции

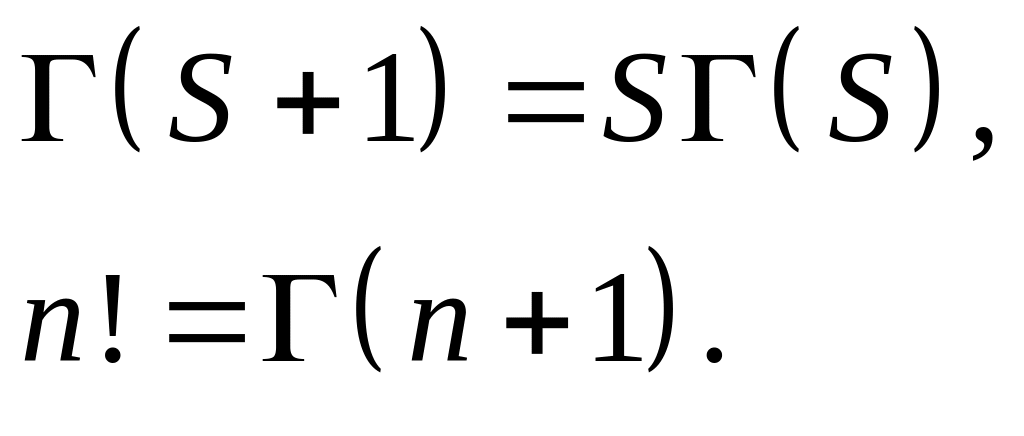
Лемма 1.

Доказательство. По формуле Эйлера

Доказано.

Лемма 2. Для

Доказательство. Сделаем замену тогда

Доказано.

Теорема 4. (*)

Доказательство.

1. Т.к.

2.

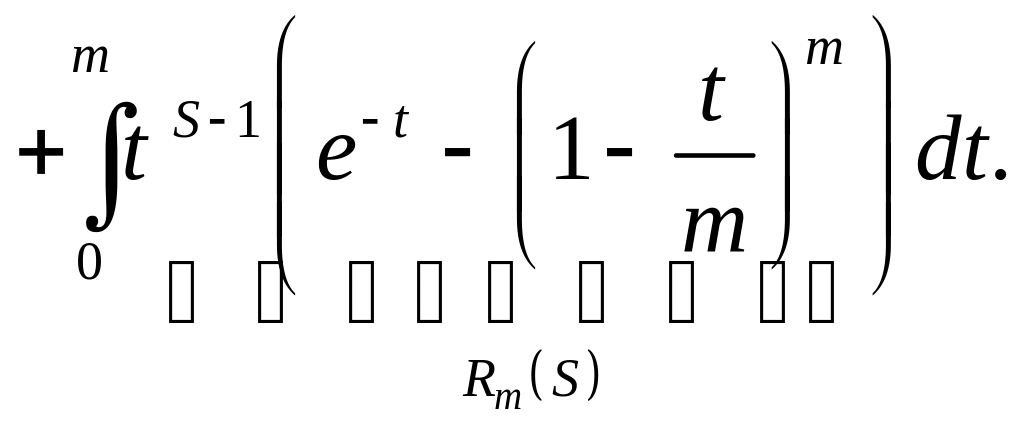
Из этого представления равенство (*) будет вытекать тогда и только тогда, когда

3. Введём вспомогательные неравенства.

(неравенство Бернулли).

Докажем это неравенство методом математической индукции.

При равенство очевидно.

верно.

4. Докажем, что

Докажем, что неравенство из (3) при

Оценим снизу:

Оценка сверху:

Итак,

и по теореме «о двух милиционерах»

Доказано.

Лемма 3. (подробнее это изучается в курсе теории функций комплексного переменного ТФКП).

Лемма 4. нецелого справедливо следующая формула дополнения В частности, при

Доказательство. Имеем по формуле Эйлера

Доказано.

Задача. Вычислить

Лекция№31 Преобразование Фурье

Пусть дана функция несобсттвенный интеграл от функции по всей прямой абсолютно сходящийся в смысле Коши. Главное значение

Рассмотрим несобственный интеграл, зависящий от параметра.

называемый преобразованием Фурье функции (Это и есть аналог коэффициентов Фурье в периодическом случае.)

Лемма 1. Если и интеграл абсолютно сходящийся по Коши, то

Доказательство. По соответствующей теореме достаточно проверить равномерную сходимость преобразования Фурье на множестве действительных чисел, т.к.

Воспользуемся признаком равномерной сходимости Вейерштрасса:

сходится. Значит, преобразование Фурье сходится равномерно.

Доказано.

Лемма 2. Если то

Доказательство. Также воспользуемся соответствующей теоремой; проверим следующие условия:

1. непрерывность:

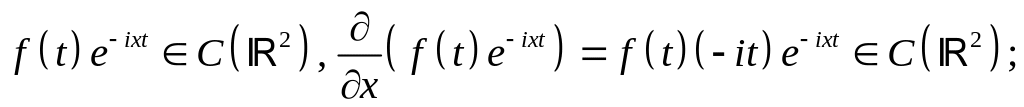
2. равномерная сходимость (признак Вейерштрасса):

Следствие. Если сходится, то

Иногда испоьзуют и действительную форму преобразования Фурье, тогда появляется косинус-преобразование Фурье:

и синус-преобразование Фурье:

Тогда обычное преобразование Фурье есть обычная их комбинация:

Лемма 3. если

Доказательство.

Доказано.

Следствие. если

Например, в уравнение теплопроводности удобно перейти к по переменной t: потом функцию необходимо восстановить.

Сама функция по её преобразованию Фурье восстанавливается с помощью обратного преобразования Фурье: аналогичное тригонометрическому ряду Фурье.

Частичные интегралы – аналог сумм: И вопрос состоит в следующем: сходится ли при

Различабт сходимости среднеквадратичную: и поточечную: в точке и равномерную:

Пример. Найти преобразование Фурье функции

Замечание. Часто преобразование Фурье определяют формулой

тогда обратное преобразование Фурье имеет вид:

Справедливы следующие утверждения.

Теорема 1. Если абсолютно интегрируема на то

Теорема 2. Если абсолютно интегрируема на и кусочно-непрерыно-дифференцируема на то

Теорема 3. Если абсолютно интегрируема на и кусочно-непрерывно-дифференцируема на то имеет место равномерная сходимость

Вопросы по курсу математического анализа за III осенний семестр