Лекция №10 Бесконечные произведения (продолжение)

Для дальнейшего удобно обозначить и рассматривать (3), (4), (5).

Теорема. Произведение (3) – сходится абсолютно (4) сходится абсолютно.

Доказательство. (3) сходится абсолютно сходится и в частности . Сравним ряды и при условии : для . Из этих неравенств вытекает, что эти ряды сходятся абсолютно.

Доказано.

Следствие: если в произведении (3) все b_n, начиная с некоторого номера, имеют один и тот же знак, то сходимость произведения (3) эквивалентна сходимости ряда (4).

Пример. расходится.

Анализ этой теоремы показывает, что удобно использовать разложение .

Задача. Обозначим: «+» - сходится, «-» - расходится, и заполним следующую таблицу:

	(4)	(5)	(3)
1.	+	+	+
2.	+	-	-
3.	-	+	-
4.	-	-	?

Доказательство 1. , - сходятся

. Доказано.

Пример. сходится, т.к. сходится, но расходится.

Доказательство 2. Опять и из признака сравнения ряд расходится. Общий член есть сумма двух последовательностей – сходящейся и расходящейся, значит, ряд расходится, иначе ряд был бы сходящимся как разность двух сходящихся рядов. Доказано.

Доказательство 3. Опять

И как в предыдущем случае ряд сходится.

Доказано.

Доказательство 4. Два примера:

1. “-”, “-” “-” ;

2. “-”, “-” “+”.

Ряд Частичная сумма порядка совпадает с частичной суммой гармонического ряда, т.е. ряд расходится.

расходится. Оба ряда расходятся.

Вычислим частичное произведение

т.к. произведение расходится по следствию: обобщённый гармонический ряд с показателем p = - сходится.

сходится к тому же числу, а значит и всё произведение сходится.

Доказано.

Лекция №11 Функции, представляющиеся в виде бесконечных произведений

Многие элементарные функции раскладываются в бесконечные произведения, например, . С помощью бесконечного произведения можно определять и новые функции, называемые спиральными, например  - функция (гамма-функция): константа Эйлера, . Проверим, что для всех указанных S бесконечное произведение действительно сходится и определяет некоторую функцию. Проверим сходимость следующего ряда:

.

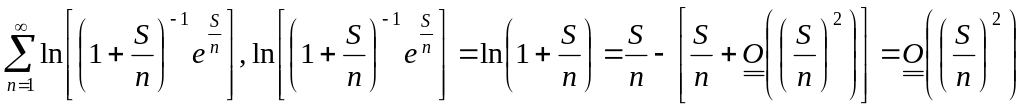сходится .

Свойства  - функции.

1. Формула Эйлера: .

2. Основное функциональное тождество для  - функции:

В частности, .

Рассмотрим поведение n! для больших n:

формула Стирлинга

Доказательство 1.

Сравнивая (*) и (**), получим формулу Эйлера.

Доказано.

Доказательство 2. Рассмотрим отношение . По формуле Эйлера получаем:

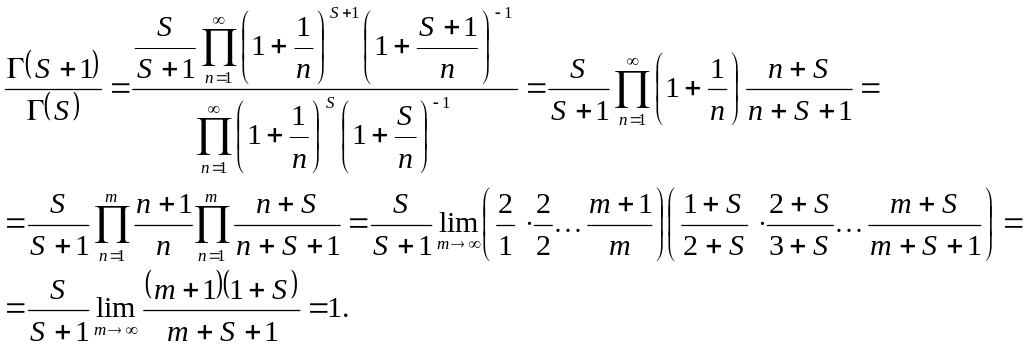
Доказано.

Функциональные последовательности и ряды

1. Определение функциональной последовательности и функционального ряда

Сумма геометрической прогрессии сходится.

Пусть последовательность функций, определённых на одном и том же множестве

Функциональный ряд – это ряд вида .

Определим область сходимости (поточечной сходимости) для функциональной последовательности и функционального ряда: предельная функция. Аналогично для функционального ряда область сходимости (поточечной сходимости) функционального ряда, а сумма функционального ряда.