4.2. Поворот осей координат

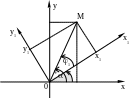
Рис.4.2

Из рис.4.2 видно, что , , , .

Учитывая, что , из этих формул получим:

Окончательно, получим:

(4.2.1)

или (4.2.2)

Замечание 1. Формулы (4.2.2) можно получить из соотношений (4.2.1), рассматривая их как уравнения, определяющие и через и , и разрешая их относительно и .

Замечание 2. Формулы (4.2.2) называют формулами обратного перехода, которые выражают координаты и через и .

Рассмотрим матрицу и векторы и .

Матрица невырожденная, т.к. определитель этой матрицы отличен от нуля

.

Тогда формулы (4.2.1) в матричном виде имеют вид , т.е.

, (4.2.3)

а формулы (4.2.2) имеют вид , т.е.

(4.2.4)

можно проверить, что .

- обратная матрица матрицы .

- транспонированная матрица матрицы .

.

5. Кривые второго порядка

Любое уравнение второго порядка вида Ах2+2Вocy+Сy2+Ех+Dх+F=0 определяет на плоскости одну из след. кривых: окружность, эллипс, гиперболу, параболу или, в особых случаях, пару прямых или точки.

Мы не будем доказывать это утверждение, а приведем лишь канонические уравнения перечисленных линий второго порядка и их геометрические изображения.

5.1. Окружность

Окружность - геометрическое место точек, равноудаленных от центра (рис.5.1)

Рис. 5.1.

5.2. Эллипс

Эллипс - геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух данных точек F₁ и F₂ той же плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а и большая, чем расстояние между фокусами 2с. Выведем уравнение эллипса, исходя из данного определения. Выберем систему координат как показано на рис 5.2

(Расстояния любой точки M(x,y) эллипса до фокусов называются ее фокальными радиусами. Пусть M(x,y) - произвольная точка эллипса, числа r₁ и r₂ –фокальные радиусы т. M:

r₁ =F₁M; r₂=F₂M; r₁ +r₁=2а (см. рис.5.2), тогда r₁= а - х; r₁ = а + х (5.2.1), где , а - большая полуось эллипса, с - половина расстояния между фокусами. Формулы (5.2.1) линейно выражают фокальные радиусы любой точки эллипса через ее абсциссу.)

r₁ = F₁M = ; r₂ = F₂M =

F₁M + F₂M = + = 2а

Это уравнение эллипса приведем к более простому виду: возводя дважды это уравнение в квадрат и преобразуя его, получим:

x² + 2xc + c² + y² = 4a² - 4a + x² - 2xc² + y²;

xc - a² =-a ; x²c² - 2xca² + a⁴ = a²(x² - 2xc + c²) + a²y;

x²(c² - a²) - a²y² = a²c² - a⁴; x²(a² - c²) + a²y² = a²(a² - c²); x²b² + a²y² = a²b²,

где положили а² - с² = b². Деля обе части последнего равенства на a²b², получим каноническое уравнение эллипса; 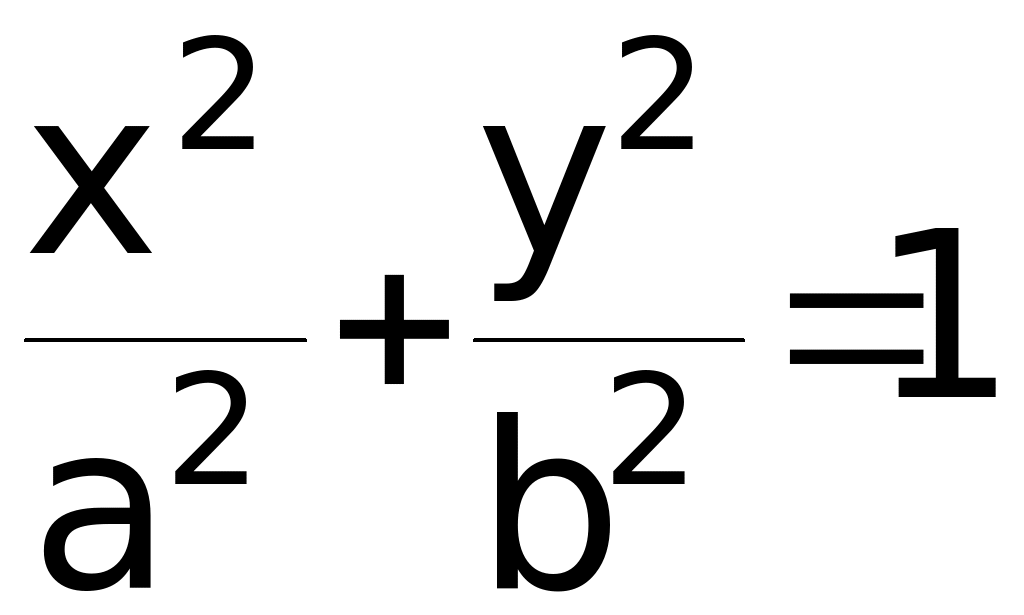(5.2.2)

Как видно из этой формулы эллипс симметричен относительно осей OX и OY, т.к. вместе с точкой (x,y) ему принадлежат и точки (-x,-y), (-x, y), (x, -y). Точки пересечения с осями называются вершинами эллипса и равны x = 0; y = b; y = 0; x = a (5.2.3)

Определение: Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.

Обозначив эксцентриситет через , получим (5.2.4)

Эксцентриситет характеризует форму эллипса. Эксцентриситет эллипса содержится в промежутке (0, 1).