6.8. Уравнение прямой в пространстве
В пространстве, так же как и на плоскости, одну и ту же прямую можно определить разными по форме уравнениями.
Рассмотрим несколько случаев.
6.8.1. Общие уравнения прямой
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей:
(6.8.11)
6.8.2. Параметрические и канонические уравнения прямой
Пусть дана точка M0(x0, y0,
z0) прямая l и задан направляющий
вектор
(m,
n, p) (вектор
параллелен прямой l).
Рис. 6.4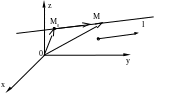
Составим уравнение прямой l.
Возьмём на прямой произвольную точку
М(x,y,z)
и проведём радиус-векторы
=
(x0,y0,z0)
и
=
(x,y,z).
Вектор
=
-
=
-
лежащий на прямой l,
по условию коллинеарен вектору S,
поэтому
(6.8.2.1)
где t - параметр. Равенство (6.8.2.1) перепишем иначе:
-
=
или
=
+
(6.8.2.2)
Это векторное уравнение прямой.
Уравнение (6.8.2.2.) в проекциях:
x = x0 + mt, y = y0 + nt, z = z0 + pt (6.8.2.3.)
Эти уравнения называются параметрическими уравнениями прямой.
Если исключить параметр t из уравнения (6.8.2.3.), получим:
(x - x0)/m = (y - y0)/n = (z-z0)/p (6.8.2.4)
Уравнения (6.8.2.4.) называется каноническими уравнениями прямой.
Уравнения (6.8.2.4.) умножим на
и запишем их в таком виде:
(x - x0)/m/s = (y - y0)/n/s = (z - z0)/p/s или (x - x0)/cos = (y - y0)/cos = (z - z0)/cos,
где ,, - углы, образованные прямой с осями координат Ox, Oy, Oz. Величины cos, cos, cos называются направляющими косинусами прямой и вычисляются с помощью формул:
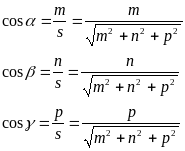(6.8.2.5.)
Замечание. Прямая (6.8.2.4.) определяемая системой (x-x0)/0 = (y-y0)/0 = (z-z0)/p параллельна оси Oz.
6.8.3. Уравнения прямой, проходящей через две заданные точки
Пусть прямая проходит через две данные точки М1(x1,y1,z1) и М2(x2,y2,z2). В этом случае можно положить, что направляющий вектор прямой = (x2 - x1, y2 - y1, z2 - z1)
Подставив в уравнения (6.8.2.4.) m = x2-x1, n = y2 - y1, p = z2 - z1, x0 = x1, y0 = y1, z0 = z1, получим (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) = (z - z1)/(z2 - z1) (6.8.3.1)
Это уравнение прямой, проходящей через две данные точки.
Замечание. 1. Три точки М1 ,М2 ,М3 лежат на одной прямой, если выполняется условие (x3 - x1)/(x2 - x1) = (y3 - y1)/(y2 - y1) = (z3 - z1)/(z2 - z1)
2. От общих уравнений прямой (6.8.1.1.) можно перейти к каноническим уравнениям (6.8.2.4) и наоборот.
6.9. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
Пусть даны прямые l1 и l2:
(x-x1)/m1=(y-y1)/n1=(z-z1)/p1 (6.9.1)
(x-x2)/m2=(y-y2)/n2=(z-z2)/p2 (6.9.2)
Определение. Углом между двумя
прямыми l1
и
l2
называется угол между их
направляющими векторами
(m1,n1,p1)
и
(m2,n2,p2)
(рис.6.5.).
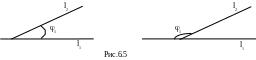
(6.9.3)
Если прямые (6.9.1) и (6.9.2) параллельны, то и коллинеарны. Отсюда получаем условие параллельности прямых:
m1/m2 = n1/n2 = p1/p2 (6.9.4)
Если прямые (6.9.1.)и (6.9.2.) взаимно перпендикулярны, то и также перпендикулярны и их скалярное произведение равно нулю, т.е. ( ) = 0
m1m2 + n1n2 + p1p2 = 0 (6.9.5.)
Это условие перпендикулярности двух прямых
6.10. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Пусть даны прямые: (x-x0)/m = (y-y0)/n = (z-z0)/p (6.10.1)
и плоскость Ax + By + Cz + D (6.10.2)
Углом между прямой l и плоскостью называется угол (0<=<=/2), образованный прямой с её проекцией на плоскость (рис.6.6.)
Из рис. 6.6. видно, что угол между (A,B,C) плоскости и (m,n,p) - направляющим вектором прямой равен /2 - , поэтому
(6.10.3)
Условие перпендикулярности прямой (6.10.1) и плоскости (6.10.2) совпадает с условием коллинеарности векторов и , поэтому это условие запишется в виде:
или
A/m = B/n = C/p (6.10.4)
Условие же параллельности прямой
(6.10.1) и плоскости (6.10.2) совпадает с
условием перпендикулярности векторов
и
;
следовательно, получим:
или
Am
+
Bn
+
Cp
=
0
(6.10.5)