3. Прямая линия
3.1. Параметрические и канонические уравнения прямой
Положение прямой l однозначно
определяется точкой M0
на прямой и вектором
,
коллинеарным ей. Вектор
называется направляющим вектором
прямой.
Пусть
-
текущая точка на прямой l, т.е.
точка, пробегающая всю прямую, и пусть
Oxyz - прямоугольная декартова система.
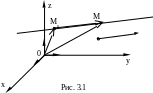
Векторы
и
коллинеарны (рис. 3.1.).
,
где
- число
,
или
(3.1.1)
Уравнение (3.1.1.) носит название векторного
параметрического уравнения прямой.
Очевидно, что уравнение (3.1.1.) справедливо
для векторного пространства любой
размерности. Скалярные уравнения прямой
в пространстве получим с помощью
координат векторов и точек. Обозначим
координаты точек
и
,
если изучается прямая на плоскости, и
через
и
,
если прямая в пространстве, соответственно
координаты направляющего вектора
обозначим
и
.
Тогда получим параметрические уравнения
прямой:
для плоскости
(3.1.2)
для пространства
(3.1.3)
Решая уравнение (3.1.2) относительно
, получим канонические уравнения:
для плоскости
(3.1.4)
для пространства
(3.1.5)
Аналогично могут быть получены уравнения прямой в пространстве любой размерности.
Перепишем уравнения (3.1.2) в виде (получается исключением из (3.1.2))
(3.1.6)
где
называется угловым коэффициентом прямой
на плоскости,
,
где
,
называемый углом наклона прямой l
к оси Ox, равен углу, который прямая
образует с положительным направлением
оси Ox. Этот угол считается положительным,
если он отсчитывается от оси Ox
против часовой стрелки, и отрицательным
- по часовой стрелке (3.1.2).
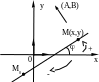
Рис. 3.2.
Преобразуя уравнение (3.1.6), получим уравнение прямой с угловым коэффициентом
,
где
(3.1.7)
Уравнение прямой, проходящей через две
заданные точки
и
,
получим из уравнения (3.1.2) заменой
на
и
на
(за направляющий вектор можно взять
вектор
)
(3.1.8)
3.2. Общее уравнение прямой на плоскости
Положение прямой на плоскости однозначно определяется заданием точки на прямой и вектором, перпендикулярным (нормальным) к ней (рис. 3.2).
(3.2.1)
где
,
,
Уравнение Ах+Ву+С=0 называется общим
уравнением прямой. Желательно запомнить,
что вектор
,
проекции которого на оси координат
равны соответствующим коэффициентам
при x и у, является
перпендикулярным (нормальным) к прямой.
3.3. Основные задачи на прямую на плоскости
1. Углом между двумя прямыми
и
называется
угол, на который нужно повернуть первую
прямую
до совмещения со второй. Этот угол
положительный, если поворот происходит
против часовой стрелки, и отрицательный
- если по часовой (рис.3.3).
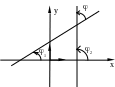
Рис. 3.3
Из рис. 3.3 видно, что
,
если
и
.
Итак, получим формулу:
(3.3.1)
Условие параллельности прямых
и
: 
,
т.е. угловые коэффициенты равны.
Условие перпендикулярности прямых
и
:
т.е.
произведение угловых коэффициентов
равно -1.
2. Один из углов между прямыми равен углу между нормалями к ним, а угол между векторами (нормалями) находится из формулы:
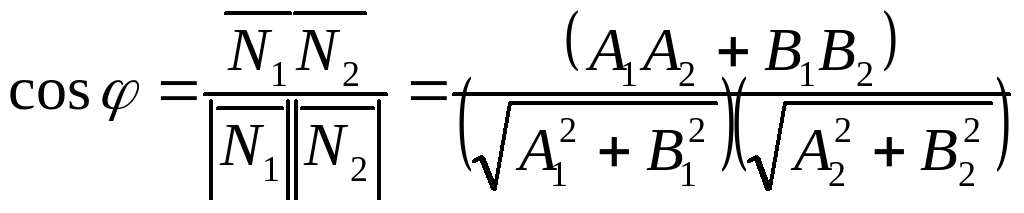, (3.3.2)
где
и
нормали к прямым
и
.
Условие параллельности прямых:
,
т.е. у параллельных прямых коэффициенты
при неизвестных пропорциональны.
Условие перпендикулярности прямых:
3. Расстояние от точки
до прямой на плоскости равно длине
перпендикуляра, опущенного из точки
на
прямую, который в свою очередь равен
абсолютной величине проекции вектора
на
нормаль к прямой, где
-
любая точка, лежащая на прямой
.
Имеем (рис.3.4)
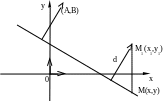
Рис.3.4
(3.3.3)
т.е. расстояние равно абсолютной величине
дроби, числителем которой является
число, получаемое подстановкой координат
точки
в левую часть общего уравнения прямой,
а знаменателем - длина нормали к прямой.
3.4. Уравнение пучка прямых на плоскости
Пучком прямых, проходящих через заданную точку (центр пучка), называется множество всех прямых, проходящих через эту точку.
Если точка
задана своими координатами, то уравнение
пучка может быть записано в виде либо
,
либо
.
Если же точка задана точкой пересечения
прямых
и
,
то уравнение пучка имеет вид
(3.4.1)
где
-
действительное число.
3.5. Решение типовых задач к разделу 3
3.5.1. Найти уравнение окружности радиуса R с центром в точке C(a,b)
Решение. По определению окружности расстояние любой точки M(x,y), лежащей на окружности, от ее центра C(a,b) равно длине радиуса R, т.е. CM=R.
Найдем длину отрезка CM и выразим равенство CM=R с помощью текущих координат точки M:
3.5.2. Найти
точки пересечения линий
и
Решение. Система уравнений
имеет два решения:
и
,
следовательно, данные линии имеют две
общие точки
и
.
3.5.3. Составить
уравнение прямой линии, образующей с
осью Ох угол 60° и пересекающей ось Оу в
точке (0,-2). Выяснить, проходит ли эта
прямая через точки А(
,1)
и В (2,5)
Решение. Из условия задачи следует,
что начальная ордината b=-2, угловой
коэффициент
,
следовательно, по формуле (3.1.7) имеем
.
Подставляя в искомое уравнение прямой координаты точки А вместо текущих координат, получим 1=3-2, т.е. 1=1.
Прямая проходит через точку А( ,1).
Аналогично, подставляя в уравнение
координаты точки B, получим:
.
Прямая не проходит через точку В.
3.5.4.
Уравнение
привести к уравнению с угловым
коэффициентом
Решение. Данное уравнение решим
относительно
,
получим уравнение
.
Отсюда видно, что
,
.
3.5.5. Написать уравнение прямой, проходящей через данные точки А(2,-5) и В(1,3)
Решение. Используя формулу (3.8) запишем уравнение данной прямой
3.5.6. Написать
уравнение прямой проходящей через точку
Параллельно вектору
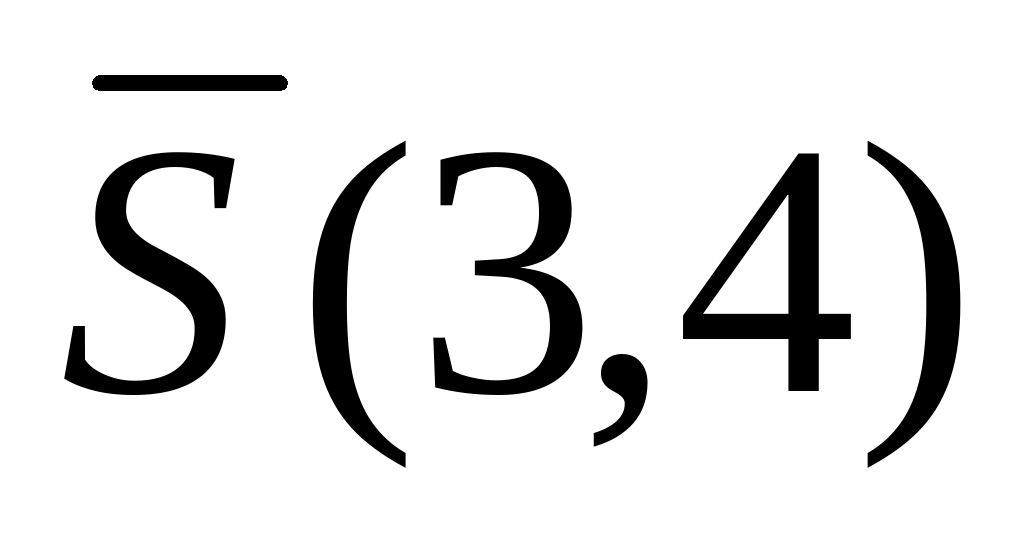.Перпендикулярно вектору
.
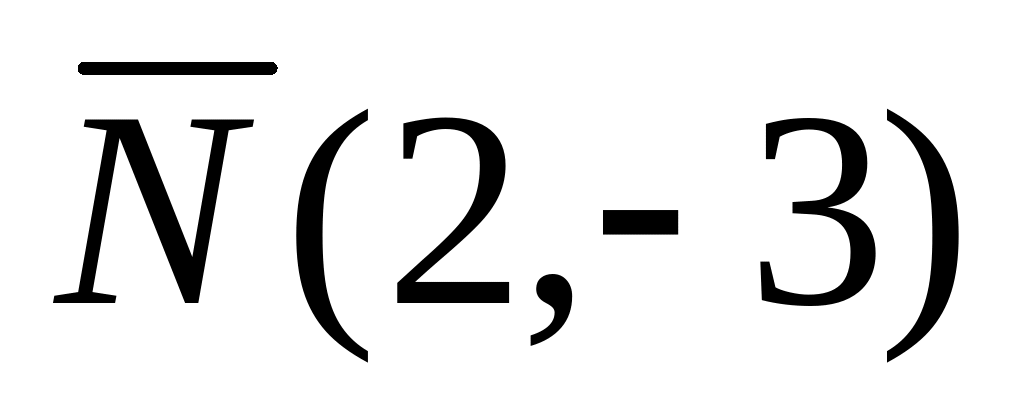Решение.
Используя каноническое уравнение прямой (3.5), имеем
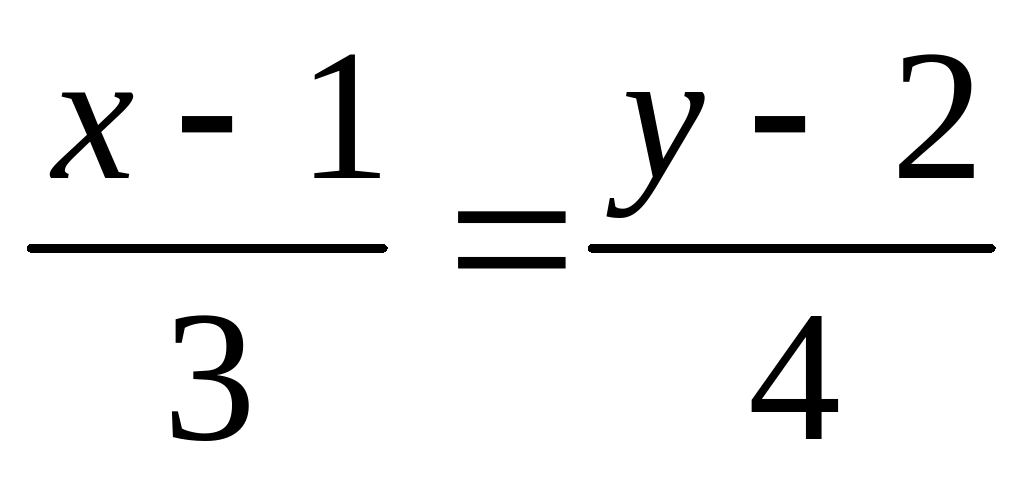или
.Используем уравнение (4.1):
.
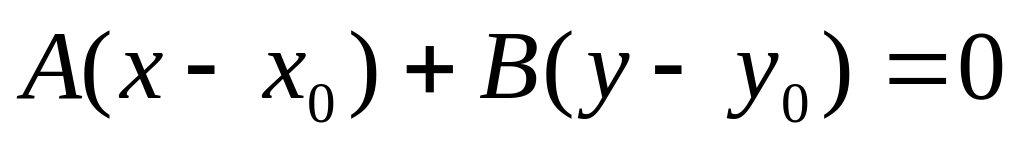Имеем
или
.
3.5.7. Найти
координаты M(x,y,z),
делящей отрезок M1M2
в отношении
,
если M1(1,2,3), M2(3,9,-2)
Решение. Используем формулы деления отрезка в заданном отношении .
,
,
,
,
,
(3.5.7)
3.5.8. Найти
угол между прямыми
и
Решение. По формуле (3.3.1) получим
,
где
,
,
.
Здесь угол отсчитывается от прямой .
3.5.9. Выбрать
значение коэффициента
прямой
таким, чтобы эта прямая была:
Параллельна прямой
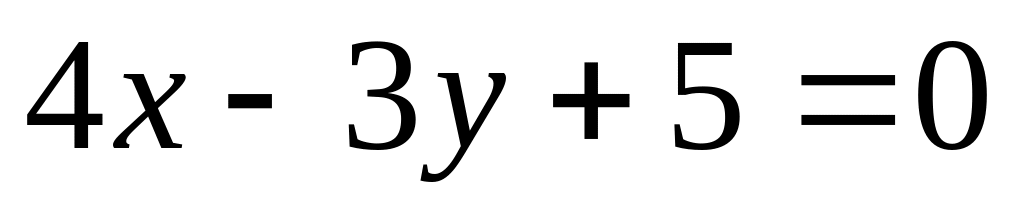.Перпендикулярна прямой
.
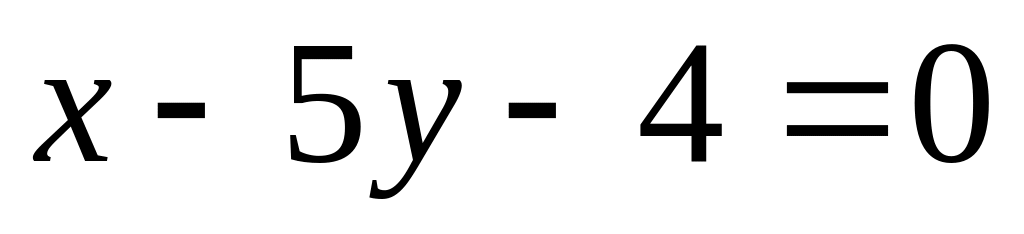Решение.
Используя условие параллельности прямых, получим
,
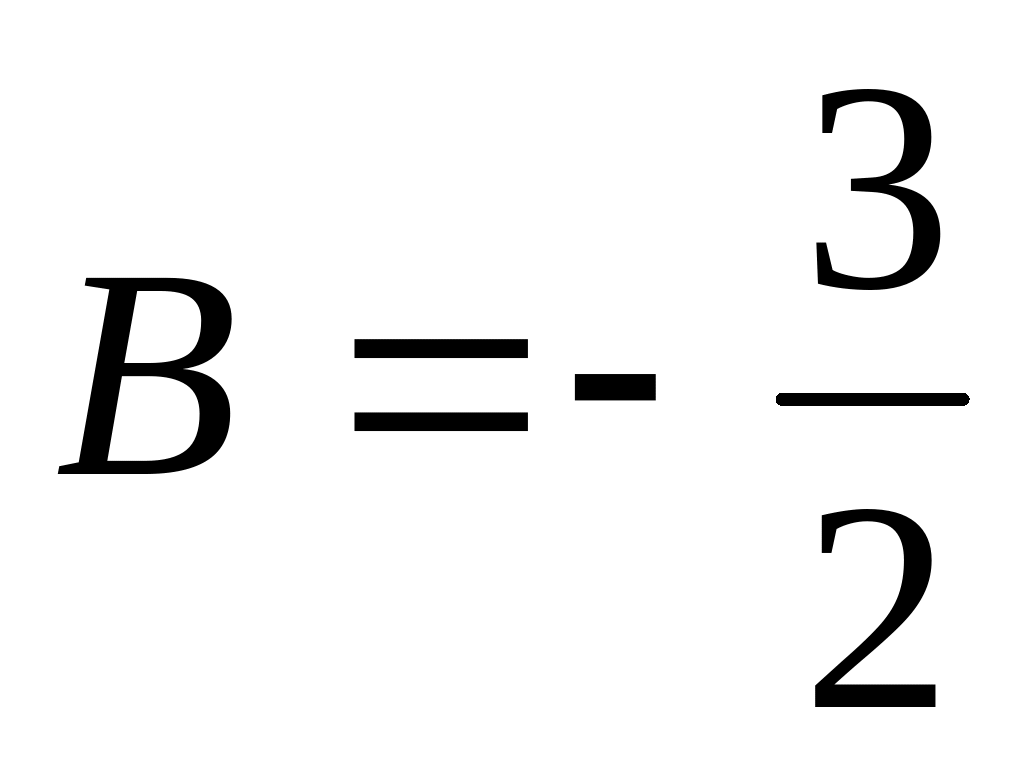.Используя условие перпендикулярности прямых, получим
,
.
3.5.10. Найти
уравнение прямой, проходящей через
точку пересечения прямых
и
,
а также:
а). точку
,
б). перпендикулярно прямой
Решение.
Используем уравнение пучка прямых, проходящих через точку пересечения данных прямых
.
Имеем
.
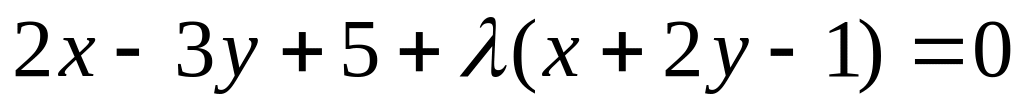Число
найдем
из условия, что прямая должна проходить
через точку
:
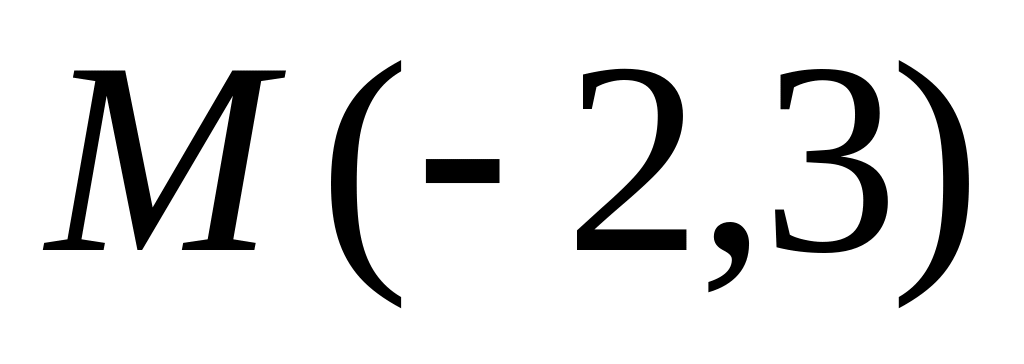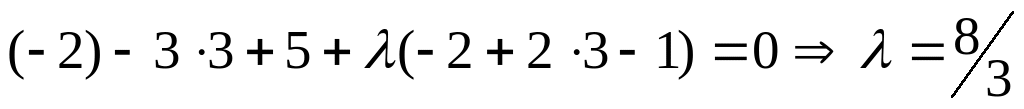Подставляя найденное значение
в уравнение пучка, получим
.
Используя условия перпендикулярности прямых, можем записать
.
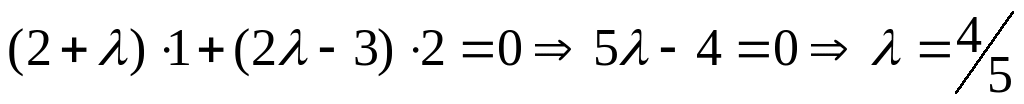Подставляя в уравнение пучка, получим
.
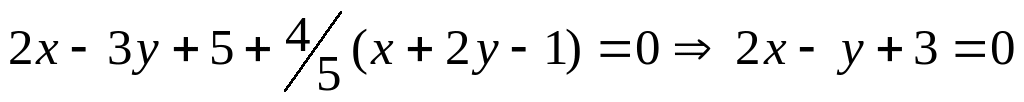3.6. Задачи для самостоятельной работы
3.6.1. Найти угловой коэффициент каждой из прямых, которые заданы уравнениями:
1. 
.
2. 
.
3. 
.
4. 
.
3.6.2. Написать уравнение прямой, пересекающей
ось Ох в точке с ординатой
и образующей с осью Ох угол
.
3.6.3. Определить острый угол между прямыми
и
.
3.6.4. Через начало координат провести
параллельную и перпендикулярные прямые
к данной прямой
.
3.6.5. Через точку
провести прямую, перпендикулярную к
прямой
.
3.6.6. Через точку пересечения прямых
и
провести прямую так, чтобы она прошла,
кроме того, и через точку
.
3.6.7. Через точку пересечения прямых
и
провести прямую под углом
к первой из них.
Указание. Использовать формулы (3.4.1) и (3.3.1).
3.6.8. Найти уравнение прямой, проходящей
через точку
и образующей в I четверти с осями координат
треугольник, площадь которого равна
16.
Указание. Уравнение прямой находится по формуле:
(3.6.8)
Это уравнение прямой называется уравнением в отрезках.