1.2. Проекция вектора

Проекцией вектора на заданную ось l называется величина вектора на оси l (рис. 1.5а). Проекцией вектора на вектор называется проекция вектора на ось, проходящую через вектор и имеющую с ним одинаковое направление (рис. 1.5б).

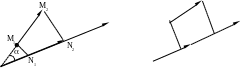
Рис. 1.5а Рис. 1.5б

Пр , где - угол между вектором и осью l.

Свойство проекций:

1) Проекция суммы векторов на ось равна сумме проекций этих векторов, т.е. Пр_l Пр_l + Пр_l ;

2) проекция произведения вектора на число равна произведению числа на проекцию вектора , т.е. Пр_l Пр_l .

1.3. Декартовы прямоугольные координаты

Положение точки в пространстве будем определять относительно пространственной декартовой прямоугольной системы координат, состоящей из трех взаимно перпендикулярных осей координат, пересекающихся в одной и той же точке О, называемой началом координат.

Ось Ox называют осью абсцисс, ось Oy - осью ординат и ось Oz - осью аппликат.

Координатные оси Ox, Oy, Oz, взятые попарно, определяют три взаимно перпендикулярные плоскости xOy, yOz, xOz, называемые координатными плоскостями.

Декартова система координат позволяет связать с каждой точкой P пространства, в котором выбраны три не лежащие в одной плоскости направленные прямые Ox, Oy, Oz (оси координат), пересекающиеся в начале O, три вполне определенных действительных числа (декартовы координаты) x, y, z; при этом пишут P(x, y, z).

Оси Ox, Oy, Oz могут образовывать правую или левую систему. Для правой системы поворот от оси Ox к оси Oy на угол, меньший , совершается в направлении против часовой стрелки, если смотреть на плоскость xOy из какой-либо точки положительной полуоси Oz (положительная сторона плоскости xOy). Смотрите рис.1.6.

Правая система Левая система

Рис. 1.6

Замечание. Наряду с декартовой системой координат рассматривается полярная система координат на плоскости, которая задается точкой О (полюсом) и полярной осью - лучом, выходящим из полюса. Связь прямоугольных и полярных координат задается формулами:

, где (1.3.1)

1.4. Координатное представление векторов

Пусть мы имеем прямоугольную систему координат в пространстве. Обозначим единичные векторы (орты ) осей Ox, Oy, Oz соответственно через причем .

Разложим произвольный вектор трехмерного пространства по ортам. Для этого построим вектор , равный вектору . Из точки М опустим перпендикуляр на плоскость хOу. Из основания этого перпендикуляра (точка А) опустим перпендикуляры на оси координат Ох и Оу и соединим точку А с началом О. На векторах и построим прямоугольник ОАММ3, диагональю которого будет вектор . Из рис. 1.7 видно, что или .

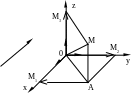
Рис. 1.7

Векторы , , называются составляющими или компонентами вектора , а их величины | |=Х, | |=Y, | |=Z координатами этого вектора.

Определение 1. Проекции вектора на соответствующие координатные оси называется его составляющими или компонентами.

Определение 2. Величины проекций вектора на соответствующие координатные оси называются его координатами.

Компоненты вектора выразим через его координаты и единичные векторы : =Хi, =Yj, =Zk .

Подставляя эти значения в равенство и обозначив через получим:

(1.4.1)

Равенство (1.4.1) можно записать в виде:

(1.4.2)

Замечание 1. Равные векторы имеют одинаковые координаты.

Замечание 2. Разложение вектора в виде (1.4.1) возможно только единственным способом.

Из единственности разложения (1.4.1) вектора по ортам, следует, что если координаты любых двух векторов и равны, т.е. , то эти векторы тоже равны .

Вектор , идущий от начала точки О к точке называется радиус - вектором этой точки, и его координаты совпадают с соответствующими координатами точки (рис. 1.8), Х=х, Y=y, Z=z.

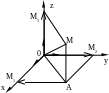
Рис. 1.8

Поэтому , или . Пусть - вектор, координаты начала и конца которого известны и . Тогда координаты вектора выражаются по формулам :

(1.4.3)

Из рис. 1.9 видно, что

(1.4.4)

x

Рис. 1.9

Используя свойства проекций (п.1.2.), имеем: , и аналогичным образом находим .

Разложение вектора по ортам будет иметь следующий вид:

(1.4.5)

Тройка векторов называется координатным базисом, а разложение (1.4.1) вектора называется разложением вектора по базису .

Замечание. Разложение вектора на плоскости по базису имеет вид .