
- •Содержание
- •5.8. Задачи для самостоятельной работы 29
- •5.9. Вопросы для самопроверки 31
- •6.11.3. Вопросы для самопроверки 40
- •7.6. Задачи для самостоятельной работы 46
- •Введение
- •1. Элементы векторной алгебры
- •1.1. Векторы в евклидовом пространстве
- •1.2. Проекция вектора
- •1.3. Декартовы прямоугольные координаты
- •1.4. Координатное представление векторов
- •1.5. Операции над векторами, заданными в координатной форме
- •1.6. Скалярное произведение векторов
- •1.6.1. Свойства скалярного произведения:
- •1.6.2. Скалярное произведение векторов, заданных координатами
- •1.6.3. Угол между векторами
- •1.6.4. Условия коллинеарности и перпендикулярности векторов
- •1.7. Векторное произведение двух векторов
- •1.7.1. Свойства векторного произведения
- •1.7.2. Координатная форма записи векторного произведения
- •1.8. Смешанное (векторно - скалярное) произведение векторов
- •1.8.1. Свойства смешанного произведения
- •1.8.2. Координатная форма записи смешанного произведения
- •1.9. Двойное векторное произведение трех векторов
- •1.10. Вопросы для самопроверки
- •Свойства скалярного произведения.
- •Координатная форма записи векторного произведения.
- •2. Понятие об уравнениях линий и поверхностей
- •3. Прямая линия
- •3.1. Параметрические и канонические уравнения прямой
- •3.2. Общее уравнение прямой на плоскости
- •3.7. Вопросы для самопроверки к разделу 3
- •4.2. Поворот осей координат
- •5. Кривые второго порядка
- •5.1. Окружность
- •5.2. Эллипс
- •5.3. Гипербола
- •5.4. Директрисы эллипса и гиперболы
- •5.5. Парабола
- •5.6. Уравнения эллипса, гиперболы и параболы в полярных координатах
- •5.7. Решение типовых примеров
- •5.8. Задачи для самостоятельной работы
- •Ответы к 5.8
- •5.9. Вопросы для самопроверки
- •Ответы к 5.9
- •Окружность.
- •6. Плоскость и прямая в пространстве
- •6.1. Общее уравнение плоскости
- •6.2. Уравнение в отрезках
- •6.3. Векторное и нормальное уравнение плоскости
- •6.4. Расстояние от точки до плоскости
- •6.5. Взаимное расположение двух плоскостей
- •6.6. Пучок плоскостей
- •6.7. Уравнение плоскости, проходящей через три заданные точки
- •6.8. Уравнение прямой в пространстве
- •6.8.1. Общие уравнения прямой
- •6.8.2. Параметрические и канонические уравнения прямой
- •6.8.3. Уравнения прямой, проходящей через две заданные точки
- •6.9. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
- •6.10. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •6.11. О решение задач аналитической геометрии на плоскость и прямую
- •6.11.1. Примеры решения типовых задач
- •6.11.2. Задачи для самостоятельного решения
- •6.11.3. Вопросы для самопроверки
- •Ответы к 6.11.2
- •Ответы к 6.11.3
- •7. Краткое описание различных видов поверхностей второго порядка
- •7.1. Распадающиеся поверхности
- •7.2. Цилиндрические поверхности
- •7.3. Конусы второго порядка
- •7.4. Эллипсоиды и гиперболоиды
- •7.5. Параболоиды
- •7.6. Задачи для самостоятельной работы
- •Ответы к 7.6
- •Контрольное задание
- •Контрольные вопросы
- •7. Условия коллинеарности и перпендикулярности векторов.
- •Ответы к контрольному заданию
- •Литература
7.1. Распадающиеся поверхности
Пусть F(x,y,z) есть произведение двух многочленов первой степени:
F(x,y,z)=(A1x+B1y+C1z+D1)(A2x+B2y+C2z+D2) (7.1.1.),
то поверхность распадается на пару плоскостей: Ax1+B1y+C1z+D1=0 и Ax2+B2y+C2z+D2=0.
7.2. Цилиндрические поверхности
Цилиндрическая поверхность второго порядка задается в некоторой надлежаще выбранной для данной поверхности канонической системе координат уравнением:
F(x,y)=0 (7.2.1.)
Кривая, определяемая уравнением (7.2.1.) в плоскости Oxy, является направляющей кривой цилиндрической поверхности. Эта кривая может быть эллипсом, действительным или мнимым, гиперболой или параболой, в зависимости от чего мы и различаем эллиптические (рис. 7.1.), мнимые эллиптические, гиперболические (рис. 7.2.) и параболические (рис. 7.3.) цилиндры, канонические уравнения которых совпадают с каноническими уравнениями направляющих кривых.
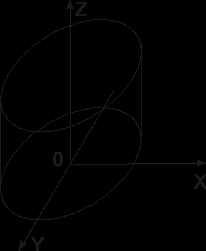
рис.7.1. Эллиптический цилиндр. Каноническое
уравнение
![]()

рис.7.2. Гиперболический цилиндр.
Каноническое уравнение
![]() .
.
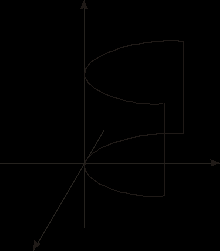
рис.7.3. Параболический цилиндр. Каноническое уравнение x2=2pZ.
Замечание. Если направляющая (7.2.1) есть пара прямых, то цилиндрическая поверхность выражается в пару плоскостей (пересекающихся, параллельных или совпадающих, действительных или мнимых - в зависимости от соответствующего свойства лежащей в основании пары прямых).
7.3. Конусы второго порядка
Под действительным конусом второго порядка понимается поверхность второго порядка, которая в прямоугольной системе координат задается уравнением:
![]() (7.3.1.)
(7.3.1.)
Это уравнение и система координат, в которой данный конус задается, называются каноническими для этого конуса (рис.7.4.).
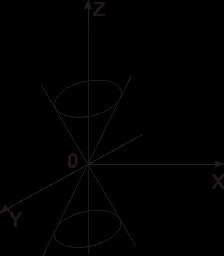
рис.7.4.
Частным случаем конуса второго порядка является круглый конус, каноническое уравнение которого имеет вид:
x2+y2-k2z2=0, где k=tga (7.3.2.)
Плоскость, параллельная плоскости Oxy, пересекает конус (7.3.2.) по окружности.
Плоскости, параллельные плоскостям Oyz и Oxz, пересекают круглый конус по гиперболам.
Замечания. 1. Не только эллипс и гипербола, но и парабола является плоским сечением круглого конуса, как например, для уравнения x2+y2-Z2=0 (при k=1), сечение конуса плоскостью, заданной уравнением x-z+1=0 есть парабола.
2. Наряду с действительными конусами второго порядка существуют ещё и мнимые конусы, которые имеют вид
![]()
7.4. Эллипсоиды и гиперболоиды
Эллипсоидом (вещественным) называется поверхность, имеющая в некоторой ("канонической" для нее) прямоугольной системе координат ("каноническое") уравнение:
![]() (7.4.1.) (рис.7.5)
(7.4.1.) (рис.7.5)

рис.7.5.
При a=b=c эллипсоид является сферой радиуса а.
Поверхность, задаваемая уравнением
![]() (7.4.2.)
(7.4.2.)
называется мнимым эллипсоидом.
Однополосным, соответственно двуполосным гиперболоидом называется поверхность, имеющая в некоторой прямоугольной системе координат уравнение
![]() -
(однополостный гиперболоид (рис.7.6.)),
(7.4.3.)
-
(однополостный гиперболоид (рис.7.6.)),
(7.4.3.)
![]() - (двуполостный гиперболоид (рис.7.7.)),
(7.4.4.)
- (двуполостный гиперболоид (рис.7.7.)),
(7.4.4.)

рис.7.6.
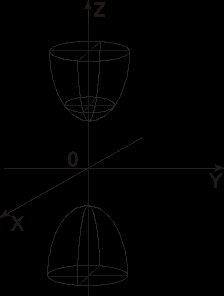
рис.7.7.
7.5. Параболоиды
Эллиптическим, соответственно гиперболическим параболоидом называется всякая поверхность, которая имеет каноническое уравнение
![]() -
для эллиптических параболоидов, (7.5.1.)
-
для эллиптических параболоидов, (7.5.1.)
![]() -для
гиперболических параболоидов, (7.5.2.)
-для
гиперболических параболоидов, (7.5.2.)
при этом p и q - положительные числа («параметры параболоидов»).
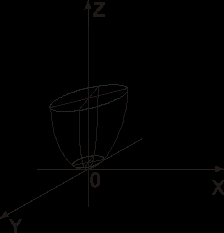
рис. 7.8.
Гиперболический параболоид представлен на рис.7.9.

рис. 7.9.
