6.4. Расстояние от точки до плоскости

Аналогично случаю прямой на плоскости, нормальное уравнение плоскости позволяет определить расстояние любой точки пространства до этой плоскости.

Теорема: Расстояние от точки M(x₀,y₀) до плоскости , данной своим нормальным уравнением (6.3.5) равно модулю числа, получаемого, если в левую часть уравнения (6.3.5) подставить x = x₀, y = y₀, z = z₀, т.е. d =x₀ cos+y₀ cos+z₀ cos-p (6.4.1)

Если плоскость  задана общим уравнением (6.1.2), то

d =Ax₀+By₀+Cz₀+D/

6.5. Взаимное расположение двух плоскостей

Пересекающиеся плоскости A₁x + B₁y + C₁z + D₁ = 0 (6.5.1)

и A₂x + B₂y + C₂z + D₂ = 0 (6.5.2)

образуют две пары вертикальных двугранных углов.

Углом между плоскостями будем называть любой из двух смежных двугранных углов. Один из них равен углу  между векторами (A₁, B₁, C₁) и (A₂, B₂, C₂), перпендикулярными соответственно к плоскостям (6.5.1) и (6.5.2), а второй - ₁=180⁰-. Следовательно искомый угол можно найти по формуле: ( , )=  cos 

(6.5.3)

Если плоскости параллельны, то угол  между ними равен 0 или , отсюда следует, что и коллинеарны и мы получим условие параллельности двух плоскостей

A₁/A₂ = B₁/B₂ = C₁/C₂ (6.5.4)

Если, то из формулы (6.5.3) получим условие перпендикулярности двух прямых

A₁A₂ + B₁B₂ + C₁C₂ = 0 (6.5.5)

Замечание: Если выполняется условие A₁/A₂=B₁/B₂=C₁/C₂=D₁/D_2, то плоскости совпадают.

6.6. Пучок плоскостей

Пучком плоскостей называется совокупность всех плоскостей, проходящих через одну и ту же прямую. Уравнение пучка плоскостей имеет вид:

(A₁x + B₁y + C₁z + D₁) + (A₂x + B₂y + C₂z + D₂) = 0,

где  - действительный параметр.

Уравнением пучка плоскостей удобно пользоваться при решении многих задач аналитической геометрии.

Примеры:

1. Найти уравнение плоскости, проходящей через линию пересечения плоскостей x + y - z - 2 = 0 и 2x - 3y + z - 7 = 0 и через точку M₀(1; 3; -2).

Решение. Искомая плоскость принадлежит пучку x + y - z - 2 + (2x - 3y + z - 7) = 0

Параметр  находим из условия, что точка М₀ лежит на искомой плоскости:

1 + 3 - ( - 2) + (2*1-3*3 - 2 - 7)=0   = 1/4

Уравнение плоскости имеет вид: x + y - z - 2 + 1/4(2x - 3y + z - 7) = 0, после упрощений уравнение плоскости имеет вид: 6x + y - 3z - 15 = 0.

2. Найти уравнение плоскости, проходящий через линию пересечения плоскостей 2x + y - z = 0 и 2y + z - 2 = 0 и перпендикулярной к плоскости x + 3y + z = 0

Решение. Искомая плоскость принадлежит пучку 2x + y - z + (2y + z - 2) = 0

Используя условие перпендикулярности двух плоскостей (6.5.5), имеем:

A₁ = 2, B₁ = (1 + 2), C₁ = (-1 + )

A₂ = 1, B₂ = 3, C₂ = 1

A₁A₂ + B₁B₂ + C₁C₂ = 0  2 + 3(1 + 2) + ( - 1) = 0   = -4/7

Уравнение плоскости имеет вид: 14x - y - 11z + 8 = 0

6.7. Уравнение плоскости, проходящей через три заданные точки

Пусть заданы три точки M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃), относительно которых мы будем предполагать, что они не лежат на одной прямой. Найдём уравнение плоскости проходящей через эти три точки.

П усть M(x,y,z) – произвольная точка искомой плоскости (рис. 6.3) .

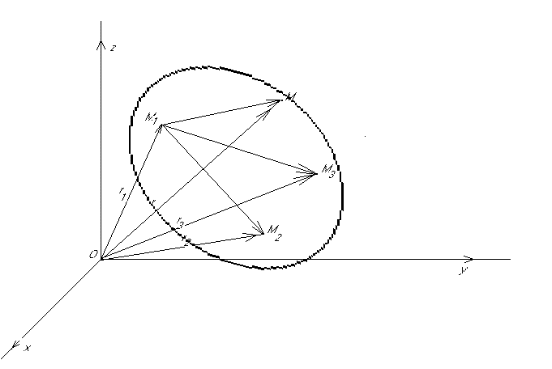
Рис. 6.3

Векторы = - , = - , = - лежат в искомой плоскости и поэтому компланарны (условие компланарности устанавливается с помощью смешанного произведения).

Из компланарности векторов , и и перехода к координатной форме записи, ( (x - x₁, y - y₁, z - z₁); (x₂ - x₁, y₂ - y₁, z₂ - z₁); (x₃-x₁, y₃-y₁, z₃-z₁)), получим уравнение плоскости в координатной форме, проходящей через три точки:

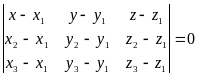(6.7.1)