8.5. Построение точек пересечения прямой с поверхностью многогранника

Построение точек пересечения пря­мой с поверхностью многогранника сводится к построению линии пересе­чения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рисунке 8.11 приведено постро­ение проекций e', e и f', f точек пересечения прямой с проекци­ями m'n', mn с боковыми гранями пирамиды. Пирамида задана проекциями s', s вершины и a'b'c', abc основания. Прямая MN заключена во вспомогательную фронтально-проецирующую плос­кость T(T_v). Горизонтальные проекции e и f искомых точек по­строены в пересечении проекции mn с горизонтальными проекциями 1–2 и 2–3 отрезков, по которым плоскость T пересекает боковые грани пирамиды. Фронтальные проекции e' и f' определены по линиям связи.

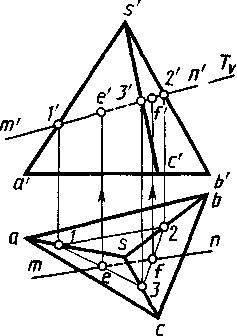
Рис.8.11

8.6. Взаимное пересечение многогранников

Изображение пересекающихся между собой в пространстве призмы А и пирамиды Б представлено на рисунке 8.12. Линия их пересечения проходит через точки 1, 3, 4, 6 пересечения ребер пирамиды с гранями призмы и точки 2, 5 пересечения ребра призмы с гранями пирамиды. В общем случае в пересе­чении многогранников получается пространственная замкну­тая ломаная линия, которая в некоторых частных случаях может оказаться плоской.

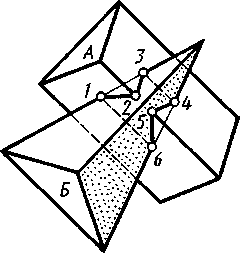
Рис.8.12

При построении линии пересечения многогранников при­меняют два способа и их комбинации.

1. Строят точки пересечения ребер одного многогранника с гра­нями другого и ребер второго с гранями первого. Через построенные точки в определенной последовательнос­ти приводят ломаную линию пересече­ния данных многогранников. При этом отрезки прямых проводят лишь через те построенные точки, которые лежат в одной и той же грани.

2. Строят отрезки прямых, по ко­торым грани одной поверхности пере­секают грани другой. Эти отрезки являются звеньями ломаной линии пересечения многогранных поверхно­стей между собой.

Таким образом, построение линии пересечения двух мно­гогранников сводится или к построению линии пересечения двух плоскостей между собой, или к построению точки пере­сечения прямой с плоскостью. Обе эти задачи рассмотрены выше. На практике обычно используют оба способа в комби­нации, исходя из условия простоты и удобства построения.

В качестве примера рассмотрим построение линии пересе­чения усеченной правильной четырехугольной пирамиды и на­клонно расположенной трехгранной призмы (рис. 8.13, а). Прежде чем приступить к построениям, анализируют взаим­ное положение многогранников и их расположение относительно плоскостей проекций. В данном случае очевидно, что много­гранники могут пересекаться только по боковым граням. Реб­ра призмы и боковые ребра пирамиды параллельны плоскости V, основания пирамиды параллельны плоскости H. Нижняя грань призмы и ее основания перпендикулярны плоскости V.

Указанные особенности расположения призмы и пирамиды определяют и наиболее рациональный способ построения ли­нии пересечения их поверхностей по точкам пересечения ребер призмы с гранями пирамиды и боковых ребер пирамиды с гра­нями призмы.

Построения показаны на рисунке 6.13, б. Рассмотрим их для левой части чертежа (от оси пирамиды). Проекции 1', 1, 2', 2, 3,' 3, 4', 4 точек пересечения ребер призмы с гранями пирамиды найдены путем проведения через них фронтальных плоскостей Q (Q_h), P (P_h), T (T_h). Они пересекают левые боковые грани пирамиды по фронталям – прямым линиям, параллельным левому ребру пирамиды. Положение их фрон­тальных проекций определено по горизонтальным проекциям 21, 22 и 24 точек пересечения горизонтальных проекций Q_h, P_h и T_h плоскостей Q, P, T с горизонтальной проекци­ей основания пирамиды. В пересечении фронтальных про­екций этих линий с фронтальными проекциями ребер призмы найдены фронтальные проекции 1',2' и 4' точек пересече­ния ребер призмы с левыми гранями пирамиды. По ним по­строены горизонтальные проекции 1, 2, 4.