7.3. Поверхности и тела вращения

Поверхности вращения и ограничиваемые ими тела имеют широкое применение во многих областях техники:

• баллон элек­тронно-лучевой трубки (рис. 7.11, а),

• центр токарного станка (рис.7.11, б),

• объемный СВЧ резонатор элек­тромагнитных колебаний (рис.7.11, в),

• сосуд Дьюара для хра­нения жидкого воздуха (рис. 7.11, г),

• коллектор электронов мощного электронно-лучевого прибора (рис. 7.11, д) и т.д.

В зависимости от вида образующей поверхности вращения могут быть ли­нейчатыми, нелинейчатыми или состо­ять из частей таких поверхностей.

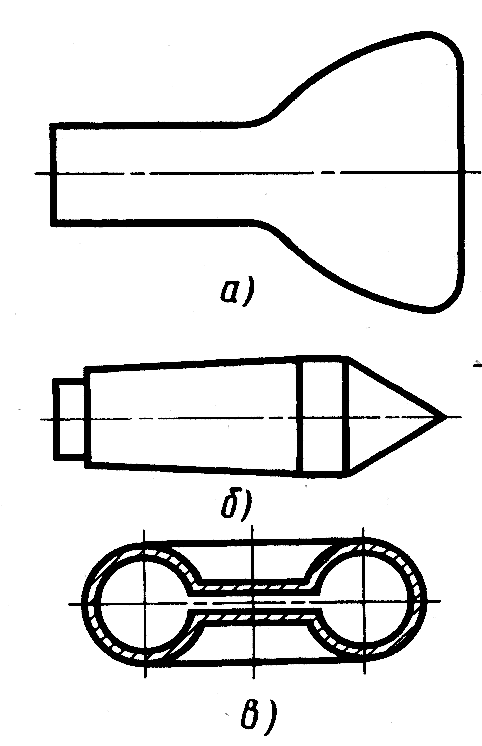
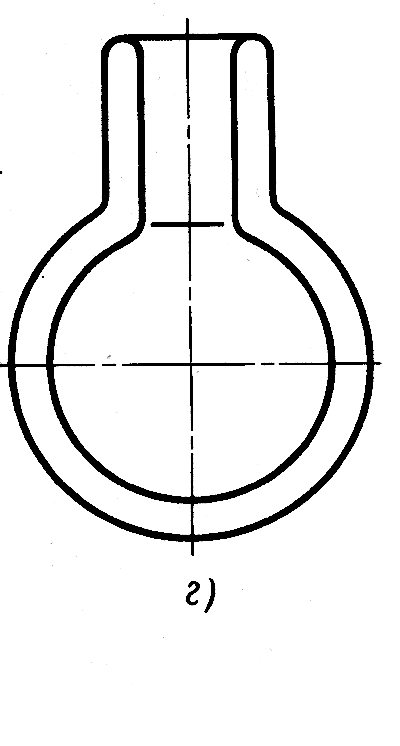
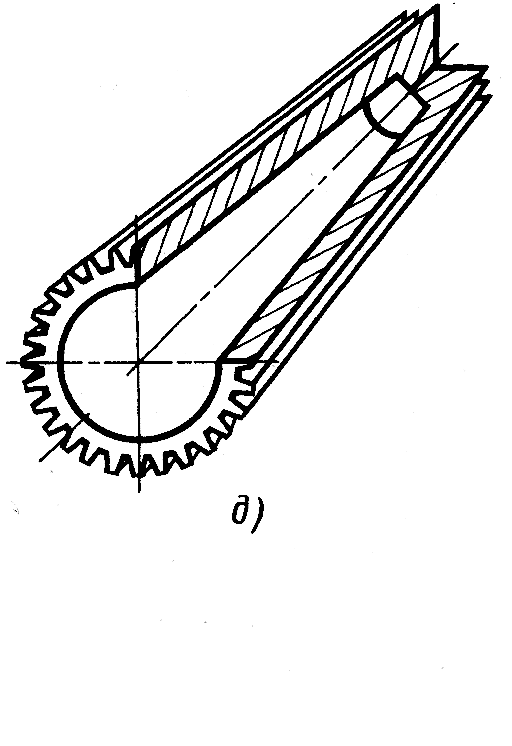
Рис.7.11

Поверхностью вращения называют поверхность, получающуюся от враще­ния некоторой образующей линии вокруг неподвижной прямой – оси поверхности. На чертежах ось изображают штрихпунктирной линией. Образующая линия может в общем случае иметь как кри­волинейные, так и прямолинейные участки. Поверхность вращения на чер­теже можно задать образующей и по­ложением оси.

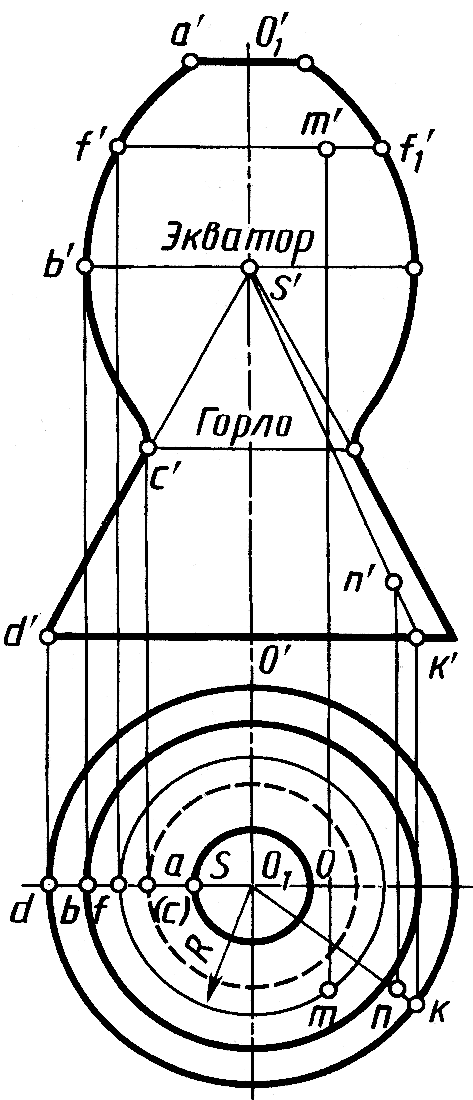
На рисунке 7.12 изоб­ражена поверхность вращения, которая образована вращением образующей ABCD (ее фронтальная проекция a'b'c'd') вокруг оси OO₁ (фронталь­ная проекция o'o₁), перпендикулярной плоскости H.

При вращении каждая точка образующей описывает окруж­ность, плоскость которой перпендику­лярна оси. Соответственно линия пересечения поверхности вра­щения любой плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями. На виде сверху (рис. 7.12) показаны проекции окружностей, опи­сываемых точками А, В, С и D, проходящие через проекции a, b, с, d. Наибольшую параллель из двух соседних с нею параллелей по обе стороны от нее называют экватором, анало­гично наименьшую – горлом.

Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхно­стью вращения – меридианом. Если ось поверхности параллельна плоскости проекций, то меридиан, лежащий в плоскости, параллельной этой плоскости проекций, называют главным меридианом. На эту плоскость проекций главный меридиан проецируется без искажений. Так, если ось поверхности вра­щения параллельна плоскости V, то главный меридиан про­ецируется на плоскость V без искажений, например проекция a'f'b'c'd'. Если ось поверхности вращения

Рис.7.12 перпендикулярна к плоскости H, то горизонтальная проекция

поверхности име­ет очерк в виде окружности.

Наиболее удобными для выполнения изображений поверх­ностей вращения являются случаи, когда их оси перпендику­лярны к плоскости H, к плоскости V или к плоскости W.

Некоторые поверхности вращения являются частными слу­чаями поверхностей, рассмотренных в 7.1, например цилиндр вращения, конус вращения. Для цилиндра и конуса вращения меридианами являются прямые линии. Они параллельны оси и равноудалены от нее для цилиндра или пересекают ось в од­ной и той же ее точке под одним и тем же углом к оси для конуса. Цилиндр и конус вращения – поверхности, беско­нечные в направлении их образующих; поэтому на изображе­ниях их ограничивают какими-либо линиями, например линиями пересечения этих поверхностей с плоскостями проек­ций или какими-либо из параллелей. Из стереометрии извест­но, что прямой круговой цилиндр и прямой круговой конус ограничены поверхностью вращения и плоскостями, перпен­дикулярными к оси поверхности. Меридиан такого цилинд­ра – прямоугольник, конуса – треугольник.

Такая поверхность вращения, как сфера, является ограни­ченной и может быть изображена на чертеже полностью. Эква­тор и меридианы сферы – равные между собой окружности. При ортогональном проецировании на все три плоскости про­екций очертания сферы проецируются в окружность.

Тор. При вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, получается поверхность с названием тор. На ри­сунке 7.13 приведены:

• открытый тор, или круговое кольцо, – рисунок 7.13, а,

• закрытый тор – рисунок 7.13, б,

• самопересека­ющийся тор – рисунок 7.13, в, г. Тор (рис. 7.13, г) называют также лимоновидным.

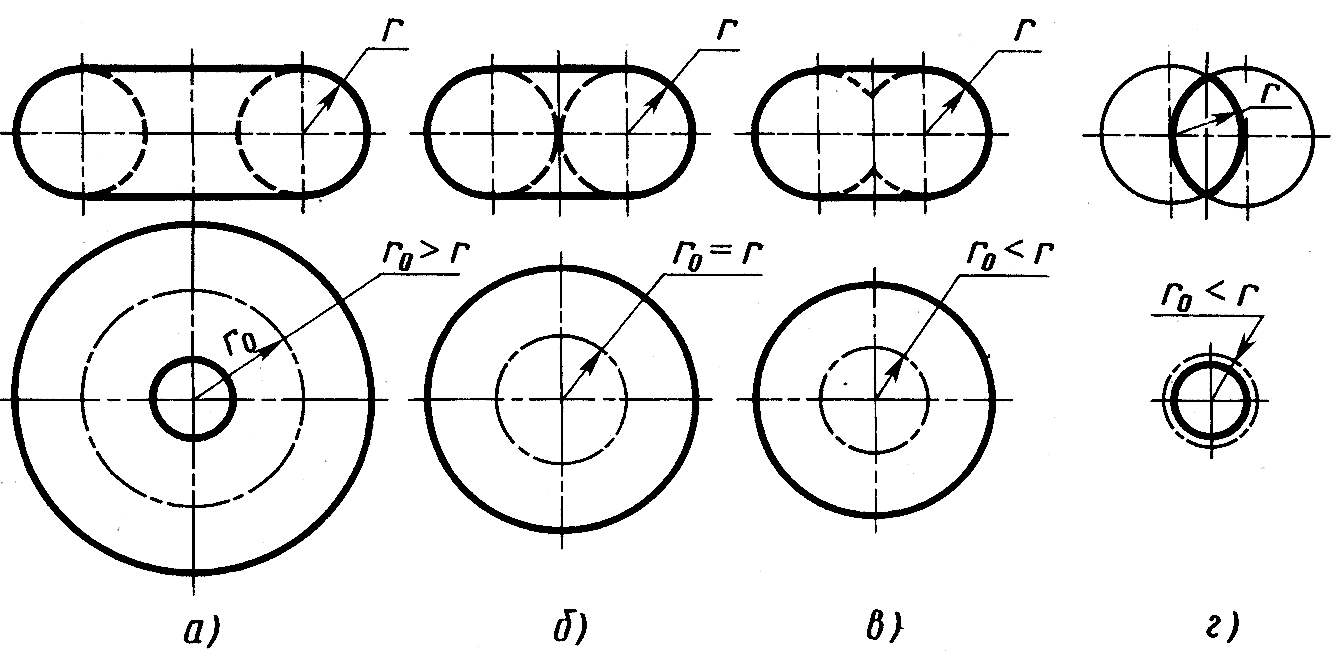
Рис.7.13

На рисунке 7.13 они изображены в по­ложении, когда ось тора перпендикулярна к плоскости про­екций H. В открытый и закрытый торы могут быть вписаны сферы. Тор можно рассматривать как поверхность, огибаю­щую одинаковые сферы, центры которых находятся на ок­ружности.

В построениях на чертежах широко используют две системы круговых сечений тора: в плоскостях, перпендикулярных к его оси, и в плоскостях, проходящих через ось тора. При этом в плоскостях, перпендикулярных к оси тора, в свою очередь имеются два семейства окружностей – линий пересечения плоскостей с наружной поверхностью тора и линий пересечения плоскостей с внутренней поверхностью тора

У лимоновидного тора (рис. 8.13, г) имеется только первое семейство окружностей.

Кроме того, тор имеет еще и третью систему круговых сече­ний, которые лежат в плоскостях, проходящих через центр тора и касательных к его внутренней поверхности. На рисунке 7.14 показаны круговые сечения с центрами о_1p и о_2р на дополни­тельной плоскости проекций P, образованные фронтально-про­ецирующей плоскостью Q (Q_v), проходящей через центр тора с проекциями о' о и касательной к внутренней поверхности тора в точках с проекциями 1', 1, 2', 2. Проекции точек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 облегчают чтение чертежа. Диаметр d этих круговых сечений равен длине больших осей эллипсов, в которые проецируются круговые сечения на горизонтальной плоскости проекций: d = 2R.

Рис.7.15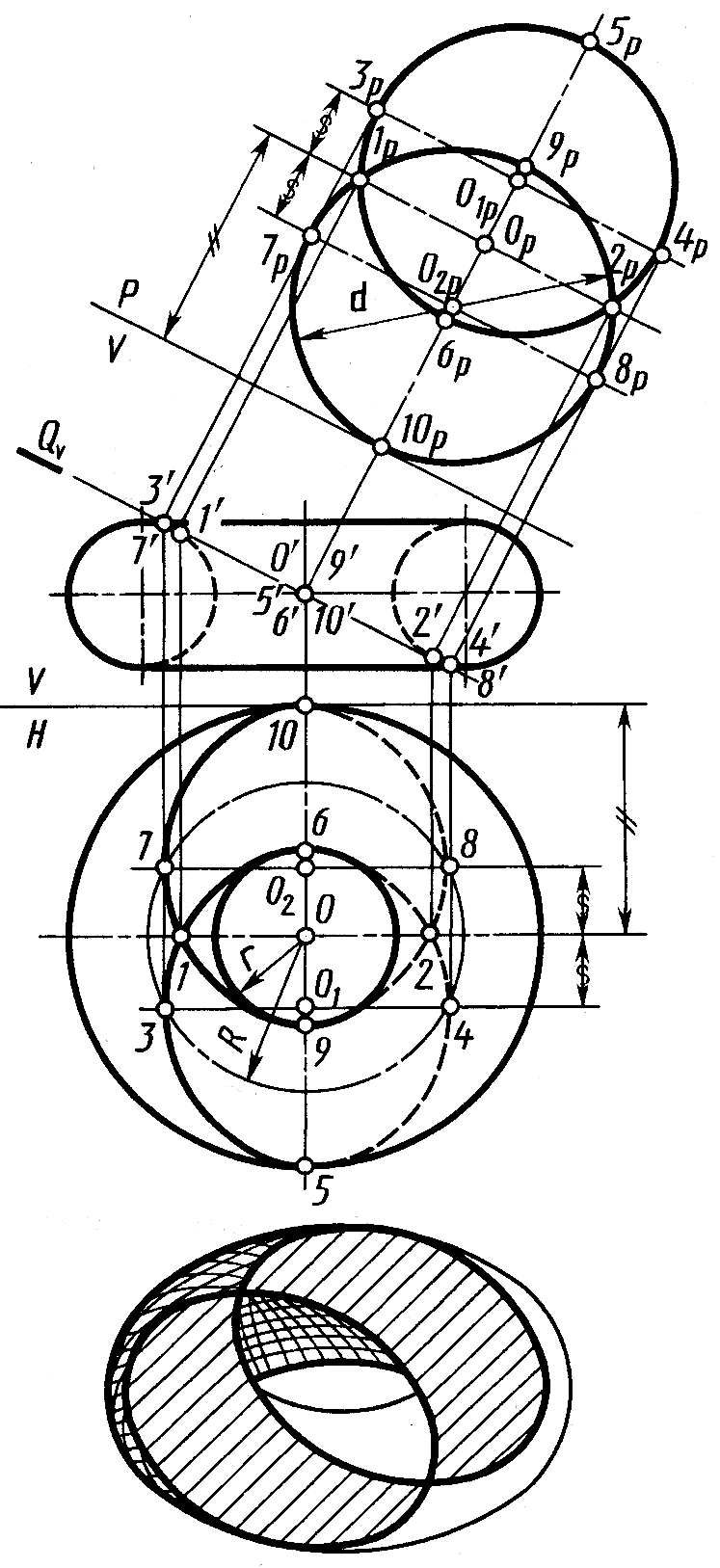

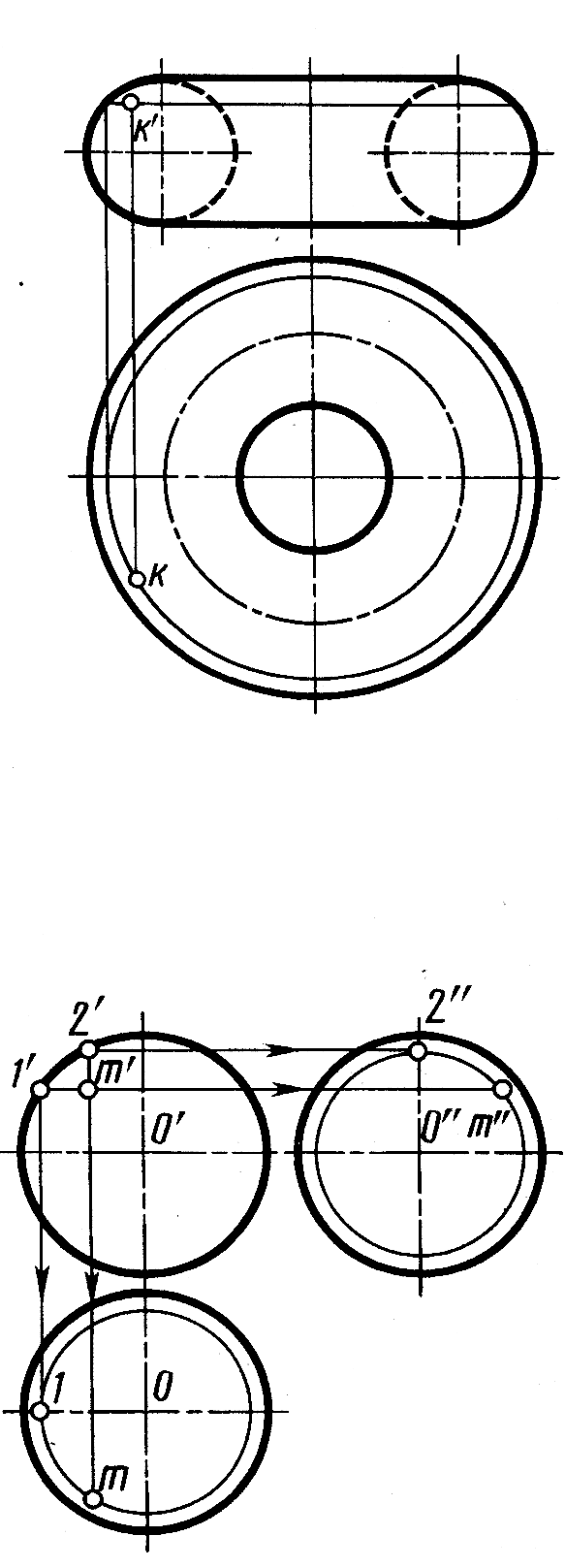
Рис.7.14 Рис.7.16

Точки на поверхности вращения. Положение точки на по­верхности вращения определяют по принадлежности точки ли­нии каркаса поверхности, т. е. с помощью окружности, проходящей через эту точку на поверхности вращения. В слу­чае линейчатых поверхностей для этой цели возможно приме­нение и прямолинейных образующих.

Применение параллели и прямолинейной образующей для построения проекций точек, принадлежащих данной поверхности вращения, показано на рисунке 7.12. Если дана проекция m' то проводят фронтальную проекцию f'f'₁ параллели, а затем радиусом R проводят окружность – го­ризонтальную проекцию параллели – и на ней находят проекцию m. Если бы была задана горизонтальная проек­ция m, то следовало бы провести радиусом

R = om окруж­ность, по точке f построить f' и провести f''f'₁ – фронтальную проекцию параллели – и на ней в проекционной связи отметить точку m'. Если дана проекция n' на линейчатом (коническом) участке поверхности вращения, то проводят фронтальную проекцию d's' очерковой образу­ющей и через проекцию n' – фронтальную проекцию s'k' образующей на поверхности конуса. Затем на горизонталь­ной проекции sk этой образующей строят проекцию п. Если бы была задана горизонтальная проекция n, то сле­довало бы провести через нее горизонтальную проекцию sk образующей, по проекции k' и s' (построение ее было рассмотрено выше) построить фронтальную проекцию s'k' и на ней в проекционной связи отметить проекцию n'.

На рисунке 7.15 показано построение проекций точки К, принадлежащей поверхности

тора. Следует отметить, что по­строение выполнено для видимых горизонтальной проекции к и фронтальной проекции k'.

На рисунке 7.16 показано построение по заданной фрон­тальной проекции m' точки на поверхности сферы ее гори­зонтальной m и профильной m''проекций. Проекция m построена с помощью окружности – параллели, проходящей через проекцию m'. Ее радиус – o–1. Проекция m" построена с помощью окружности, плоскость которой параллельна профильной плоскости проекций, проходящей через проек­цию m'. Ее радиус o"2".

Построение проекций линий на поверхности вращения мо­жет быть выполнено также при помощи окружностей – па­раллелей, проходящих через точки, принадлежащие этой линии.

На рисунке 7.17 показано построение горизонтальной про­екции ab линии, заданной фронтальной проекцией a'b' на по­верхности вращения, состоящей из частей поверхностей сферы, тора, конической. Для более точного вычерчивания горизон­тальной проекции линии продолжим ее фронтальную проек­цию вверх и вниз и отметим проекции 6' и 5' крайних точек. Горизонтальные проекции 6, 1, 3, 4, 5 построены с помощью линий связи. Проекции b, 2, 7, 8, а построены с помощью параллелей, фронтальные проекции которых проходят через проекции b', 2' 7', 8' a' этих точек. Количество и располо­жение промежуточных точек выбирают исходя из формы ли­нии и требуемой точности построения. Горизонтальная проекция линии состоит из участков: b –1 – части эллипса, 3 – 8 – a – 4 – части эллипса,

1 – 2 – 7 – 3 – кривой четвертого порядка (проекция кривой на поверхности тора).

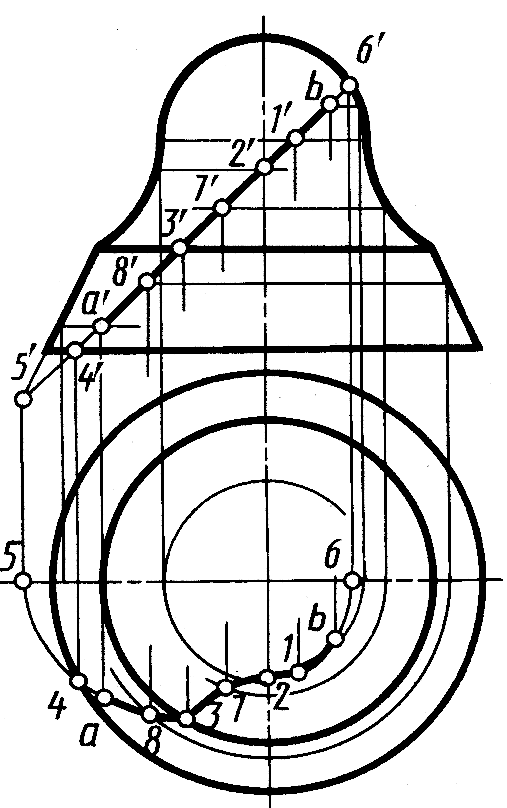
Рис. 7.17

Контрольные вопросы к главе 7.

1. Что такое поверхность?

2. Что такое образующая (или производящая) линия поверхности?

3. В чем различие между линейчатой и нелинейчатой поверхностями?

4. Как образуются прямая и наклонная винтовые поверхности?

1. По каким линиям пересекает прямую и косую винтовые поверхно­сти плоскость, перпендикулярная к оси поверхности?

5. Что называют поверхностью вращения?

6. Что называют параллелями и меридианами на поверхности вра­щения, экватором, горлом, главным меридианом?

7. Как образуется поверхность, называемая тором?

8. В каком сечении открытого тора получаются две одинаковые ок­ружности?

10. Сколько систем круговых сечений имеет тор?

11. Как определяют положение точек на поверхности вращения?