3.4 Максимально правдоподобная оценка

Из анализа байесовских оценок следует, что для получения оптимальных оценок требуется знание после опытных плотностей распределения вероятностей измеряемого параметра α. По теореме умножения плотность распределения вероятностей совмещения событий p(α,х) может быть представлена в двух видах:

p(α,х)=p(х)p(α/х)=p(α)p(х/α) (3.13)

Пользуясь этим равенством, можно установить связь после опытной плотности вероятностей p(α/х) с безусловной до опытной плотностью распределения измеряемого параметра p(α) и условной плотностью вероятности принятой реализации при измеренном значении параметра p(х/α):

p(α/x)= p(α)p(x/α) (3.14)

Стоящая в знаменателе равенства (3.14) безусловная плотность вероятностей реализации х, содержащей любое значение α, может быть определена, как:

p(x)= (3.15)

С учетом (3.15) и (3.14) может быть записана в виде:

p(α/x)=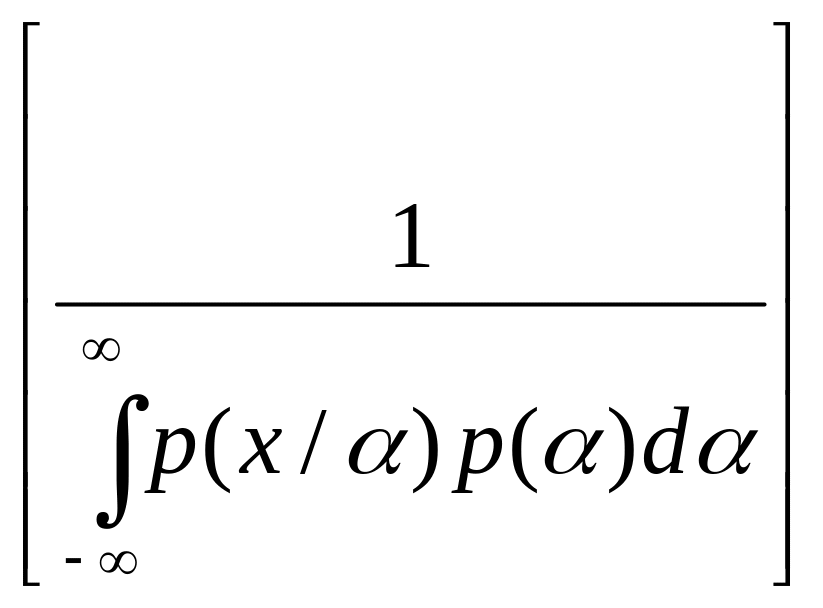 p(α)p(х/α),

где не зависящий от α знаменатель играет роль нормирующего множителя

N=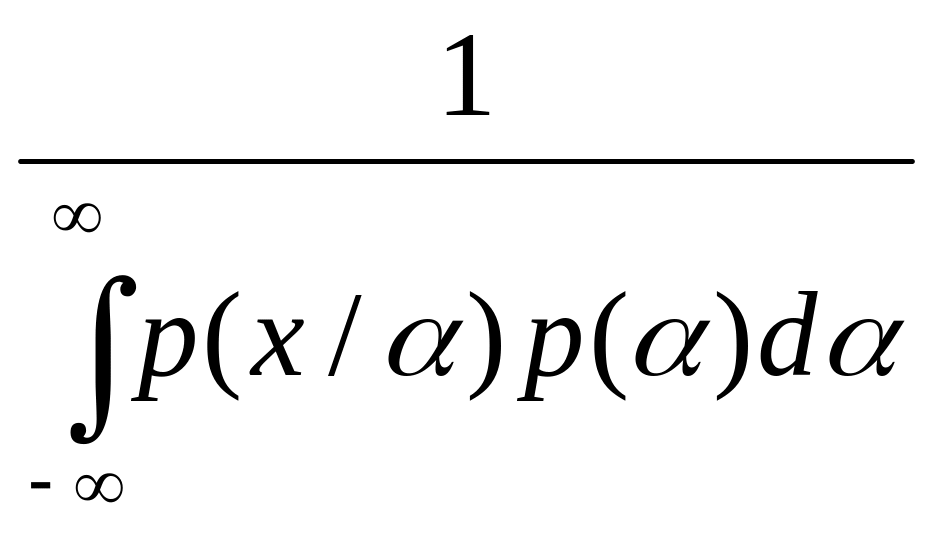 , т.е.

p(α/x)=Np(α)p(x/α) (3.16)

По аналогии с теорией обнаружения можно ввести условное отношение правдоподобия как отношение условий плотности вероятностей реализации при наличии сигнала, содержащего параметр α, к плотности вероятностей реализации, содержащей только помеху:

l(x/α) = (3.17)

С учетом (3.17) выражение (3.16) может быть переписано в виде:

p(α/x)=N’p(α)l(x/α), (3.18)

где N’= -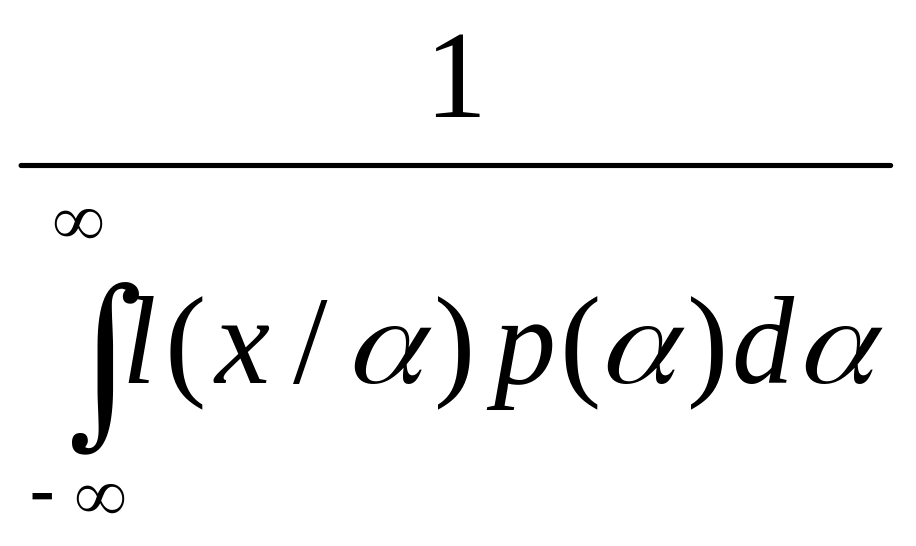

множитель, как и N, нормирующий площадь под кривой послеопытной плотности вероятностей к единице. Таким образом, методика отыскания оптимальных оценок α*_опт сводится к определению функций, пропорциональных послеопытной плотности вероятностей параметра α, и определению абсциссы максимума этих функций. При этом существенное влияние на послеопытное распределение оказывает уровень помех.

Рассмотрим влияние помех на простейшем примере оптимизации измерения параметра с равномерной плотностью распределения в интервале α₁<α<α₂:

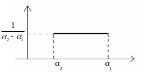
Распределение помехи считаем центрированным гауссовским:

p_n(x)

-x

x

Тогда условная плотность вероятностей при измеренном значении α

Соответствующая после опытная плотность распределения вероятностей на основе равенства (3.16) p(x/α)=Np(α)p(x/α)

α₂

α₁

α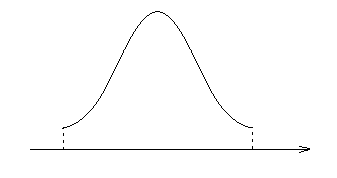

Кривая p(α/x), таким образом учитывает как результат измерения х, так и доопытные данные о распределении измеряемой величины α и помехи n(t). Влияние соотношения сигнал/помеха на результат измерения можно проиллюстрировать рисунком для двух крайних случаев – слабой и сильной помехи.

Пусть помеха мала (σ_n<<α ₂ –α₁)

p(α/x) p(x/α)

α₁

α₂

α

При сильной помехе (σ_n>>α ₂ –α₁)

p(х/α)

p(α/x)≈p(α)

α₁

α₂

α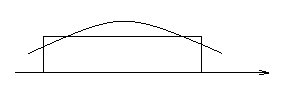

В первом случае (при высокочастотных измерениях) нет необходимости в знании доопытного распределения p(α), и ход кривой послеопытного распределения определяется измерением х и дисперсией помехи σ_n. Во втором случае кривые послеопытного распределения не отличается от доопытного, т.е. результаты измерения не достоверны. Таким образом, в случае высокоточных измерений, т.е. когда распределение p(α) значительно шире p(х/α), доопытная информация не уточняет результаты измерений, и отыскание оптимальной оценки сводится к оценке максимального правдоподобия, соответствующей абсциссе максимума одной из монотонно связанных между собой функций: p(х/α), l(x/α), lnl(x/α). Последняя функция часто удобна, т.к. для ряда законов распределения сводится к какой-либо простой функции измеряемого параметра α, получаемого на выходе оптимального устройства обнаружения до пороговой схемы.

В случае измерения параметров ₁ , ₂,… _n оптимизация оценки сводится к решению уравнений правдоподобия

; ; … .

Следует отметить, что если ошибки измерения распределены по гауссовскому закону, то метод максимального правдоподобия дает те же результаты, что и классический способ обработки статистических измерений по методу наименьших квадратов.

Ранее мы показали, что отношение правдоподобия монотонно связано с корреляционным интегралом. Тогда оптимальную оценку можно находить из условия:

,

где Z(x/α) – корреляционный интеграл при значении параметра, равном α. Это – оптимальная оценка по критерию максимума правдоподобия.

Реализация оптимальной оценки требует вычисления множества значений корреляционного интеграла. Следовательно, нужно иметь многоканальные корреляторы, каждый канал которых вычисляет корреляционный интеграл Z(x/α) при фиксированном значении параметра. Практически число каналов ограничивается конечностью интервалов неопределенности по τ и Ω для функций неопределенности реальных зондирующих сигналов. Если у нас используются не корреляторы, а согласованные фильтры, то каждый канал все равно нужно стробировать по времени, и согласованные фильтры ставятся уже после стробирующего устройства.

Схема корреляционного интеграла имеет вид:

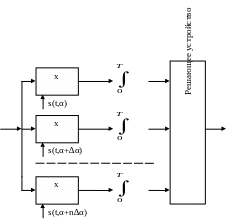
На перемножитель подаются копии сигналов, причем значение измеряемого параметра в каждом канале свое, изменяющееся с шагом ∆α. Максиму будет в i-том канале, в котором α+(i-1)∆α ближе всего к измеряемому. Решающее устройство выбирает канал с максимальным значением корреляционного интеграла, и соответствующее значение параметра приписывается измеряемому параметру.