
- •3. Статистические методы оценки параметров сигналов.
- •3.1 Понятие об оценке параметров принимаемых сигналов.
- •3.2 Качество оценок и критерии оптимальности измерения параметров.
- •3.3 Основные положения байесовской теории измерений
- •3.4 Максимально правдоподобная оценка
- •3.5 Потенциальная точность определения параметра
- •3.6 Потенциальная точность определения момента прихода сигнала
- •3.7 Потенциальная точность определения доплеровского сдвига частоты.
- •4. Пространственно временная обработка сигналов.
- •4.1 Пространственно-временной сигнал.
- •4.2 Случайные пространственно-временные сигнала
- •4.3 Случайные поля и пространственные фильтры
- •4.4 Линейная фильтрация стационарных пространственно-временных сигналов
- •5. Основы цифровой обработки сигналов.
- •5.1 Модели дискретных сигналов
- •5.2 Дискретизация периодических сигналов
- •5.3 Основы теории z-преобразования
- •5.4 Цифровые фильтры
- •5.5 Трансверсальные цифровые фильтры
- •5.6 Рекурсивные цифровые фильтры
- •5.7 Основы гомоморфной обработки сигналов
- •5.8 Гомоморфная обработка мультипликативного сигнала
- •5.9 Гомоморфная обработка свернутого сигнала
- •5.9 Кепстральный анализ сигналов
5.3 Основы теории z-преобразования
При анализе и синтезе дискретных и цифровых устройств широко используют так называемое Z-преобразование, играющее по отношению к дискретным сигналам такую же роль, как интегральные преобразования Фурье и Лапласа по отношению к непрерывным сигналам. Рассмотрим основы этого преобразования.
Пусть {хk}=(х0,х1,х2…) – числовая последовательность, конечная или бесконечная, содержащая отсчетные значения некоторого сигнала. поставим ей в соответствие сумму ряда по отрицательным степеням комплексной переменной z:
![]() (5.17)
(5.17)
Назовем эту сумму, если она существует, Z-преобразованием последовательности {хk}.
На основании (5.17) можно непосредственно найти Z-преобразования дискретных сигналов с конечным числом отсчетом. Так, простейшему дискретному сигналу с единичным отсчетом {хk}=(1,0,0…) соответствует X(z)=1. Если же, например, {хk}=(1,1,1,0,0,0…), то
![]()
Если же в ряде (5.17) число слагаемых
бесконечно велико, то необходимо
исследовать его сходимость. Пусть
коэффициенты рассматриваемого ряда
удовлетворяют условию
![]() при любых k≥0. Здесь M>0,
R0>0 – постоянные
вещественные числа. Тогда в теории
функций комплексного переменного
показано, что ряд (5.17) сходится при всех
значениях z, таких, что
│z│>R0.
В этой области сходимости сумма ряда
представляет собой аналитическую
функцию переменных z, не
имеющую ни полюсов, ни существенно
особых точек. Рассмотрим, например,
дискретный сигнал {хk}=(1,1,1,…),
образованный одинаковыми единичными
отсчетами и служащий моделью обычной
функции включения. Бесконечный ряд
при любых k≥0. Здесь M>0,
R0>0 – постоянные
вещественные числа. Тогда в теории
функций комплексного переменного
показано, что ряд (5.17) сходится при всех
значениях z, таких, что
│z│>R0.
В этой области сходимости сумма ряда
представляет собой аналитическую
функцию переменных z, не
имеющую ни полюсов, ни существенно
особых точек. Рассмотрим, например,
дискретный сигнал {хk}=(1,1,1,…),
образованный одинаковыми единичными
отсчетами и служащий моделью обычной
функции включения. Бесконечный ряд
![]() является суммой геометрической прогрессии
и сходится при любых z в
кольце │z│>1. суммируя
прогрессию, получаем:
является суммой геометрической прогрессии
и сходится при любых z в
кольце │z│>1. суммируя
прогрессию, получаем:
![]()
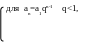
На границе области аналитичности при z=1 эта функция имеет единственный простой полюс. Аналогично получается Z-преобразование бесконечного дискретного сигнала {хk}=(1,а,а2,…), где а – некоторое вещественное число. Здесь:
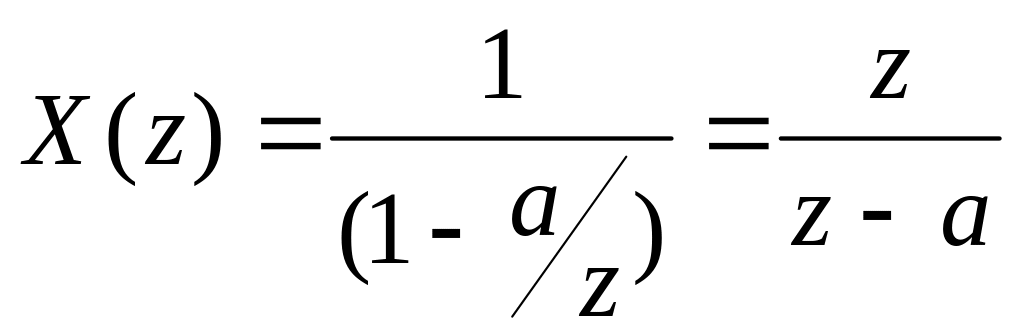
Данное выражение имеет смысл в кольцевой области │z│>а.
Z-преобразование можно применить и к непрерывным функциям. Пусть отсчеты {хk} есть значения непрерывной функции х(t) в точках t=k∆. Тогда любому сигналу х(t) можно сопоставить его Z-преобразование при любом шаге дискретизации:
![]() (5.18)
(5.18)
Например, если x(t)=exp(αt), то соответствующее Z-преобразование:
![]()
является аналитической функцией при │z│>ехр(α∆).
Пусть Х(z) – функция комплексной переменной z, аналитическая в кольцевой области │z│>R0. замечательное свойство Z-преобразования состоит в том, что функция X(z) определяет всю бесконечную совокупность отсчетов (х0,х1,х2…).
Действительно, умножим обе части ряда (5.17) на множитель zm-1:
![]() (5.19),
(5.19),
а затем вычислим интегралы от обеих частей
полученного равенства, взяв в качестве
контура произвольную замкнутую кривую,
лежащую целиком в области аналитичности
и охватывающую все полюсы функции Х(z).
При этом воспользуемся фундаментальным
положением, вытекающим их теоремы Коши:
затем вычислим интегралы от обеих частей
полученного равенства, взяв в качестве
контура произвольную замкнутую кривую,
лежащую целиком в области аналитичности
и охватывающую все полюсы функции Х(z).
При этом воспользуемся фундаментальным
положением, вытекающим их теоремы Коши:
![]()
Очевидно, интегралы от всех слагаемых в правой части обратятся в нуль, за исключением слагаемого с номером m, поэтому
![]() (5.20)
(5.20)
Данное выражение называется обратным сZ-преобразованием. Определим при t≥0 Сигнал вида идеальной МИП:
![]()
Преобразовав его по Лапласу, получим изображение:
![]() ,
,
которое непосредственно переходит в Z-преобразование, если выполнить подстановку Z=exp(p∆). Если же положить Z=exp(jω∆), то выражение
![]()
будет преобразованием Фурье импульсной последовательности.
Рассмотрим некоторые свойства Z-преобразования.
1. Линейность. Если {хk} и {yk} – некоторые дискретные сигналы, причем известны соответствующие Z-преобразования X(z) и Y(z), то сигналу {uk}={α хk+β yk} будет отвечать преобразование U(z)=αX(z)+βY(z) при любых постоянных α и β.
2. Z-преобразование смещенного сигнала. Рассмотрим дискретный сигнал {yk}, получающий при сдвиге дискретного сигнала {хk} на одну позицию в сторону запаздывания. Непосредственно вычисляя Z-преобразование, получаем следующий результат:
![]() (k=n+1)
(k=n+1)
Таким образом, символ
![]() служит оператором единичной задержки
(на один интервал дискретизации) в
Z-области.
служит оператором единичной задержки
(на один интервал дискретизации) в
Z-области.
3. Z-преобразование свертки. Пусть x(t) и y(t) – непрерывные сигналы, для которых определена свертка:
![]()
Применительно к дискретным сигналам по аналогии с этим принято вводить дискретную свертку {fk} – последовательность чисел, общий член которой:
![]() ,
m=0,1,2…
(5.21)
,
m=0,1,2…
(5.21)
Вычислим Z-преобразование дискретной свертки:
![]() (5.22)
(5.22)
Итак, свертка двух дискретных сигналов отвечает произведение Z-преобразований.
