5.2 Дискретизация периодических сигналов

Модель дискретного сигнала вида (5.1) предполагает, что отсчетные значения аналогового сигнала х(t) могут быть получены в неограниченном числе точек на оси времени. Практически это невозможно, обработка всегда ведется на конечном интервале времени. Изучим особенности спектрального представления дискретного сигнала, который задан на отрезке [0,T] своими отсчетами х₀,х₁,х₂…х_N-1, взятыми соответственно в моменты времени 0,∆,2∆,…(N-1)∆. Полное число отсчетов N=T/∆. Массив этих чисел, вещественных или комплексных, является единственным источником сведений о спектральных свойствах сигнала х(t).

Методика изучения таких дискретных сигналов состоит в том, что полученная выборка отсчетных значений мысленно повторяется бесконечное число раз. В результате сигнал становится периодическим. Сопоставив такому сигналу некоторую математическую модель, можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты. Совокупность этих коэффициентов образует спектр дискретного периодического сигнала.

Сопоставим исходному колебанию х(t) его представление в виде МИП:

(5.8)

Представим (5.8) в виде комплексного ряда Фурье:

(5.9)

с коэффициентами

Подставив сюда (5.8) и введя безразмерную переменную ξ=t/∆, получим:

(5.10)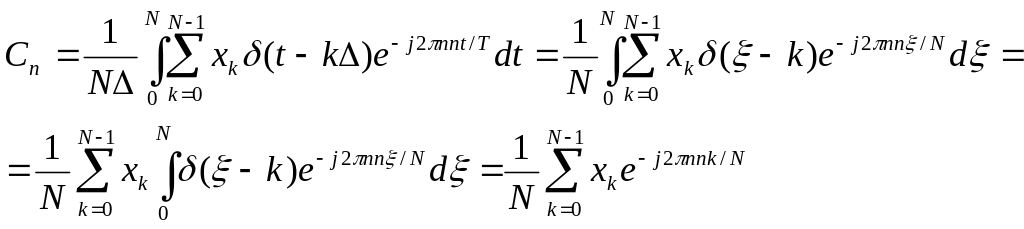

Формула (5.10) определяет последовательность коэффициентов, образующих дискретное представление Фурье (ДПФ) рассматриваемого сигнала. Его основные свойства:

1. Дискретное представление Фурье есть линейное преобразование, т.е. сумме сигналов отвечает сумма их ДПФ.

2. Число различных коэффициентов С₀,С₁,…С_N-1, вычисляемых по формуле (5.10), равно числу N отсчетов за период при n=N коэффициент С_N= С₀.

3. Коэффициент С₀ (постоянная составляющая) является средним значением всех отсчетов:

4. Если N – четное число, то:

5. Если отсчетные значения х_k – вещественные числа, то коэффициенты ДПФ, по мере которых располагаются симметрично относительно N/2, образуют сопряженные пары:

Поэтому можно считать, что коэффициенты отвечают отрицательным частотам. При изучении амплитудного спектра сигнала они не дают новых сведений.

По Коэффициентам ДПФ С₀,С₁,…С_N/2 всегда можно восстановить исходный сигнал x(t) c ограниченным спектром, который был подвергнут дискретизации. Ряд Фурье такого сигнала принимает вид конечной суммы:

, (5.11)

где - фазовый угол коэффициента ДПФ.

Восстановление непрерывного сигнала по (5.11) есть не приближенная, а точная операция, полностью эквивалентная получению текущих значений сигнала с ограниченным спектром по его отсчетам. Однако процедура, использующая ДПФ, в ряде случаев предпочтительна. Она приводит к конечным суммам гармоник, в то время как ряд Котельникова для периодического сигнала принципиально должен содержать бесконечное число членов.

Задача дискретного спектрального анализа может быть поставлена по-иному. Допустим, сто коэффициенты С_N, образующие ДПФ заданы: . Положим в выражении (5.9) t=k∆ и учтем, что суммируется лишь конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала. Таким образом, отсчетные значения могут вычисляться по формуле:

(5.12)

выражающие алгоритм обратного дискретного преобразования Фурье (ОДПФ).

Взаимно дополняющие формулы (5.10) и (5.12), чтобы вычислить ДПФ или ОДПФ последовательности из N элементов с комплексными числами. При больших массивах чисел использовать эти алгоритмы в реальном масштабе времени затруднительно. Значительно сократить число операций – до N∙log₂N – можно, используя алгоритмы быстрого преобразования Фурье. Рассматривать подробно их не будем, однако нужно помнить, что при применении БПФ число отсчетов должно быть равно N=2P.

Используя ДПФ, можно вычислить дискретную свертку двух сигналов. Если обычная свертка:

, то дискретная:

, m=0,1,2…N-1 (5.13)

Найдем связь между коэффициентами дискретной свертки и ДПФ сигналов х_д(t), y_д(t). Для этого выразим текущие значения отсчетов х_k и y_m-k как ОДПФ от соответствующих спектров:

а затем подставим эти величины в (5.13):

Изменив порядок суммирования, получим:

(5.14)

Н о =

Верхнее равенство очевидно (е^j0=0). Сумма при n≠l обращается в нуль, поскольку все слагаемые являются комплексными числами с единичным модулем и линейно нарастающим аргументом. При суммировании соответствующие векторы всегда образуют на комплексной плоскости правильный замкнутый многоугольник.

Подставив этот результат в (5.14), получим:

(5.15)

Поскольку выражение (5.15) есть ОДПФ, приходим к выводу, что коэффициенты преобразования Фурье свертки являются произведениями коэффициентов ДПФ свертываемых сигналов:

С_fk=C_xkC_yk, k=0,1,2…N-1 (5.16)

Этот результат имеет большое значение в теории дискретных сигналов и цифровых фильтров. Оказывается, что если сигналы достаточно длинны (например, содержат несколько тысяч отсчетов), то для вычисления свертки целесообразно вначале найти их ДПФ, перемножить коэффициенты, а затем воспользоваться выражением (5.15), применив алгоритм БПФ. Такой способ более экономичен, чем прямое использование формулы (5.13).