5.8 Гомоморфная обработка мультипликативного сигнала

Рассмотрим полученные результаты обработки сигнала телевизионного изображения. В этом случае условия s₁(t)>0, s₂(t)>0 не препятствуют использованию гомоморфной обработки. Дело в том, что, как правило яркость фона на экране меняется медленно, а контрастность изображения определяется высокочастотными изменениями сигнала, так что результирующий эффект можно считать пропорциональным произведению двух сигналов – низкочастотного s₁(t) и высокочастотного s₂(t). По своей природе эти сигналы являются действительными и положительными функциями времени. Примерный вид сигналов s₁(t), s₂(t) и s(t)=s₁(t)s₂(t) на рис.

Запишем эти сигналы в виде:

s₁(t)=А₀₁+∆ s₁(t)>0, s₂(t)=А₀₂+∆ s₂(t)>0,

где А₀₁ и А₀₂ – постоянные составляющие соответственно функций s₁(t) и s₂(t). Тогда:

s(t)=s₁(t)s₂(t)= А₀₁А₀₂+А₀₂∆ s₁(t)+ А₀₁∆ s₂(t)+ ∆ s₁(t) ∆ s₂(t) (5.48)

Т.к. сигнал s₁(t) меняются в широком диапазоне, соответственно меняется сигнал s(t). Это предъявляет жесткие требования к линейности амплитудной характеристики телевизионного тракта. Выгодно ослабить влияние s₁(t), от которого зависит контрастность изображения. Рассмотрим спектры сигналов.

Δ – функции описывают постоянные составляющие А₀₁ и А₀₂.

Спектр результирующего сигнала:

Произведению ∆ s₁(t) ∆ s₂(t) соответствует свертка спектров Φ_∆1(jω) и Φ_∆2(jω).

С помощью обычных линейных фильтров можно отфильтровать часть спектра в полосе от нуля до Ω. Однако спектр Φ_∆1(jω)*Φ_∆2(jω) не поддается разделению с помощью линейной фильтрации. В этих условиях эффективна гомоморфная обработка. Хотя форма колебаний х₁(t) и х₂(t) на выходе логарифмического преобразователя существенно отличается от исходных сигналов s₁(t) и s₂(t), соответствующие спектральные области разнесены на оси частот в такой же степени, что и спектры Φ_∆1(jω) и Φ_∆2(jω). В спектре

Φ₁(jω) преобладают низкие частоты, близкие к Ω, а в спектре Φ₂(jω) – частоты, нижняя граница которых близка к ω_min.

П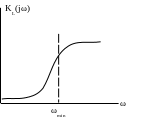 рименение линейной цепи L с АЧХ:

Позволяет существенно снизить относительный уровень низкочастотного сигнала.

После обратного нелинейного преобразования Д^-1 получается новый мультипликативный сигнал s_вых(t)=s_1вых(t)s_2вых(t) с требуемым соотношением уровней s_1вых(t) и s_2вых(t).

Таким образом можно осуществить одновременно сжатие динамического диапазона и повышение контрастности изображения.

5.9 Гомоморфная обработка свернутого сигнала

Пусть задан непрерывный сигнал s(t)=s₁(t)*s₂(t) и требуется осуществить обработку, в результате которой выходной сигнал получится также в виде свертки s_вых(t)=s_1вых(t)*s_2вых(t), но измененным соотношением между составными сигналами. В отличие от мультипликативного сигнала, в этом случае не существует подходящей функции для прямого перехода к аддитивной смеси. Можно, однако, сначала перевести операцию свертки в операцию умножения, а затем произведение преобразовать в сумму.

Подвергнув входной сигнал преобразованию Фурье, получим:

F[s(t)]=Φ(jω)=Φ₁(jω)Φ₂(jω) (5.49)

Следующий шаг – преобразование произведения в сумму с помощью выражения:

logΦ(jω)= log[Φ₁(jω)]+ log[Φ₂(jω)] (5.50)

Примени, наконец, к log[Φ(jω)] операцию обратного преобразования Фурье, мы получим аддитивные сигналы:

х₁(t)=F^-1{log[Φ₁(jω)]} и х₂(t)=F^-1{log[Φ₂(jω)]}. х(t)=х₁(t)+х₂(t).

Сигналы по своей форме естественно, существенно отличаются от исходных сигналов s₁(t) и s₂(t).

Сигнал х(t)=х₁(t)+х₂(t) подвергается линейной обработке и выходной сигнал y(t0=y₁(t)+y₂(t) преобразуется. Сначала выполняется преобразование Фурье:

Φ_y(jω)=Φ_y1(jω)+Φ_y1(jω)=F{y(t)} (5.51)

Дальнейшее преобразование вида exp[] приводит к произведению , каждый из сомножителей которого также является спектральной функцией.

Наконец, обратное преобразование Фурье:

(5.52)

определяет выходной сигнал в виде свертки, в которой сигналы s_1вых(t) и s_2вых(t) изменяются по сравнению с s₁(t) и s₂(t) в требуемом соотношении.

В практике наибольшее распространение получила гомоморфная обработка свернутого сигнала, заканчивающаяся выделением функций х₁(t) и х₂(t), содержащих всю информацию о входных сигналах s₁(t) и s₂(t).