
- •1.Технологический процесс и краткая характеристика его основных стадий (переделов)
- •2.Последовательность основных переделов в промышленности строительных материалов
- •3.Классификация основных процессов в технологии производства строительных материалов и изделий
- •5.Классификация процессов по способу организации и направленности взаимодействующих потоков
- •6. Общие принципы анализа и расчета процессов и аппаратов
- •6.1. Материальный баланс и его назначение.
- •6.2. Тепловой баланс и его назначение.
- •6.3. Интенсивность процессов и аппаратов.
- •6.4. Определение необходимой рабочей поверхности или рабочего объема непрерывно действующего аппарата.
- •6.5.Определение рабочего объема периодически действующего аппарата.
- •7. Определение условий равновесия системы: принцип Ле-Шателье и правило фаз Гиббса.
- •8.Изоморфность уравнений переноса гидродинамических, тепловых и массообменных процессов.
- •9. Основы теории подобия и моделирования систем процессов и аппаратов.
- •9.1. Основы системного анализа и понятия модели
- •9.2. Классификация моделей по в.А. Вознесенкому
- •9.4.Теоремы подобия
- •10.Механические процессы и аппараты, измельчение твёрдых материалов.
- •10.1.Силовые воздействия при измельчении материалов в машинах
- •10.2. Виды процесса измельчения материалов в зависимости от конечной крупности кусков материала.
- •10.3. Характеристики исходного и готового продукта: категории прочности и хрупкости горных пород.
- •10.4. Степень дробления
- •10.5. Основные энергетические гипотезы дробления.
- •10.6. Схемы циклов измельчения
- •11. Элементы физики твёрдого тела. Теоретическая и истинная прочность материала.
- •11.1. Дефекты реальных композиционных материалов: дефекты в кристаллах (одномерные и двумерные)
- •11.2. Теория Гриффитса разрушение твердых тел.
- •11.3. Теоретическая прочность твердых тел (формула Аравана). Критические напряжения по Гриффитсу.
- •12. Влияние среды на кинетику измельчения.
- •12.1. Эффект адсорбционного понижение прочности.
- •12.2. Кинетика измельчения и разломоспособность.
- •13. Классификация (сортировка) материалов
- •13.1. Грохочение: типы рассеивающих устройств и ситовой анализ
- •13.2. Основные схемы рассева, их достоинства и недостатки
- •3. Комбинированная схема
- •13.3. Виды грохочения, схемы механических грохотов
- •13.4.Оценка процессов грохочения (производительность и эффективность)
- •13.5.Гранулометрический состав материалов. Понятие о плотнейших упаковках.
- •14. Перемешивание материалов.
- •14.1. Эффективность аппарата и интенсивность его действия.
- •14.2. Количественная оценка качества перемешивания.
- •14.3. Классификация смесительных машин.
- •14.4. Принципиальные схемы устройств для смешивания материалов.
- •14.5.Качественные выводы на основе накопленного опыта по смешиванию материалов.
- •15. Формование изделий.
- •15.1. Коагуляционно-тиксотропные и конденсационно-кристаллизационные структуры.
- •15.2. Вибрирование. Параметры вибрации и их совокупности, определяющие качество уплотнения.
- •15.3. Разновидности вибрационных методов формования.
- •15.4. Невибрационные методы формования.
- •15.4.2. Формование с прессованием бетонной смеси. Разновидности формования с прессованием (полусухое прессование и пластическое формование).
- •16.4. Движение тел в жидкостях
- •16.5. Ламинарный режим обтекания твердого тела жидкостью. Решение (закон) Стокса для силы давления потока.
- •16.6.Турбулентный режим обтекания твердого тела жидкостью. Формула Ньютона для определения полного сопротивления.
- •16.7.Осаждение частиц под действием силы тяжести. Скорость витания частицы.
- •16.8.Движение жидкости через неподвижные и подвижные зернистые и пористые слои.
- •16.9.Определение сопротивления слоя (потери давления).
- •16.10. Гидродинамика кипящего (псевдоожиженного) слоя. Скорость и число псевдоожижения. Поршневое псевдоожижение, фонтанирование
- •16.11.Плёночное течение жидкости. Линейная плотность орошения. Принцип работы центробежного скруббера.
- •17.Барботаж. Случаи использования барботажа в промышленности строительных материалов. Пузырьковый и струйный виды работы аппарата. Принципиальная схема барботажного абсорбера.
- •17.1.Гидравлическая классификация и воздушная сепарация. Назначение.
- •17.2.Принципиальные схемы вертикального и спирального классификаторов.
- •17.3.Принцип работы проходного, циркуляционного сепараторов и циклона.
- •18.Тепловые процессы и аппараты.
- •18.1.Основные законы распространения теплоты теплопроводностью, конвекцией и излучением.
- •18.2.Сложный теплообмен: конвекцией теплопроводностью (на примере однослойной стенки).
- •18.3.Теплообмен при фазовых переходах: теплоотдача при конденсации паров. Внешний и внутренний теплообмен.
- •18.4.Движущая сила тепловых процессов. Характер изменения температур различных сред при прямоточном и противоточном движении вдоль поверхности теплообмена.
- •18.5.Теплообменные аппараты. Классификация по принципу действия, по назначению и по режиму работы. Принципиальные схемы.
- •19.Массообменные процессы: сушка
- •19.1.Способы удаления влаги и виды сушки. Классификация форм связи влаги с материалом. Статика и кинетика сушки
- •19.2.Материальный и тепловой баланс воздушной сушки
9.2. Классификация моделей по в.А. Вознесенкому
Классифицировать модели можно различными способами, которые определяются постановкой задачи. Применительно к технологии строительных материалов профессор В.А. Вознесенский предлагает классифицировать модели по признакам:

схема классификации
К модели детерминированных систем, относят такие, в которых все элементы взаимодействуют точно предвиденным способом, а случайные факторы ξ практически не влияют на течение процесса. В отличие от них модели стохастических систем подчиняются вероятностным законам. На поведение отдельных элементов таких моделей существенно влияют случайные входы.
Субстанциональные модели строят таким образом, чтобы их материал по своим свойствам был подобен материалу объекта. Например, для определения фактической прочности бетона в эксплуатируемой конструкции из нее выпиливают образец, который затем испытывают на прочность.
Структурные модели имитируют структуру или способ взаимодействия элементов объекта между собой. В промышленности строй материалов такие модели обычно строят для выявления оптимальных транспортных связей, например между ДСК (домостроительный комбинат) и строками, ДСК и поставщиками сырья.
Функциональные модели имитируют одну или несколько основных (определяющих функций объекта), например: известно что жесткость бетонной смеси является функцией концентрации С цементного теста в бетоне и истинного водоцементного отношения В/Сист.
![]()
Выявив опытным путем, вид функции f получают функциональную модель жесткости бетонной смеси.
К предметно-физическим относятся модели сохраняющие в основном природу явления. Примером может служить определение прочности бетона в конструкции выпиливанием из нее образцов являющихся одновременно и субстанциональными моделями.
Абстрактно-знаковые модели отражают взаимосвязь элементов системы с помощью дифференциальных или алгебраических уравнений, геометрических соотношений, логических операций и т.п. Частным случаем таких моделей являются математические модели широко применяемые в настоящее время. На сегодняшний день нет единой общепринятой классификации математических моделей. В различных областях их применения вводятся различные классификационные признаки.
9.3. Подобные явления. Константы и инварианты подобия, индикаторы подобия, симплексы (параметрические критерии), критерии подобия (определяющие и не определяющие), теоремы подобия, критериальные уравнения.
Теория подобия - наука о подобных явлениях.
Подобными явлениями называются системы тел, геометрически подобные друг другу, в которых протекают процессы одинаковой физической природы, и в которых одноименные причины, характеризующие явления, относящиеся между собой как постоянные числа.
Принцип выделения группы подобных явлений из класса однородных можно уяснить на следующем простом примере:
Из класса однородных аппаратов, допустим, барабанных сушилок выделяют группу подобных аппаратов отличающихся только масштабами. Если аппарат и его модель геометрически подобны, то:
![]()
![]()
где индекс 2 относится к промышленному аппарату, а 1 - к модели.
Для одной пары автоматов величина масштабного множителя С является константой геометрического подобия.
Подобия этой пары аппаратов можно выразить и другим способом по средствам инвариантов подобия.
Для рассматириваемого примера геометрического подобия можно записать:
![]()
где il - инвариант геометрического подобия представляющий собой безмерное отношение двух размеров малого барабана L1 к D1 (модели) равно отношению сходственных размеров подобного ему производственного барабана.
Инварианты подобия представляют собой выражение величины в относительных единицах. В примере один размер (длина) подобных аппаратов выражена в относительных единицах. В качестве масштаба применяют их другой пример (диаметр).
Отличие константы подобия от инварианта в том, что константа сохраняет постоянное значение во всех точках системы, но она изменяется, когда одна пара подобных явлений заменяется другой парой той же группы.
инвариант подобия наоборот различен для разных точек системы, но он не меняется при переходе от одного явления к любому другому, подобному ему, т.е. сохраняет одно и то же значение в сходственных точках всех групп подобных явлений.
Отметим еще одно свойство констант подобия: входящие в них одноименные величины могут взаимозаменяться, т.е. отношение самих величин можно заменять отношением приращений этих величин:
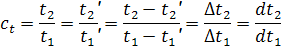
При рассмотрении сложных процессов, которые определяются многими физическими величинами выбирать произвольно константы подобия этих величин нельзя. Для этих процессов, при выборе констант подобья имеются ограничения, которые находят, исследуя уравнения описывающие процесс.
Рассмотрим правило выбора констант подобия на конкретном примере уравнений теплопроводности для плоской однородной стенки при стационарном процессе (рис ниже).
Теплопередача через однородную плоскую стенку.
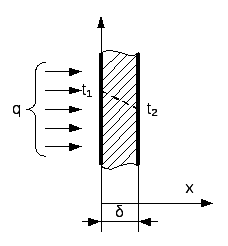
На основании закона Фурье плотность теплового потока известна и будет равна:
![]()
где q - плотность теплового потока; λ - теплопроводность материала стенки, δ - ее толщина, t1 и t2 - постоянные температуры на поверхности стенки.
Пусть первая - основная - система характеризуется значениями параметров q', λ', δ', а вторая:
![]()
![]()
![]()
Значения параметров второй системы получены путем уменьшения значения параметров первой системы на соответствующие константы подобия. Тогда для первой системы имеем:
![]()
а для второй:
![]()
разделив одно на другое получим:
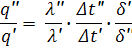
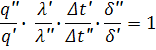
Подставляя вместо отношения величин их константы подобия:

Функции типа уравнения 1 связывающие константы подобия называются индикаторами подобия - j.
Из уровнения 1 следует весьма важный вывод: При выборе числовых значений констант подобия для группы подобных явлений необходимо соблюдение условия (j=1). Т.е. выбор значений констант условия не произволен. Требования к выбору констант подобий обусловленные уравнение 1 для рассматриваемого примера можно представить в другом, более удобном виде.
Если в указанном уравнении константу подобия представить как отношение соответствующих параметров и все уравнения с одним штрихом сгруппировать в левой части, а с двумя в правой, то:
![]()
Уравнение 2 демонстрирует основное свойство подобных явлений, заключающихся в том, что для всех подобных систем существует безразмерные комплексы величин, которые сохраняют одно и тоже значение, эти комплексы носят название инвариантов (не изменяемые) или критериев подобия. При выводе формулы 2 был рассмотрен пример, в котором основное уравнение:
![]()
задано в комплексной форме. Если основное уравнение будет задано в дифференциальной форме, то все предыдущие результаты останутся прежними, при этом как показывается в общей теории подобия для нахождения критерия подобия, необходимо в исходном уравнении отбросить все индексы, знаки суммы, символы выражающие действия дифференцирования и т.п. ибо эти упрощающие не изменяемые константы подобия.
По этому основная ценность не интерпретируемых дифференциальных уравнений (Прим: процесса конвективного теплообмена Фурье-Киргоффа, движение вязкой капельной жидкости Новье-Стокса и др.) состоит в том, что они позволяют составить критерий подобия для описываемых ими процессов.

![]()
![]()
λ - коэфициент теплопроводности, с - удельная теплоемкость, ρ - плотность.
Проведем подобные преобразования: отбросив знаки суммирования и дифференцирования:
![]()
или критерий Фурье:
![]()
полученный комплекс являетс искомым критерием подобия, который называется критерием Фурье
А при выборе констант должно выполняться условие:
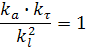
Все критерии подобия, в состав которых входит время называются критериями гомохромности, т.к. этими критериями определяется константа подобия (масштаб) времени через константы подобия других физических величин.
