Основные определения и свойства графов.

Граф G представ­ляет собой фигуру, состоящую из множества точек Х (вершин) и множества ребер U (ветвей). Каждое ребро соединяет пару ка­ких-либо вершин. Граф вида G=(X, U) может быть выражен в аналитической, геометрической или матричной форме. Каждая пара вершин графа соединена ребром. Ребро называют инцидент­ным вершине, если оно соединяет ее с какой-либо другой вершиной. Любые две вершины, связанные между собой ребром, назы­вают смежными.

Полный граф — это граф, у которого любая пара вершин со­единена ребром, в отличие от неполного графа, между некоторыми-парами вершин которого нет замыкающих ребер. Граф называют плоским, если он не имеет пересекающихся ребер, в отличие от неплоского графа, в котором таких пересечений избежать нельзя. Некоторые видимые в графе пересекающиеся ребра еще не есть пе­рекрестные, если пересечения их можно избежать соединением инцидентных им вершин ребрами в виде дуг, огибающих осталь­ные вершины У графа можно изменить порядок следования вер­шин при условии сохранения того же порядка соединения их инцидентными ребрами. Преобразованный таким образом граф на­зывают изоморфным, т. е. сходным по форме с начальным графом. Примеры геометрического построения и преобразования различ­ного вида графов приведены на рис. 2.1.

Маршрутом S называют конечную последовательность неповто­ряемых ребер. Длина маршрута определяется числом ребер и их

длиной. Цепь в графе образуется таким маршрутом, в котором нет повторяющихся ребер. Маршрут, в котором совпадают началь­ная и конечная вершины, называют циклом

С,.

Важным свойством графов является связность. Граф называют связным, если две его любые вершины связаны цепью. Множество вершин графа можно разбить на непересекающиеся компоненты связности, подграфы и суграфы. В связном графе перешейком на­зывают ребро, после удаления которого граф распадается на две компоненты связности. Образование компонентов связности упро­щает решение многих практических задач при исследовании подграфов.

Связный граф с числом вершин не менее двух, у которых соеди­нение ребер не образует ни одного замкнутого контура, называют деревом Сд. Дерево имеет только одну компоненту связности. Несвязный граф, у которого отсутствуют циклы и содержится ме­нее четырех вершин, составляет множество деревьев. Такой граф называют лесом Сд. Минимальный лес состоит из минимального числа деревьев.

Переход от электрических схем к графам и матрицам.

При решении задач конструирования РЭА машинным способом исполь­зуют абстрактные математические модели электрических схем и алгоритмы, легко поддающиеся программированию для реализа­ции на ЭВМ. В наиболее приемлемом способе перехода от элек­трических схем к графам G= (X, U) для решения задач конструи­рования элементы схемы принимаются за вершины Х= {Хi, Xj), a электрические цепи — за ребра U= (Ui, Uj).

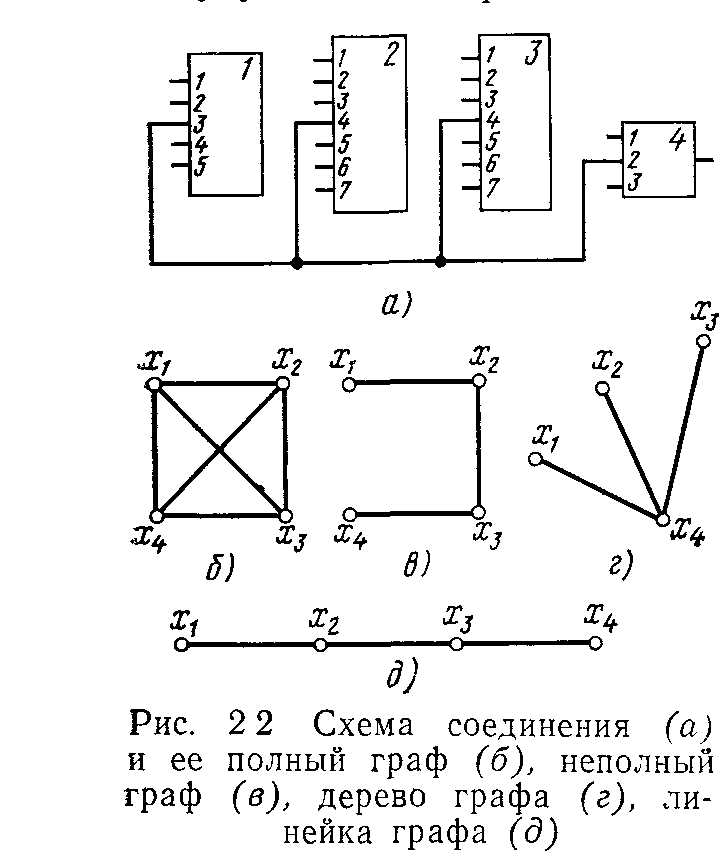
В процессе перехода от схем к графам необходимо учитывать специфику схемных элементов и предусматривать простую раз­вязку узлов электрической цепи схемы. На рис. 2.2 показаны эле­ментарная электрическая схема со­единений из четырех элементов и возможные варианты отображения ее в граф. Как видно из рис. 2.2,6, вариант в виде полного графа имеет большое число избыточных ребер, усложняющих решение задачи, по­этому стремятся использовать более простые варианты графов, показан­ные на рис. 2.2,в, г, д. Также с це­лью упрощения задачи цепи схемы, общие для всех элементов (цепи пи­тания, земля), при переходе к гра­фам не учитываются.

Принципиальные электрические схемы или схемы соединений от­дельных составляющих РЭА не со­держат замкнутых контуров и па­раллельных связей, поэтому они мо­гут быть выражены плоскими графами. Основой для прокладки' монтажных проводников служит монтажная плоскость, обычно изо­бражаемая в виде координатной сетки. Граф, нанесенный на пло­скости сетки, образует множество узлов (вершин), представляю­щих собой схемные элементы. Вершины графа соединяются наибо­лее короткими ребрами в соответствии с электрической схемой.

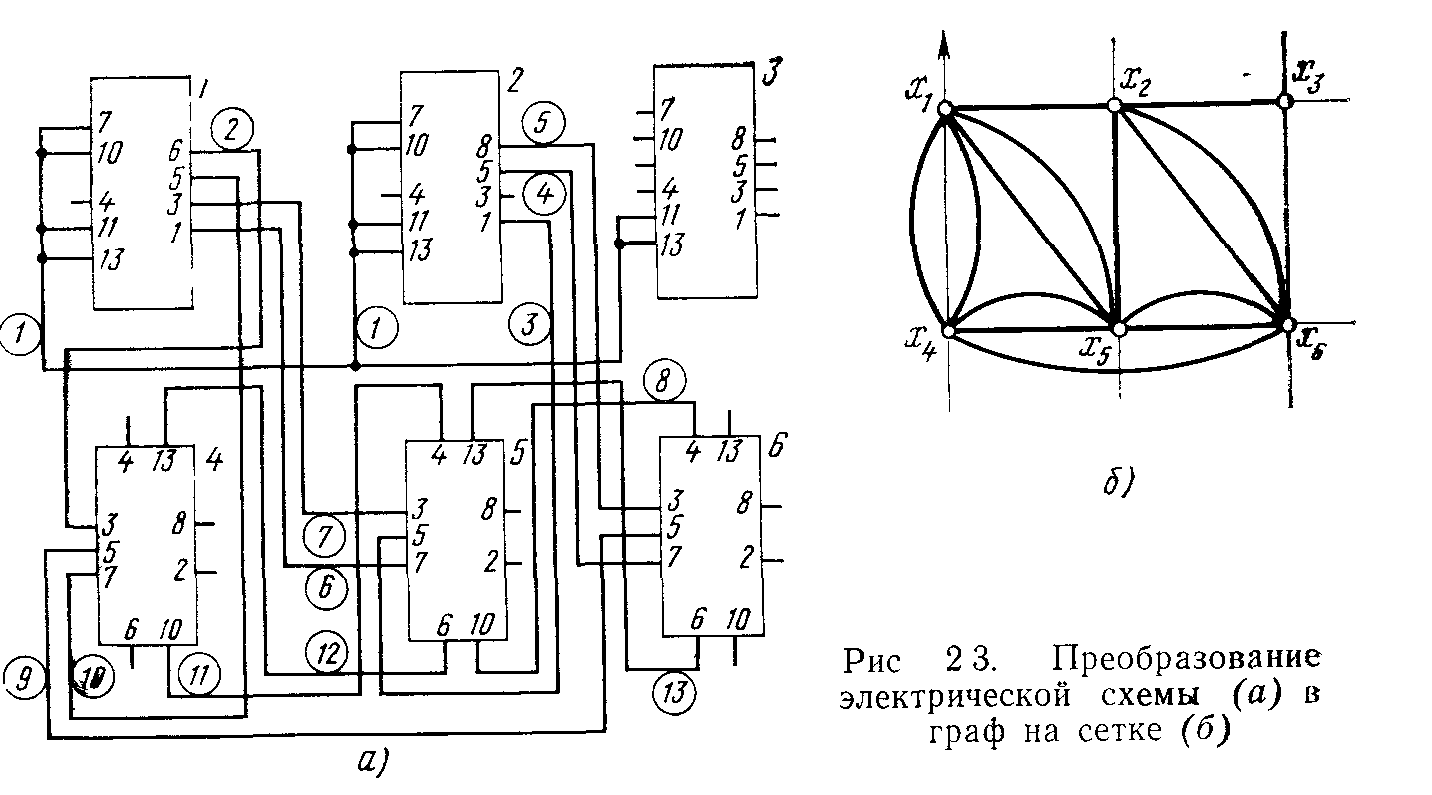
На рис. 2.3 показан пример перехода от электрической схемы к графу, выраженному в координатной сетке 1х1.

Задание графов и их формальное преобразование удобнее про­изводить с помощью матриц. Преобладающая часть известных алгоритмов конструирования работает с использованием матриц:

смежности

	X1	X2	X3	X4	X5	X6	X7	X8	X9
X1	0	2	3	1	0	0	0	5	0
X2	2	0	2	0	1	0	0	0	0
X3	3	2	0	0	3	0	0	0	3
X S= 4	1	0	0	0	0	0	3	2	0
X5	0	1	3	0	0	2	0	1	0
X6	0	0	0	0	2	0	0	3	1
X7	0	0	0	3	0	0	0	1	3
X8	5	0	0	2	1	3	1	0	2
X9	0	0	3	0	0	1	3	2	0

где 0 указывает на отсутствие соединения вершин с ребром, а остальные числа указывают на количество соединяющих ребер.

расстояний

Функция расстояний между вершинами графа.

	X1	X2	X3	X4	X5	X6	X7	X8	X9
X1	0	1	2	1	2	3	2	3	4
X2	1	0	1	2	1	2	3	2	3
X3	2	1	0	3	2	1	4	3	2
X D= 4	1	2	3	0	1	2	1	2	3
X5	2	1	2	1	0	1	2	1	2
X6	3	2	1	2	1	0	3	2	1
X7	2	3	4	1	2	3	0	1	2
X8	3	2	3	2	1	2	1	0	1
X9	4	3	2	3	2	1	2	1	0

Здесь число матрицы показывает количество связывающих вершины ребер наименьшей длины. Когда в графе задана длина ребер, то в матрице расстояний вместо количества ребер между рассматриваемыми вершинами удобнее указывать их суммарную длину. матрица расстояний напишется в виде

Матрица геометрии L графа, отображенного в решетке Gr, по­зволяет подсчитать суммарную длину его ребер. Например, матрица геометрии графа, отображенного в решетке

L=S*D=…

…………….

Качество трассировки печатных соединений зависит от того, насколько хорошо была решена задача размещения элементов на печатном поле. Выбирают такую числовую характеристику, которая обобщала бы все критерии (суммарная длина связи между элементами).

l_i- длина отдельного соединения;

n – общее количество.

************************************************************************