FOE2016

Курс: Физика конденсированного состояния

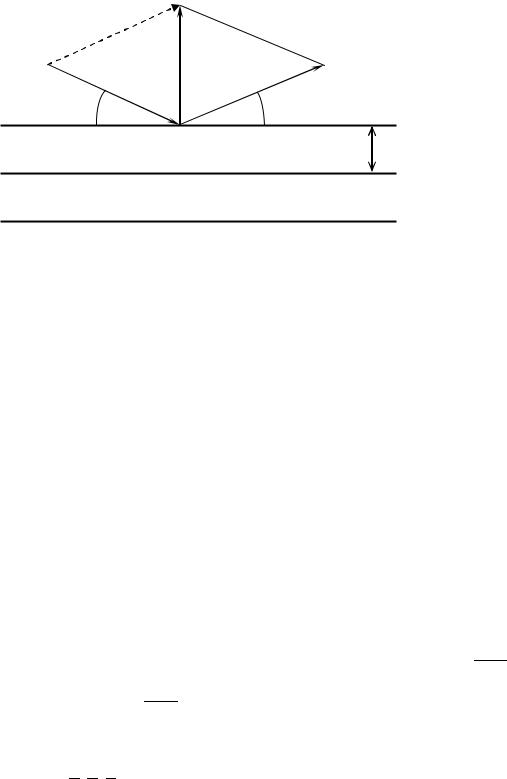
Условие дифракции можно также получить, если представить кристалл состоящим из набора параллельных атомных плоскостей, от которых происходит зеркальное отражение падающей волны (рис. 2). Дифракционный максимум в направлении отраженной волны будет наблюдаться, если разность хода для лучей 1 и 2, отраженных от соседних плоскостей, будет равна целому числу длин волн. На рис. 2 угол между направлением падающей волны и плоскостью отражения (угол падения) обозначен через , а расстояние между соседними плоскостями через d, линии АС и AD - проекции плоскости волнового фронта (поверхности постоянного значения фазы) до и после отражения. Линии АС и AD перпендикулярны, k и k’, соответственно. Из решения прямоугольных треугольников ABC и ABD можно найти разность хода l 2l 2dsin и записать условие (2) в виде

Условия Лауэ (2) и Вульфа-Брэгга (3), как будет показано ниже, эквивалентны. Поскольку вектор R, соединяющий два узла решетки, есть период решетки и может принимать дискретный набор значений (1), то из (2) следует, что при заданном волновом векторе падающей волны k, отраженная волна может распространяться в направлениях, тоже образующих дискретный набор. Обозначим вектором G изменение волнового вектора при рассеянии.

и образует бесконечную решетку, которая называется обратной решеткой. Размерность векторов обратной решетки - [длина-1]. Обратная решетка - совокупность узлов в обратном пространстве или в пространстве волновых векторов. Как и в любой решетке, в обратной решетке можно выделить векторы примитивных трансляций bi и записать произвольный вектор обратной решетки G в виде

где (h, k, l) - произвольный набор целых чисел. Чтобы условие (5) выполнялось, необходимо в качестве векторов bi выбрать векторы, связанные с элементарными трансляциями ai прямой решетки следующими соотношениями.

В этом легко убедиться, используя формулу (7) и правила вычисления произведений векторов.

2. Любой системе параллельных плоскостей прямой решетки с индексами Миллера h, k, l можно поставить в соответствие вектор Ghkl обратной решетки, перпендикулярный этим плоскостям, причем модуль вектора Ghkl связан с межплоскостным расстоянием dhkl

5

Курс: Физика конденсированного состояния

соотношением

Среди целых h, k, l не должно быть общего множителя.

3. Индексы Миллера плоскости (hkl) и вектора Ghkl, перпендикулярного им, совпадают. Индексы Миллера плоскости определяются следующим образом. Пусть плоскость отсекает

знаменателю и знаменатель отбрасывают. Тройка целых чисел, не содержащих общего множителя и есть индексы Миллера плоскости (hkl), то есть

n2 n3 : n1n3 : n1n2 h : k : l .

Вектор G, перпендикулярный плоскости (hkl), ортогонален любому вектору R, принадлежащему этой плоскости. Учитывая, что скалярное произведение (GR)=0, легко убедиться, что индексы Миллера вектора (k’)2= (k)к2 + 2kG + G2 совпадают с индексами (hkl) плоскости, ему перпендикулярной.

Закон Вульфа-Брэгга (3) и условия Лауэ (2) эквиваленты. В самом деле, из равенств (2) и

(4) следует, что

6

Курс: Физика конденсированного состояния

d h

Рис.3. Связь между векторами k, k’ и G в условиях дифракции Лауэ

Из условия Лауэ следует, что если известны направления дифракции рентгеновских лучей, то, зная длину волны падающего излучения, по ним можно восстановить часть векторов обратной решетки. Таким образом в дифракционном эксперименте непосредственно определяется обратная решетка, с которой однозначным образом связана прямая решетка.

3. Структурный фактор

Выражение (3) является лишь необходимым условием возникновения дифракционного максимума при отражении рентгеновских лучей от семейства параллельных плоскостей (hkl). Интенсивность отраженного луча зависит от величины структурного фактора S(hkl) для плоскостей (hkl), который может быть большим, малым или равным нулю. Структурный фактор зависит от форм-факторов атомов разного типа, имеющихся в кристалле, и их положений в элементарной ячейке. Базис большинства кристаллов является многоатомным. Поэтому вполне возможно, что усиленное брэгговское отражение от одной серии атомов находится в противофазе с рассеянием от других атомов базиса и будет ослабляться.

Выражение для структурного фактора при многоатомном базисе имеет вид

j 1

где fj - атомный фактор рассеяния (форм-фактор) j-гo атома базиса, rj - радиус-вектор j-того атома в элементарной ячейке, N - число атомов базиса.

Форм-фактор f зависит от порядкового номера атома Z. При малых значениях sinΘ

форм-фактор близок к Z, с увеличением sinΘ величина f уменьшается.

В качестве примера рассмотрим дифракцию на кристалле CsCl. Этому кристаллу соответствует ПК решетка, базис состоит из двух атомов, атома Cs с координатами (0,0,0) и

атома Cl с координатами a( 12 , 12 , 12) , где а - постоянная решетки. Структурный фактор S

равен

7

Курс: Физика конденсированного состояния

Если (h+k+l) - четное число, S(hkf) определяется суммой форм-факторов, то есть S=fCs + fCl, если (h+k+l) – нечетное число, то S(hkl)=fCs - fCl, то есть интенсивность дифракционного максимума будет ослаблена. Если бы форм-факторы Cs и Сl были одинаковы, то дифракционный максимум от плоскостей с индексами (h+k+l)=(2m-1) отсутствовал бы.

4. Построение Эвальда. Методы структурного анализа

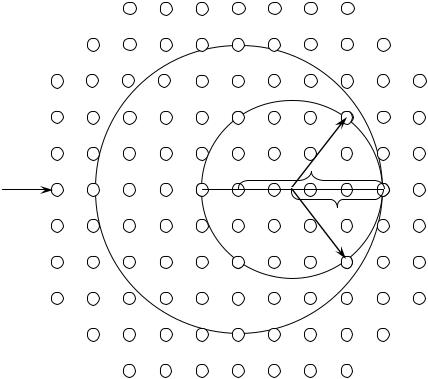
Набор векторов обратной решетки, удовлетворяющих условию Лауэ (4) при заданном векторе падающей волны k, можно определить с помощью простого геометрического построения, предложенного Эвальдом (рис. 4).

Рис.4. Геометрическое построение Эвальда

Кружки в правой части рисунка - узлы обратной решетки кристалла. Направление вектора k совпадает с направлением падающего на кристалл рентгеновского луча. Вектор k закапчивается на произвольном узле обратной решетки. На рисунке показана проекция на плоскость сферы радиуса k = 2 / с центром в начале вектора k. Дифрагированный луч образуется, если эта сфера пересекает какой-нибудь другой узел обратной решетки. Сфера, показанная на рисунке, пересекает узел, связанный с концом вектора к вектором обратной решетки G. Дифрагированный луч распространяется в направлении вектора k’= k + G. Эго построение называется построением Эвальда.

8

Курс: Физика конденсированного состояния

Проведем в обратном пространстве волновой вектор падающей волны k так, чтобы он заканчивался в произвольном узле обратной решетки. Из начала вектора k, как из центра, опишем сферу радиуса k. При этом легко видеть, что для всех узлов решетки, попавших на поверхность сферы, выполняется условие Лауэ (4), в котором вектор k’ - вектор, соединяющий центр сферы с узлом обратной решетки, лежащим на ее поверхности. Построение Эвальда позволяет дать наглядную геометрическую интерпретацию различным экспериментальным методам, используемым для определения структуры кристалла.

В методе Лауэ используется неподвижный кристалл и пучок не монохроматического излучения, с длинами волн в интервале ( min, ). Соответствующие волновые векторы лежат в интервале (k, kmax) и имеют одинаковое направление. Если провести векторы k и k’ в один и тот же узел обратной решетки и построить соответствующие им сферы Эвалъда, касающиеся в выбранном узле обратной решетки, то все векторы обратной решетки, попавшие в область, заключенную между этими сферами, будут удовлетворять условию Лауэ для какой-либо длины волны в пучке и задавать направления дифракции (рис. 5). Полученная дифракционная картина обладает полной симметрией кристалла в заданном направлении. Метод Лауэ, как правило, используется для установления ориентации кристаллов с известной структурой, симметрия которых для различных направлений известна.

Рис.5. Схема метода Лауэ в пространстве обратной решетки. Кружки - узлы обратной решетки

В методе вращающегося кристалла используется монохроматическое излучение с заданной длиной волны и вращающийся кристалл. Одновременно с поворотом прямой решетки в выбранной системе координат происходит поворот и обратной решетки. Поскольку направление k неизменно, то неизменно и положение сферы Эвальда. При вращении узлы обратной решетки описывают окружности, которые при пересечении со сферой Эвальда дают точки в обратном пространстве, указывающие направления дифракции.

9

Курс: Физика конденсированного состояния

Прост в реализации и широко используется на практике порошковый метод или метод Дебая-Шеррера, который с геометрической точки зрения аналогичен методу вращающегося кристалла, но в качестве образца используется поликристалл, состоящий из множества маленьких кристалликов, что эквивалентно набору вращений. Рассмотрим этот метод подробнее.

5. Метод порошка (метод Дебая-Шерера)

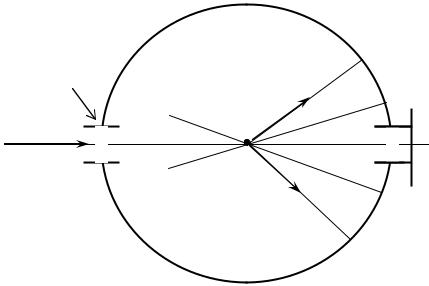
На образец, состоящий из очень большого числа маленьких кристалликов с размерами 0,01 - 0,001 мм направляется узкий пучок монохроматического рентгеновского излучения. Образец имеет форму цилиндра диаметром 0,1 - 1,0 мм и длиной 5 - 15 мм. Образцы могут быть изготовлены из проволочек или приготовляться из порошка, просеянного через сито, путем набивки его в тонкостенные капилляры из целлулоида, кварца, боролитиевого стекла. Можно, смешивая порошки с каким-либо связующим, продавливать их через капилляры и рентгенографировать после сушки. Образец помещается в центре цилиндрической рентгеновской камеры, ось которой перпендикулярна первичному пучку.

Фотопленку располагают на внутренней цилиндрической поверхности корпуса камеры. Пучок рентгеновских лучей проникает в камеру через коллиматор - оптическое устройство для получения пучков параллельных лучей. На рисунке 6 представлена принципиальная схема порошкового метода.

Рентгеновская

пленка

Рис.6. Принципиальная схема порошкового метода

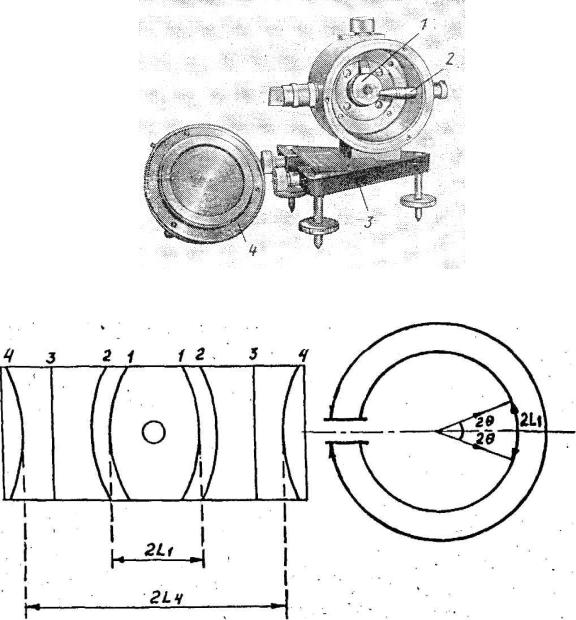
На рисунке 7 представлен общий вид цилиндрической рентгеновской камеры для получения рентгенограмм порошковым методом.

Цилиндрический корпус камеры укреплен на подставке 3, снабженной тремя установочными винтами. Ось цилиндра расположена горизонтально. Образец фиксируется в держателе 1, который закрепляется в камере на магните. Центрирование образца при установке его в держателе проводят в поле зрения микроскопа с малым увеличением. Рентгеновскую пленку крепят на внутренней поверхности корпуса, прижимая специальными распорными кольцами, закрепленными на внутренней стороне крышки камеры 4. Пучок рентгеновских лучей, омывающий образец, попадает в камеру через коллиматор 2. Так как

10

Курс: Физика конденсированного состояния

первичный пучок, попадая непосредственно на пленку позади образца, вуалирует рентгенограмму, его перехватывают по пути к пленке ловушкой. Для устранения пунктирности колец на рентгенограмме крупнокристаллического образца при съемке его вращают. Коллиматор в некоторых камерах делают так, что, вкладывая в специальные пазы спереди и сзади него свинцовые или латунные кружки (экраны) с отверстиями, можно вырезать пучок лучей круглого или прямоугольного сечения (круглая и щелевая диафрагмы). Размеры отверстий диафрагмы следует подбирать так, чтобы пучок лучей омывал образец. Обычно камеры изготавливают так, чтобы диаметр пленки в ней был кратен 57,3 мм ( т.е. 57,3; 86,0; 114,6 мм). Тогда расчетная формула для определения угла , упрощается.

Рис.7. Общий вид камеры Дебая для съемки дебаеграмм. Полученная в такой камере рентгенограмма приведена на рис. 8.

Рис.7. Схема рентгенограммы, полученной прямой съемкой в цилиндрической камере (числами указаны номера линий)

Монохроматический рентгеновский луч встречает на своем пути множество мелких кристаллов, часть из которых ориентирована так, что семейство плоскостей (hkl) в них

11

Курс: Физика конденсированного состояния

образует с рентгеновским лучом брэгговский угол , то есть находится в отражающем положении. Отраженный луч составляет угол 2 с направлением первичного луча. Поскольку в образце имеются кристаллики любой ориентации, то лучи, отраженные одним семейством плоскостей, образуют поверхность кругового конуса, осью которого является первичный луч, а угол раствора равен 4 . Каждому семейству плоскостей (hkl) соответствует конус отраженных лучей, если только межплоскостное расстояние этого семейства больше/2, то есть, если уравнение Вульфа-Брэгга дает для sin в значение меньше единицы.

Метод сводится к регистрации углов , соответствующих отражению от различных семейств параллельных плоскостей. По углу с помощью формулы Вульфа-Брэгга определяются межплоскостные расстояния для различных семейств плоскостей.

6. Исследование кристаллов кубической симметрии с атомами одного сорта

Межплоскостное расстояние dhkl в кристаллах с ПК решеткой связано с постоянной решетки а следующим соотношением.

где Qi - соответствует линии под наименьшим углом.

Если кристалл имеет кубическую симметрию и состоит из атомов одного сорта, то для него легко рассчитать структурный фактор и найти при каких h, к, l структурный фактор обращается в ноль. Так, для кристаллов с ОЦК структурой S(h,k,l)=0, если сумма (h+k+l) - нечетное число, для кристаллов с ГЦК структурой S(h,k,l)=0, если среди h, k, l есть числа разной четности. Для кристаллов со структурой типа алмаза S(h,k,l) обращается в ноль, если h, k, l. - разной четности, либо, если (h+k+1)=2(2m-1), то есть удвоенное нечетное число.

Результаты этих расчетов можно представить в виде таблицы 1.

Отметим, что для кристаллов с ПК структурой индексы (200) , (220) и (222) соответствуют максимумам 2-го порядка h, k, l.

В качестве h1, k1, l1, для ПК структуры следует выбрать индексы (100), для ОЦК индексы (110), для ГЦК и алмаза - (111). Тогда для каждой из структур можно найти ряд значений Qi и соответствующие hi, ki, li с помощью таблицы и соотношения (19). Эти значения сведены в таблице 2.

При обработке рентгенограммы по полученному ряду значений Qi и данным таблицы 2 можно определить тип структуры для кристаллов кубической симметрии и каждой линии поставить в соответствие определенные индексы Миллера h, k, l.

12

Курс: Физика конденсированного состояния

Для определения постоянной решетки следует воспользоваться соотношением (16). При

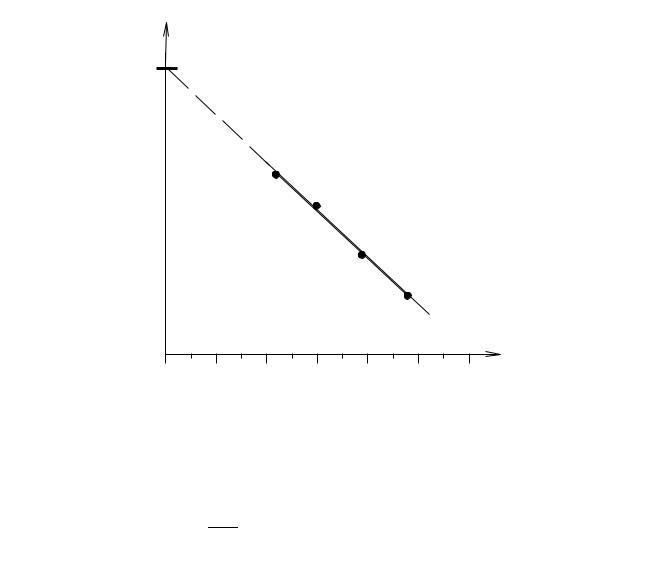
определения a следует пользоваться последними линиями. Можно воспользоваться также методом экстраполяции. Значения a находят при углах в Θ>60°, строят зависимость a = f(cos2 Θ) и экстраполируют ее до значений в Θ = π/2 (рис. 8).

13

Курс: Физика конденсированного состояния

Рис.8. Определение периода решетки кубического кристалла при помощи экстраполяции.

7. Порядок выполнения работы

1. Получить рентгенограмму у преподавателя.

2. Найти расстояния Li Dk i . 180

3. Рассчитать углы i и sin2 i, заполнить таблицу 3.

14